§22. Минимизация логических устройств

В предыдущей лекции по постановке задачи мы вывели ФАЛ и построили электронную схему, но эта схема будет трудоемкой, неэкономичной и непрактичной, поэтому необходимо минимизировать исходную функцию.

Цель минимизации

1. Уменьшение стоимости

2. Уменьшение числа внешних связей за счет увеличения внутренних

3. Регулярность или упорядоченность внутренней структцры

4. Возможность изготовления полуфабрикатов, то есть возможность решать более сложные задачи

5. Повышение надежности

Способы минимизации

1. Алгебраический метод – упрощение ФАЛ путем использования преобразований алгебры Буля

2. Кубические комплексы

3. Карты Карно

4. Метод Квайна и Мак-Класки

Рассмотрим подробнее каждый из методов

1. Итак мы вывели уравнение:

Используя правила упрощаем его

2. Кубические комплексы

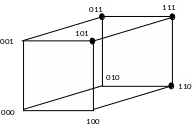
Выделяем ребра, которые целиком обозначены существующими в ФАЛ наборами. Записываем соответствующий 0-куб, включающий в себя покрытия ребер, где несовпадающее значение обозначается «_»: ((_,1,1),(1,_,1),(1,1,_)), то есть можно записать .

Если точками ограничена вся грань, то она будет описываться только одной переменной, которая совпадает во всех четырех наборах, например передняя грань, полностью описывается переменной

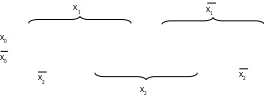
3. Карты Карно

Используются для минимизации Фал, имеющих не более 5 переменных. Карта, это прямоугольная таблица, имеющая 2ⁿ клеток, где n – это количество переменных. Рассмотрим таблицу для 3-х переменных:

В полученной таблице заменяем существующие в ФАЛ наборы единицами, несуществующие нулями, получаем следующую таблицу:

1	1 1 1	1
	1

Записываем пересечения множеств, полностью описывающих прямоугольные выделенные области. То есть получаем

4. Метод Квайна и Мак-Класки используется в автоматизированных системах для упрощения функций.

§23 Классификация логических устройств

По способу ввода-вывода информации все логические устройства делятся на:

1. Последовательные: на вход и на выход сигналы подаются поразрядно

2. Параллельные: на вход и на выход сигналы подаются и снимаются одновременно

3. Последовательно-параллельные: либо на вход поразрядно а с выхода одновременно, либо наоборот

4. Комбинационные(КЛУ): автоматы без памяти, выходные сигналы однозначно определяются только действующей в настоящий момент комбинацией на входе.

5. Последовательностные: автоматы с памятью. Сигнал на выходе определяется комбинацие сигналов на входе в данный момент времени и последовательностью комбинаций на входе в предыдущие моменты времени.

§24 Синтез логических устройств в заданном базисе

Для удобства и облегчения конструирования и эксплуатации логических схем, чаще всего при их построении используются только два элемента: Штрих Шеффера (И-НЕ) и стрелка Пирса (ИЛИ-НЕ). Это называется синтез в заданном базисе. Для перехода к заданному базису используется следующий алгоритм:

1. Применение теорем Де Моргана

2. Двойное инвертирование для применения терем Де Моргана

Синтезированная функция может содержать только заданный элемент и инвертор.

Например, задана функция, привести её к заданному базису:

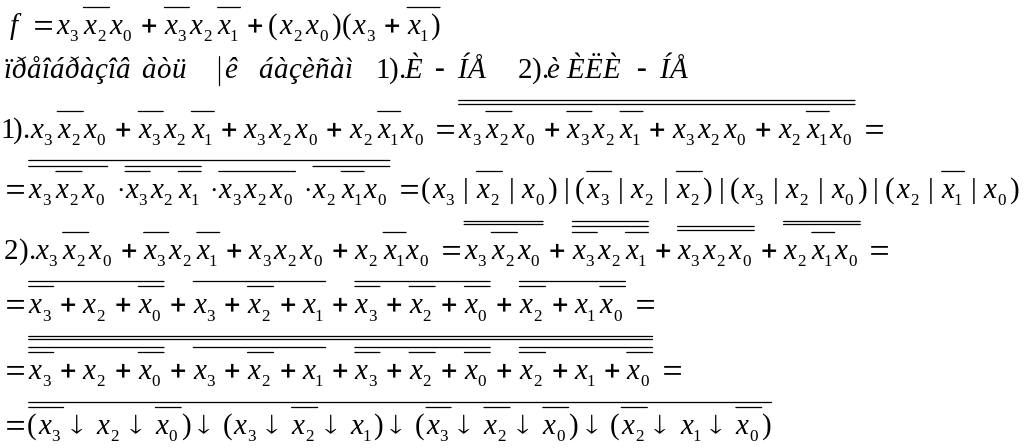(24.1)

На практике обычно задается базисный элемент и количество входов, например, 2И-НЕ, или 5ИЛИ-НЕ. Здесь может быть несколько вариантов:

1. Число входов равно количеству переменных

2. Число входов больше количества переменных

3. Число входов меньше количества переменных

Рассмотрим второй и третий случаи

2. Лишние входы необходимо изолировать, рассмотрим обобщенную таблицу истинности:

х1	х0	х1 х0	х1 + х0	х1|х0	х1↓х0
0	0	0	0	1	1
0	1	0	1	1	0
1	0	0	1	1	0
1	1	1	1	0	0

Для штриха Шеффера, «0» на входе однозначно определяет «1» на выходе, а для стрелки Пирса «1» на входе однозначно определяет «0» на выходе, следовательно:

1. Штрих Шеффера: «0» - активный логический уровень, «1» - пассивный.

2. Стрелка Пирса: «1» - активный логический уровень, «0» - пассивный

Следовательно для изоляции лишних выводов можно идти следующими путями:

1. На лишние выводы подавать пассивные логические уровни.

2. на несколько входов подавать один и тот же логический уровень, согласно правилу «х+х+…+х=х»

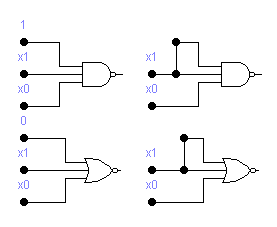
Следствия:

1. Если на все входы n-входового элемента подать одинаковый сигнал, то получим инвертор относительно n-го входа

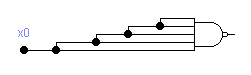
2. Если на n-1 вход n-входового элемента подать пассивный логический уровень, то получим инвертор относительно n-го входа

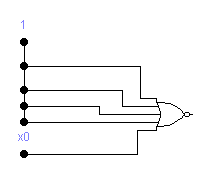
2. Если число входов больше заданного, то необходимо сократить количество переменных, здесь опять возможны два случая, когда члены исходной ФАЛ содержат общие элементы и есть возможность вынести их за скобку. И второй, когда не содержат и тогда необходимо применять специальное правило. Рассмотрим подробнее оба случая.

Первый:

Второй, применяем следующее правило: для примера рассмотрим формулу (24.1)