3. Кинетостатический расчёт

Целью кинетостатического расчёта является определение реакций в кинематических парах и равнодействующей силы давления механизма на стойку.

3.1. Силы, действующие на звенья механизма

Силы тяжести:

, отсюда ;

, отсюда ;

, отсюда ;

, отсюда .

Приложены силы тяжести в точках центров масс соответствующих звеньев и направлены вниз к центру Земли.

Силы инерции:

Сила инерции , так как роль кривошипа выполняет зубчатое колесо, центр масс которого совпадает с осью вращения .

;

;

;

.

Силы инерции приложены в точках центров масс соответствующих звеньев и направлены противоположно вектору ускорения точек центров масс этих же звеньев.

Моменты сил инерции:

Момент силы инерции , так как .

;

;

;

, так как , а следовательно и равны нулю.

Момент пары сил инерции направлен противоположно угловому ускорению звена.

Силу полезного сопротивления определим по заданному графику силы полезного сопротивления. Масштаб этого графика по оси OY будет равен:

.

.

Сила полезного сопротивления приложена в точке B и направлена противоположно вектору скорости данной точки.

3.2. Определение реакций в кинематических парах

Процесс определения реакций в кинематических парах начинаем с наиболее удалённой от ведущего звена структурной группы. Строим схему нагружения структурной группы (4;5) на чертеже в масштабе для первого положения звеньев механизма. Запишем уравнение статического равновесия:

.

В данном уравнении 4 неизвестных. Тангенциальную составляющую определим из уравнения равновесия шатуна:

, отсюда

.

Аналогичным образом найдём тангенциальную составляющую из уравнения равновесия кривошипа:

, отсюда

.

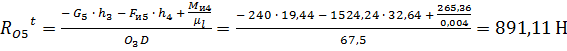Строим план сил структурной группы (4;5) в масштабе:

.

На плане сил длины векторов равны:

; ;

мм ; мм ;

; мм .

По построенному плану сил найдём неизвестные величины:

;

;

;

.

Переходим к силовому анализу следующей структурной группы (3;6). Строим схему нагружения на чертеже в масштабе для первого положения звеньев механизма. Запишем уравнение статического равновесия:

.

В данном уравнении 3 неизвестных. Тангенциальную составляющую определим из уравнения равновесия шатуна:

, отсюда

.

Строим план сил структурной группы (3;6) в масштабе . На плане сил длины векторов равны:

;

;

; .

;

По построенному плану сил найдём неизвестные величины:

;

;

.

Строим схему нагружения ведущего звена 2 на чертеже в масштабе . Силу давления шестерни на колесо определяем из уравнения равновесия ведущего звена:

, отсюда

.

Для определения реакции воспользуемся условием равновесия ведущего звена:

.

Строим план сил ведущего звена 2 в масштабе . На плане сил длины векторов равны:

; .

По построенному плану сил искомая реакция равна:

.