2.2. План скоростей

Скорость точки A определим по формуле:

V_A=ϖ₂·r=0.3·37.68=11.3м/c .

Из точки P, принятой за полюс плана скоростей, откладываем перпендикулярно к в соответствии с направлением угловой скорости вектор скорости точки A. Длину вектора выбираем так, чтобы построение плана скоростей получилось чётким и наглядным.

Пусть длина P_Va=60 . Тогда масштаб плана скоростей равен:

µ_v= = =0.18 м/с·мм.

Положение точки B на плане скоростей находи, решая систему векторных уравнений:

, где

– известный по величине и направлению вектор скорости точки A;

– неизвестный по величине, но известный по направлению вектор скорости точки B относительно точки A, направленный перпендикулярно звену AB;

– вектор скорости точки, принадлежащей стойке и равный нулю;

– неизвестный по величине, но известный по направлению вектор скорости точки B относительно стойки, направленный параллельно направляющей.

, отсюда ;

, отсюда

Положение точки C на плане скоростей найдём по изображающему свойству плана из соотношения:

, отсюда .

Скорость точки C относительно точки B:

.

Скорость точки C:

.

Положение точки D на плане скоростей находи, решая систему векторных уравнений:

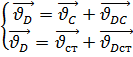, где

– известный по величине и по направлению вектор скорости точки C;

– неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки;

– вектор скорости точки, принадлежащей стойке, который равен нулю;

– неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки.

, отсюда ;

, отсюда .

Положение точки E на плане скоростей найдём по изображающему свойству плана из соотношения:

, отсюда .

Из векторного уравнения длина вектора равна:

, отсюда .

Пользуясь планом скоростей, определяем угловые скорости звеньев.

- угловая скорость кривошипа ;

, так как шатун B движется возвратно-поступательно;

- угловая скорость звена BC;

- угловая скорость звена CD;

- угловая скорость кривошипа .

2.3. План ускорений

Порядок получения точек на плане ускорений аналогичен тому, как эти точки определялись на плане скоростей. Ускорение точки A будет обладать только нормальным ускорением, величина которого равна:

.

Тогда масштаб плана ускорений будет равен:

, где мм – отрезок произвольной длины.

Направлен вектор параллельно звену из точки A в точку .

Решая систему векторных уравнений, найдём на плане ускорений положение точки B:

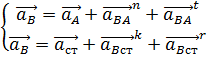, где

– нормальное ускорение точки B во вращательном движении звена AB относительно точки A, которое по модулю равно:

.

Длина отрезка равна:

мм .

– касательное ускорение точки B относительно точки A, направленное перпендикулярно к линии AB и по модулю неизвестное;

– вектор ускорения точки, принадлежащей стойке, который равен нулю;

– кориолисово ускорение точки B в движении её относительно относительно точки, принадлежащей стойке, которое равно нулю, так как направляющая этой стойки неподвижна;

– релятивное ускорение точки B относительно точки, принадлежащей стойке, параллельно направляющей стойки.

, отсюда ;

, отсюда ;

, отсюда – полное ускорение точки B относительно точки A.

Положение точки C на плане ускорений найдём по изображающему свойству плана из соотношения:

, отсюда мм .

Ускорение точки C относительно точки B равно:

Ускорение точки C равно:

.

Решая систему векторных уравнений, найдём на плане ускорений положение точки D:

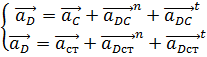, где

- нормальное ускорение точки D во вращательном движении звена DC относительно точки C, которое по модулю равно:

.

Длина отрезка равна:

.

- касательное ускорение точки D относительно точки C, направленное перпендикулярно к линии DC и по модулю неизвестное;

– вектор ускорения точки, принадлежащей стойке, который равен нулю;

- нормальное ускорение точки D во вращательном движении звена относительно точки, принадлежащей стойке, которое по модулю равно:

.

Длина отрезка равна:

.

– касательное ускорение точки D относительно точки, принадлежащей стойке, направленное перпендикулярно к звену и неизвестное по модулю.

мм , отсюда ;

, отсюда ;

, отсюда ;

, отсюда – полное ускорение точки D относительно точки C.

Положение точки E на плане ускорений найдём по изображающему свойству плана из соотношения:

, отсюда .

Из векторного уравнения длина вектора равна:

, отсюда .

Определим нормальное и касательное ускорения точки E относительно точки C:

, где

– нормальное ускорение точки E во вращательном движении звена CE относительно точки C, которое по модулю равно:

.

Длина отрезка равна:

.

– касательное ускорение точки E относительно точки C, направленное перпендикулярно к линии CE и по модулю неизвестное.

, отсюда .

Пользуясь построенным планом ускорений, определяем угловые ускорения звеньев.

, так как угловая скорость кривошипа постоянна.

, так как ползун образует поступательную пару с неподвижной направляющей стойки.

– угловое ускорение звена BC;

– угловое ускорение звена DE;

– угловое ускорение звена .