4. Основні моделі та алгоритми реалізації атракторів

4.1. Відновлення Атрактора з тимчасового ряду

Н ехай є часовий ряд експериментальних даних, що представляє собою відліки деякої фізичної величини: . Якщо відомий крок за часом , то время t=k* . Передбачається, що фізична величина s є однією з змінних динамічної системи. Система знаходиться в стаціонарному режимі, тобто фазова траєкторія проходить всередині Атрактора. Для відновлення атрактора Такенса запропоновано метод тимчасової затримки координат. У n-вимірному фазовому просторі будується послідовність точок види:

О сновний результат Такенса полягає в наступному. Якщо ,

то безліч точок задає вкладення вихідного атрактора майже при будь-якому виборі спостерігається змінної, якщо n не менш подвоєною розмірності вихідного атрактора. Для оцінки характеристик реального досліджуваного Атрактора можна обчислювати характеристики відновленого Атрактора. З метою зменшення помилки, зумовленої конечністю набору експериментальних точок

, необхідно проводити розрахунки за кількох різних значеннях M і n і домагатися незалежності одержуваних оцінок характеристик від M і n в межах заданої точності.

4 .2. Вибір тимчасової затримки

Д ля малих кроків за часом значення s i s+1 будуть близькими, тому велике значення набуває правильний вибір тимчасової затримки . Традиционный способ выбора временной задержки состоит в вычислении автокорреляционной функции временного ряда:

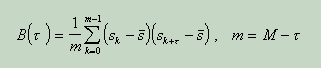
Затримка вибирається рівна часу першого перетину нуля автокореляційної функції. Другий спосіб вимагає обчислення спектру потужності тимчасового ряду, тобто швидкого перетворення Фур'є автокореляційної функції. Якщо в спектрі потужності присутні кратні піки, то затримка вибирається рівної чверті періоду найвищою з домінуючих частот. Третій спосіб заснований на обчисленні середньої взаємної інформації між двома вимірами. Нехай дано дві множини вимірювань A і B. Взаємна інформація між елементом ai безлічі A і елементом bj множини B визначається як кількість інформації, яку мають вимірювання ai і bj по відношенню до один одного:

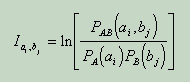
Якщо вимірювання незалежні, то взаємна інформація дорівнює нулю. Усереднюючи по всіх вимірах, отримуємо:

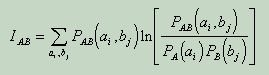
4.3. Алгоритм обчислення кореляційної розмірності атрактора

У разі модельних даних, коли нам відома розмірність n фазового простору динамічної системи і всі n координат кожної точки на Атракторі, кореляційна розмірність D2 Атрактора знаходять наступним чином: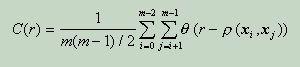

У разі експериментальних даних ми зазвичай не знаємо розмірність фазового простору системи і володіємо інформацією тільки про одну координаті точок на Атракторе. Тому всі розрахунки проводяться для декількох розмірностей фазового простору n = 1,2,3, ... Для відновлення атрактора використовується метод Такенса. При цьому кореляційний розмірність Атрактора D2 (n) спочатку зростає, але потім зазвичай виходить на постійний рівень. Таким чином, отримують шукану кореляційну розмірність D Атрактора і оцінку розмірності фазового простору системи. Якщо ж вихідний сигнал динамічної системи сильно зашумлен, то розмірність Атрактора постійно зростає.

4.4. Алгоритм обчислення кореляційної ентропії Атрактора

К ореляційна ентропія K може бути обчислена досить просто. Для цього також обчислюють кореляційний інтеграл, але розглядають не тільки його залежність від відстані r, а й від розмірності фазового простору n. При цьому вважають, що