3. Дивні атрактори. Основні види атракторів
Дивний Атрактор - це Атрактор, що має дві істотні відмінності від звичайного Атрактора: траєкторія такого атрактора неперіодична (вона не замикається) і режим функціонування нестійкий (малі відхилення від режиму наростають). Основним критерієм хаотичності Атрактора є експоненціальне наростання в часі малих збурень. Наслідком цього є «перемішування» у системі, неперіодичних в часі будь-який з координат системи, суцільний спектр потужності і спадаючий в часі автокореляційна функція.Динаміка на дивних Атракторах часто буває хаотичної: прогнозування траєкторії, що потрапила в Атрактор, утруднене, оскільки мала неточність у початкових даних через деякий час може призвести до сильного розбіжності прогнозу з реальною траєкторією. Непередбачуваність траєкторії в детермінованих динамічних системах називають динамічним хаосом, відрізняючи його від стохастичного хаосу, що виникає в стохастичних динамічних системах. Це явище також називають ефектом метелика, маючи на увазі можливість перетворення слабких турбулентних потоків повітря, викликаних помахом крил метелика в одній точці планети в потужне торнадо на іншій її стороні внаслідок багаторазового їх посилення в атмосфері за деякий час.Серед дивних атракторів зустрічаються такі, хаусдорфова розмірність яких відмінна від топологічної розмірності і є дробової. Одним з найбільш відомих серед подібних атракторів є Атрактор Лоренца.
3.1. Атрактор Лоренца
А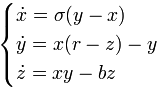
трактор
Лоренца (від англ. To attract - притягати) -
компактне інваріантне безліч в
тривимірному фазовому просторі гладкого
потоку, яке має певну складну топологічну
структуру і є асимптотично стійким,
воно стійко за Ляпуновим і всі траєкторії
з деякої околиці прагнуть до при (звідси
назва). Атрактор Лоренца був знайдений
в чисельних експериментах Лоренца, що
досліджував поведінку траєкторій
нелінійної системи:
при наступних значеннях параметрів: σ = 10, r = 28, b = 8/3. Ця система спочатку була введена як перша нетривіальне галеркінское наближення для задачі про конвекції морської води в плоскому шарі, чим і мотивувався вибір значень σ, r і b, але вона виникає також і в інших фізичних питаннях і моделях:
конвекція в замкнутій петлі;
обертання водяного колеса;
модель одномодового лазера;дисипативний осцилятор з інерційною нелінійністю.
В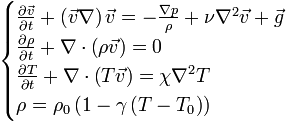
ихідна
гідродинамічна система рівнянь:
Варто вказати, що стосовно до задачі про конвекції модель Лоренца є дуже грубим наближенням, дуже далеким від реальності. Більш-менш адекватне відповідність існує в області регулярних режимів, де стійкі рішення якісно відображають експериментально спостережувану картину рівномірно обертових конвективних валів (Осередки Бенара). Хаотичний режим, притаманний моделі, не описує турбулентної конвекції в силу істотної обрізки вихідних тригонометричних рядів.Цікавим є істотно велика точність моделі при деякій її модифікації, застосовувана зокрема для опису конвекції в шарі, що піддається вібрації у вертикальному напрямку або змінному тепловому впливу. Такі зміни зовнішніх умов призводять до модулювання коефіцієнтів в рівняннях. При цьому високочастотні Фур'є-компоненти температури і швидкості істотно придушуються, покращуючи відповідність моделі Лоренца і реальної системи.
Програми, що моделюють поведінку системи Лоренца:
BASIC
DIM x, y, z, dt, x1, y1, z1 AS SINGLE
DIM a, b, c AS INTEGER
x = 3.051522: y = 1.582542: z = 15.62388: dt = 0.0001
a = 5: b = 15: c = 1
SCREEN 12
PRINT "Press Esc to quit"
WHILE INKEY$ <> CHR$(27)
x1 = x + a * (-x + y) * dt
y1 = y + (b * x - y - z * x) * dt
z1 = z + (-c * z + x * y) * dt
x = x1
y = y1
z = z1
PSET ((19.3 * (y - x * .292893) + 300), (-11 * (z + x * .292893) + 360)), 9
WEND
END
HTML5
<html>
<body>
<canvas height='500' width='500' id='cnv'></canvas>
<script>
var cnv = document.getElementById("cnv");
var cx = cnv.getContext('2d');
var x = 3.051522, y = 1.582542, z = 15.62388, x1, y1, z1;
var dt = 0.0001;
var a = 5, b = 15, c = 1;
var h = parseInt(cnv.getAttribute("height"));
var w = parseInt(cnv.getAttribute("width"));
var id = cx.createImageData(w, h);
var rd = Math.round;
var idx = 0;
i=1000000; while (i--) {
x1 = x + a*(-x+y)*dt;
y1 = y + (b*x-y-z*x)*dt;
z1 = z + (-c*z+x*y)*dt;
x = x1; y = y1; z = z1;
idx=4*(rd(19.3*(y - x*0.292893) + 320) + rd(-11*(z + x*0.292893) + 392)*w);
id.data[idx+3] = 255;
}
cx.putImageData(id, 0, 0);
</script>
</body>
</html>
3.2. Соленїд Смейла-Вільямса
Соленоїд Смейла - Вільямса - приклад оборотної динамічної системи, аналогічної з поведінки траєкторій відображенню подвоєння на колі. Більш точно, ця динамічна система визначена на полноторіі, і за одну її ітерацію кутова координата подвоюється; звідки автоматично виникає експоненціальне розбігання траєкторій і хаотичність динаміки. Також соленоидом називають і максимальний Атрактор цієї системи (звідки, власне, і походить назва): він влаштований як (незліченну) об'єднання «ниток», намотуються вздовж полноторія.
Відображенням соленоїда називають відображення
п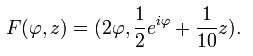
олноторія
в себе, задане як
Тут диск для зручності розглядається як одиничний диск на комплексній площині:
3.3. Атрактор Пликіна
Атрактор Пликіна — приклад динамічної системи на диску, максимальний атрактор якої гіперболічний. Зокрема, цей приклад структурно стійкий, як відповідний аксіомі A Смейла.
Конструкція
А
трактор
Пликіна будується як фактор дифеоморфізма
тора, що є DA-Дифеоморфізм. А саме,
дифеоморфізм Аносова
зберігає точки , які є нерухомими для відображення I: x \ mapsto-x. Більш того, можна провести DA-конструкцію, побудувавши коммутирующий з I Дифеоморфізм f, для якого ці точки стають відразливими, причому відображення в околиці цих точок є чистою (розтягує) гомотетія.
Фактор тора по дії інволюції I — це двовимірна сфера (а відповідне накриття — дволистою з розгалуженням у чотирьох точках), і комутуючий з I відображення f спускається до Дифеоморфізм сфери з чотирма відразливими нерухомими точками. Перенесення одного з них на нескінченність (що дозволяє перейти до відображення диска в себе) закінчує побудова прикладу Пликіна.