§ 5. Современное развитие геодезии

В последние десятилетия стремительный технический прогресс и внедрение новой вычислительной техники привели к появлению новых методов и технологий в обработке результатов геодезических измерений. Появились новые направления в картографировании и создании карт. Сегодня геодезия - это, по большей части, спутниковая геодезия, основанная на системах ОР8 (США) и ГЛОНАСС (РОССИЯ). Трудно представить современную геодезию без тесного взаимодействия с аэрокосмическим зондированием, геоинформатикой. Электронные карты и атласы, трехмерные картографические модели и другие геоизображения стали привычными средствами исследования для геодезистов и других специалистов в науках о Земле.

Глава II. Определение положения точек земной поверхности относительно общей фигуры земли

§ 6. Общая фигура и размеры Земли

Положение точек земной поверхности обычно определяют относительно обшей фигуры Земли. Под общей фигурой Земли в геодезии понимают фигуру, ограниченную мысленно продолженной поверхностью океанов, находящихся в спокойном состоянии. Такая замкнутая

поверхность в каждой своей точке перпендикулярна к отвесной линии, т. е. к направлению действия силы тяжести и, следовательно, всюду горизонтальна. Ее называют уровенной поверхностью

Величина а

Земли или поверхностью геоида. Геоид - тело, не имеющее правильной геометрической формы. Однако поверхность геоида ближе всего подходит к поверхности эллипсоида вращения, получающегося от вращения эллипса Р0Р^1 (рис. 1) вокруг малой оси РР_Ь Поэтому практически при геодезических и картографических расчетах поверхность геоида заменяют математической поверхностью эллипсоида вращения, называемого также сфероидом. Линии пересечения поверхности сфероида плоскостями, проходящими через ось вращения, называются меридианами и представляются на сфероиде эллипсами, а линии пересечения плоскостями, перпендикулярными к оси вращения, называются параллелями и являются окружностями. Параллель, плоскость которой проходит через центр сфероида, называется экватором. Линии О0=а и ОР=Ь (рис. 1) называются большой и малой полуосями сфероида; а - радиус экватора, Ь - полуось вращения Земли. Размеры земного сфероида определяются длинами этих полуосей.

а - Ъ

называется сжатием сфероида. Величины а, Ь, а могут быть определены

а

посредством градусных измерений, которые позволяют вычислить длины дуги меридиана в 1°. Зная длину градуса в различных местах меридиана, можно установить фигуру и размеры Земли.

Размеры земного сфероида и его сжатия определялись неоднократно учеными разных стран.

С 1946 г. для геодезических и картографических работ в России приняты размеры земного сфероида Красовского

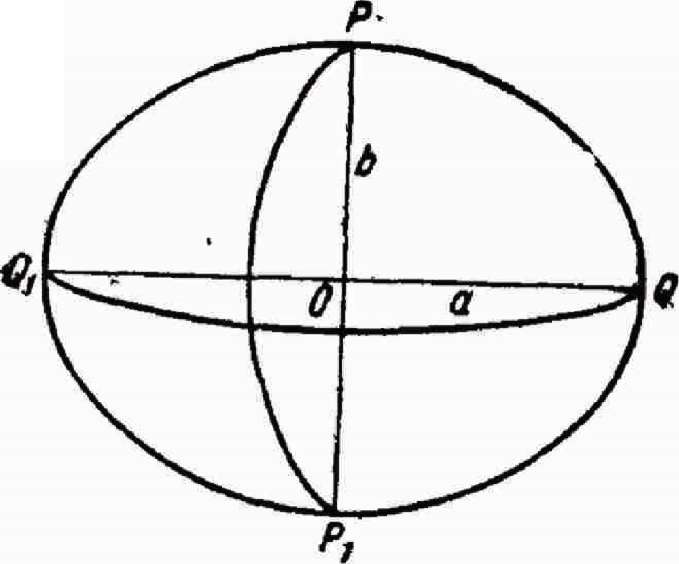
Рис. 1

а=6 378 245 м, Ъ =6 356 863 м, а =1:298,3.

Сжатие земного сфероида составляет приблизительно 1:300. Если представить себе глобус с большой полуосью а =300 мм, то разность а - Ь для такого глобуса составит всего 1 мм. Ввиду малости сжатия общую фигуру Земли иногда принимают приближенно за шар радиуса К=6371 км.