Методы финансовых вычислений

Финансовые вычисления, базирующиеся на понятии временной стоимости денег, являются одним из элементов финансового анализа и используются в различных его разделах. Наиболее интенсивно они применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудозаемных операциях, в оценке бизнеса и др. К ним относятся, в первую очередь, методы наращения и дисконтирования, методы оценки денежных потоков и методы оценки доходности.

В любой финансовой операции присутствуют величины, которые заданы, а одна является искомой. Например, на счет в банк кладется определенная сумма денег и известна ставка банковского процента по вкладам, а также срок вклада, и требуется определить, какая сумма будет получена в результате этой операции. Или наоборот, известно, какая сумма денег нужна в будущем, а также известна ставка, под которую можно сегодня положить деньги в банк, чтобы приумножить их. Требуется определить, какую сумму нужно вложить, чтобы получить в будущем желаемую сумму.

Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется процессом наращения, искомая величина в этом случае – наращенная в результате операции сумма, а используемая в операции ставка называется ставкой наращения. Для начисления процентов используются схемы простых или сложных процентов. Процесс, в котором заданы ожидаемая в будущем к получению (наращенная) сумма и ставка, называется процессом дисконтирования. Искомая величина в такой задаче – исходная сумма, которую нужно вложить, чтобы получить в будущем заданную сумму. Она называется приведенной суммой, а используемая в операции ставка – ставкой дисконтирования. Операции вычисления наращенной или приведенной суммы называют операциями наращения и дисконтирования.

В практике деятельности хозяйствующих субъектов часто встречаются финансовые контракты, предусматривающие не единичные выплаты в начале и в конце срока действия контракта, а серии последовательных выплат. Такие периодические выплаты (или поступления) называются денежными потоками (аннуитетами). Наглядным примером денежного потока является получение с определенной периодичностью процентов по процентным облигациям. Расчеты финансовых характеристик денежных потоков обобщенно называют методами оценки денежных потоков (аннуитетов).

Существенной характеристикой всех финансовых инструментов (ценных бумаг, банковских вкладов и т. д.) является их доходность. Формулы расчета доходности при разных условиях составляют метод оценки доходности. Например, различают доходность акций к продаже и текущую (дивидендную) доходность.

Экономико-математические методы

Самым современным и динамично развивающимся направлением экономического анализа являются экономико-математические методы (ЭММ). Эти методы позволяют существенно повысить точность и скорость проведения анализа, а также решать задачи со многими неизвестными. Применение экономико-математических методов требует от аналитика сильной математической подготовки, обеспеченности его компьютерной техникой и соответствующим программным обеспечением.

Использование ЭММ обеспечивает решение сложнейших многовариантных аналитических задач в режиме реального времени. Например, рабочее место любого трейдера фондового рынка оснащено программным пакетом ЭММ (в основном математико-статистических), позволяющих за доли секунды прогнозировать будущие изменения курса и объемов торговли ценными бумагами по информации о ценах и объемах ранее состоявшихся сделок. Такое программное обеспечение стоит от нескольких десятков до нескольких сотен тысяч долларов.

Дороговизна внедрения ЭММ является одной из основных причин недостаточного их использования в практике анализа на российских предприятиях и в организациях.

К ЭММ относятся, в частности:

– методы теории принятия решений;

– методы математической статистики;

– эконометрические методы;

– методы исследования операций;

– методы экономической кибернетики.

Теория принятия решений включает следующие методы:

– методы ситуационного анализа и прогнозирования, в том числе методы построения дерева решений;

– методы имитационного моделирования;

– анализ чувствительности.

Метод построения дерева решений входит в систему методов ситуационного анализа и используется в случаях, когда прогнозируемая ситуация может быть структурирована таким образом, что выделяются ключевые моменты, в которых либо нужно принимать решение с определенной вероятностью (роль аналитика или менеджера активна), либо, также с определенной вероятностью, наступает некоторое событие (роль аналитика или менеджера пассивна, однако значимы некоторые не зависящие от его действий обстоятельства). Именно для формализованного описания подобных ситуаций и используется метод построения дерева решений.

Рассмотрим логику метода на примере. Управляющему нужно принять решение о целесообразности приобретения либо станка Ml, либо станка М2. Станок М2 более экономичен, что обеспечивает больший доход на единицу продукции, вместе с тем, он более дорогой и требует относительно больших накладных расходов (см. табл. 4.18).

Таблица 4.18

Данные о станках

Наименование	Накладные расходы, руб.	Операционный доход на единицу продукции, руб.
Станок М1	15000	20
Станок М2	21000	24

Процесс принятия решения может быть выполнен в несколько этапов.

Этап 1 – определение цели. В качестве критерия выбирается максимизация математического ожидания прибыли.

Этап 2 – определение набора возможных действий для рассмотрения и анализа (контролируются лицом, принимающим решение). Управляющий может выбрать один из двух вариантов:

1) a₁ = {покупка станка Ml};

2) a₂ = {покупка станка М2}.

Этап 3 – оценка возможных исходов и их вероятностей (исходы носят случайный характер). Предположим, управляющий оценивает возможные варианты годового спроса на продукцию и соответствующие им вероятности следующим образом:

x₁ = 1200 единиц с вероятностью 0,4;

x₂ = 2000 единиц с вероятностью 0,6.

Этап 4 – оценка математического ожидания возможного дохода. Выполняется с помощью дерева решений (рис. 4.1).

Из приведенных на схеме данных можно найти математическое ожидание возможного исхода по каждому проекту:

(руб.);   

(руб.).

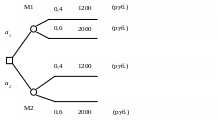
Рис. 4.1. Дерево решений

Таким образом, вариант с приобретением станка М2 является экономически более целесообразным.

Метод построения дерева решений весьма полезен в различных областях деятельности менеджеров, например, в управленческом учете, при составлении бюджета капиталовложений и особенно в анализе на рынке ценных бумаг.

Анализ чувствительности. В условиях неопределенности никогда нельзя точно определить заранее, каковы будут фактические значения той или иной величины через определенное время. Однако для успешного планирования, например, производственной деятельности следует предусмотреть изменения, которые могут произойти в будущем с ключевыми для этой деятельности экономическими показателями, например, изменение цен на сырье и на конечную продукцию предприятия, а также возможное падение или увеличение спроса на товары, производимые предприятием. Для этого выполняется аналитическая процедура, называемая анализом чувствительности. Очень часто этот метод используется при анализе инвестиционных проектов, а также при прогнозировании величины чистой прибыли предприятия. Анализ чувствительности заключается в определении того, что будет, если один или несколько факторов изменят свою величину. Анализ одновременного изменения нескольких факторов выполнить вручную практически невозможно, это позволяет сделать компьютер. Анализ чувствительности также позволяет определить силу реакции результативного показателя на определенное изменение факторов.

Методы математической статистики включают:

– корреляционный анализ;

– регрессионный анализ;

– дисперсионный анализ;

– кластерный анализ;

– методы современного факторного анализа;

– методы обработки пространственно-временных совокупностей.

Корреляционный анализ есть метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону. Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Возникать корреляционная связь может несколькими путями. Важнейший из них – причинная зависимость вариации результативного признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин.

Регрессионный анализ – это метод установления аналитического выражения (формулы) стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется результативный показатель при изменении любого из факторных показателей. В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов то регрессионный – одностороннюю зависимость, то есть связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный. Регрессионный анализ – один из наиболее разработанных методов математической статистики.

Дисперсионный анализ – это статистический метод, позволяющий подтвердить или опровергнуть гипотезу о том, что две выборки данных относятся к одной генеральной совокупности. Применительно к анализу деятельности предприятия можно сказать, что дисперсионный анализ позволяет определить, к одной и той же совокупности данных или нет относятся группы разных наблюдений. Дисперсионный анализ часто используется совместно с методами группировки. Задача его проведения в этих случаях состоит в оценке существенности различий между группами.

Кластерный анализ – один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве.

Методы современного факторного анализа. В эту группу входят методы анализа многофакторных зависимостей в условиях, когда факторы существенно коррелируют между собой. Дело в том, что практическое применение классических регрессионных моделей в экономическом анализе сопряжено с необходимостью преодоления ряда трудностей, основная из которых – мультиколлинеарность факторов. Особенность объектов экономического анализа заключается в тесной взаимосвязи и взаимообусловленности показателей, поэтому бездумное и необоснованное включение в регрессионную модель бессистемно отобранных показателей нередко приводит к искусственности модели, невозможности ее использования на практике. Если пытаться следовать формальным требованиям регрессионного анализа в полном объеме, то, например, устранение мультиколлинеарности нередко сводится к отбрасыванию существенно коррелирующих факторов. В этом случае, во-первых, имеет место потеря информации и, во-вторых, анализ чаще всего выхолащивается, в некотором роде теряет смысл, поскольку модель сводится к одно- или двухфакторной.

Особенность современного факторного анализа заключается в том, что он дает возможность совместной обработки большого числа взаимосвязанных (коррелирующих) факторов. Аппарат современного факторного анализа позволяет свести десятки исходных признаков (факторов) к нескольким обобщенным, которые не наблюдаются непосредственно при исследовании, но, тем не менее, появляются в модели как линейные комбинации исходных факторов и поддаются определенной интерпретации. Важная особенность подобных обобщенных факторов состоит в том, что они не коррелируют между собой, и потому их удобно использовать для построения уравнения регрессии.

Методы современного факторного анализа предназначены для решения следующих задач:

– отыскание скрытых, но объективно существующих закономерностей между факторами и оценка их влияния на результативные показатели;

– описание изучаемого явления значительно меньшим числом обобщенных факторов (например, исходных факторов было 20, а обобщенных – 3–4, но они объемлют информацию всех или почти всех исходных факторов);

– выявление стохастической связи между исходными и обобщенными факторами (например, зависимость между обобщенным фактором «технический уровень предприятия» и частными факторами, его образующими: фондовооруженностью, фондообеспеченностью и др.);

– построение уравнения регрессии на обобщенных факторах (в качестве результативного показателя может использоваться, например, некоторый показатель эффективности финансово-хозяйственной деятельности).

Наибольшее распространение среди методов данной группы получили два: метод главных компонент и собственно современный факторный анализ.

Методы обработки пространственно-временных совокупностей показателей. В ходе экономического анализа зачастую приходится сталкиваться с информационными массивами в виде совокупностей показателей. В общем виде они подразделяются на три группы:

– временная, то есть ряд динамики (например, динамика доходности акций некоторой компании, динамика запасов товарно-материальных ценностей и др.);

– пространственная, то есть совокупность показателей по группе объектов на определенную дату или за определенный период (например, данные о товарообороте за некоторый период по ряду предприятий);

– пространственно-временная, то есть совокупность показателей по группе объектов за ряд периодов (например, данные о доходности облигаций нескольких эмитентов в динамике за несколько периодов). Очевидно, что данный тип совокупности показателей обобщает два предыдущих.

Техника аналитической обработки информационных массивов для первых двух ситуаций достаточно проработана и сводится чаще всего к корреляционно-регрессионному анализу. Что касается последней ситуации, то она более сложна как в техническом, так и в процедурном планах. Аналитическая обработка подобных информационных массивов осуществляется с помощью специальных методов, которые условно называют статистическими методами обработки пространственно-временных совокупностей показателей.

К эконометрическим методам относятся, в частности:

– метод производственных функций;

– метод межотраслевого (межпродуктового) баланса.

Методы исследования операций включают:

– методы математического программирования;

– методы управления запасами;

– методы теории игр;

– методы теории расписаний;

– сетевые методы планирования и управления;

– методы теории массового обслуживания.

Методы математического программирования в экономическом анализе используются для оптимизации показателей. Термин «программирование», вошедший в отечественную экономическую литературу в 60-е годы XX в., имеет несколько значений. Во-первых, этим термином обозначается процесс разработки специальной программы для ЭВМ; во-вторых, он используется как некоторый синоним терминов «планирование» и «прогнозирование». В последнем случае обычно говорят об оптимальном программировании, понимая под этим методы разработки планов и программ, позволяющих оптимизировать некоторые стороны деятельности хозяйствующего субъекта. Особенность методов оптимального программирования заключается в активном использовании достаточно сложных экономико-математических методов.

Математическое программирование – это раздел математики, в котором описаны методы нахождения минимума или максимума функции нескольких переменных при заданном наборе ограничений. Он включает несколько разделов, различающихся разной степенью сложности, проработанности и практической применяемости, в том числе линейное программирование. Линейное программирование чаще других применяется в прикладных экономических исследованиях ввиду его относительной простоты и достаточно наглядной интерпретации. Линейным программированием этот раздел называется потому, что он посвящен исследованию линейных функций при заданных линейных ограничениях. С помощью линейного программирования в анализе финансово-хозяйственной деятельности решается целый ряд задач, в первую очередь относящихся к процессу планирования деятельности, этот метод позволяет отыскивать оптимальные параметры выпуска продукции и способы наилучшего использования имеющихся ресурсов.

Без использования линейного программирования руководитель может рассмотреть несколько разработанных его специалистами планов и выбрать тот, который наилучшим образом удовлетворяет поставленной цели. Но не факт, что это будет самый оптимальный вариант. Суть метода линейного программирования заключается в поиске максимума или минимума целевой функции при имеющихся ограничениях с помощью численных методов (в частности, с помощью симплекс-метода), которые позволяют перебрать все возможные варианты и выбрать действительно лучший. Рассмотрим использование этого метода на примере.

Фабрика по производству чая выпускает две марки этого продукта. Условное наименование марок – А и В. Отпускная цена чая марки А – 60 руб. за килограмм, марки В – 50 руб. за килограмм. Каковы должны быть оптимальные годовые объемы производства чая обеих марок, чтобы выручка фабрики от их реализации была максимальной?

Пусть оптимальный объем производства чая марки А составит x т в год, а марки В – у т в год. Суммарная выручка от их реализации составит (60х + 50у) руб. Решение задачи подразумевает поиск такой комбинации (х, у), которая позволила бы обеспечить максимум этой функции, то есть поиск

Понятно, что чем больше будет выпуск и той, и другой марки, тем больше будет выручка, однако ресурсы фабрики небезграничны. Для изготовления обоих сортов чая используется одно и то же оборудование, общая производительность которого составляет 300 т продукции в год. Таким образом, ограничение по мощности оборудования выглядит следующим образом:

.

При изготовлении чайных смесей разных марок используют чайный лист двух сортов: в состав чая марки А входит 70 % первого сорта и 30 % второго сорта, в состав марки В – 20 % первого сорта и 80 % второго сорта. Стоимость сырья первого сорта составляет 38 руб. / кг, второго сорта – 24 руб. / кг. Таким образом, себестоимость чайного листа, необходимого для производства одного килограмма чая марки А, составляет 33,8 руб.:

а марки В – 26,8 руб.:

Фабрика может потратить на закупку сырья не более 9000 тыс. руб. в год. Следовательно, на объем выпуска накладывается еще одно ограничение финансового порядка:

33,8х + 26,8у  9000.

Понятно, что искомые величины объемов производства разных сортов чая (х и у) должны быть положительны. Таким образом, полная формулировка задачи линейного программирования в данном случае будет следующей:

Найденное с помощью симплекс-метода решение этой системы уравнений будет таким:

.

Именно такое соотношение объемов выпуска чая сортов А и В позволит фабрике при существующих технологических и финансовых ограничениях получить максимальный объем выручки.

Ограничения в задачах линейного программирования могут касаться не только технологических и финансовых возможностей предприятия (то есть характеристик производства «на входе»), но и особенностей получаемых отходов и побочных продуктов, уровня загрязнения окружающей среды с учетом действующего экологического законодательства и других факторов (то есть характеристик производства «на выходе»). В отдельных случаях весьма существенными оказываются ограничения по времени, например, если предприятие испытывает сложности с поставками сырья в определенные периоды в течение года.

Помимо задачи оптимизации выпуска, нельзя не упомянуть еще о двух типах задач, которые решаются с помощью метода линейного программирования: это так называемые транспортные задачи и задачи составления расписания.

Множеству предприятий и торговых организаций приходится ежедневно решать проблему, как наилучшим способом доставить товар потребителям, находящимся на разных расстояниях и в разных направлениях, да еще с учетом объема заказанной партии товара. Транспортная задача – это задача минимизации затрат на эксплуатацию транспортных средств при существующих ограничениях на имеющееся их количество, грузоподъемность, продолжительность рабочего дня при необходимости обслужить как можно большее количество заказов.

Задача составления расписания заключается в таком структурировании времени работы коллектива предприятия, которое было бы максимально удобно для всех его сотрудников и клиентов. Особенно актуальна эта проблема для предприятий сферы услуг, а также образовательных учреждений. Например, если известно, что максимальное количество покупателей приходит в магазин с 15 до 19 часов по будним дням и с 11 до 16 часов по субботам и воскресеньям, то и количество сотрудников, чьи рабочие часы приходятся на это время, должно соответствовать наплыву клиентов. График работы смен должен обеспечивать максимальную численность персонала в торговом зале именно в эти часы. Составление графика работы сотрудников на таких предприятиях можно считать задачей линейного программирования. Типичная постановка задачи линейного программирования в данном случае такова: максимизация количества обслуженных покупателей при имеющихся ограничениях, касающихся количества сотрудников, а также с учетом требований законодательства по поводу продолжительности рабочего дня и количества выходных дней в неделю для каждого сотрудника.

В рассмотренном нами примере целевая функция и ограничения линейные, и характер их не меняется со временем. Это далеко не всегда бывает так. Например, одним из факторов, определяющих целевую функцию и систему ограничений, может быть время. Такие задачи решают с помощью методов динамического программирования. Математическое программирование включает также методы нелинейного, стохастического, выпуклого программирования. Эти методы гораздо более сложны и, к сожалению, для решения практических задач применяются крайне редко.