5.Виведіть формулу дебіту газової св. В разі припливу ідеального газу за нелінійним законом.

Закон Дарсі під час фільтрації газу до свердловини в більшості випадків порушується, особливо за великих дебітів. У таких випадках фільтрацію звичайно описують двочленною формулою:

. (8.42)

Формули розподілу тиску і дебіту газової свердловини одержимо, безпосередньо інтегруючи рівняння (8.42).

Попередньо записуємо:

; . (8.43)

Тоді, підставляючи  і v у рівняння (8.42), маємо:

. (8.44)

Скорочуючи, розділяючи змінні й інтегруючи, знаходимо рівняння розподілу тиску, тобто:

; (8.45)

; (8.46)

; (8.47)

. (8.48)

Зіставляючи формули (8.30) і (8.48), доходимо висновку, що в разі порушення закону Дарсі лійка депресії тиску ще крутіша. Враховуючи велику кривину лійки депресії, ще раз переконуємося в справедливості припущення про ізотермічність процесу фільтрації газу, оскільки основна зміна температури внаслідок дросельного ефекту відбувається в найближчій околиці свердловини.

Оскільки для , то з рівняння (8.47) одержуємо формулу дебіту газової свердловини в разі припливу ідеального газу за двочленним законом:

(8.49)

або

, (8.50)

де коефіцієнти фільтраційного опору

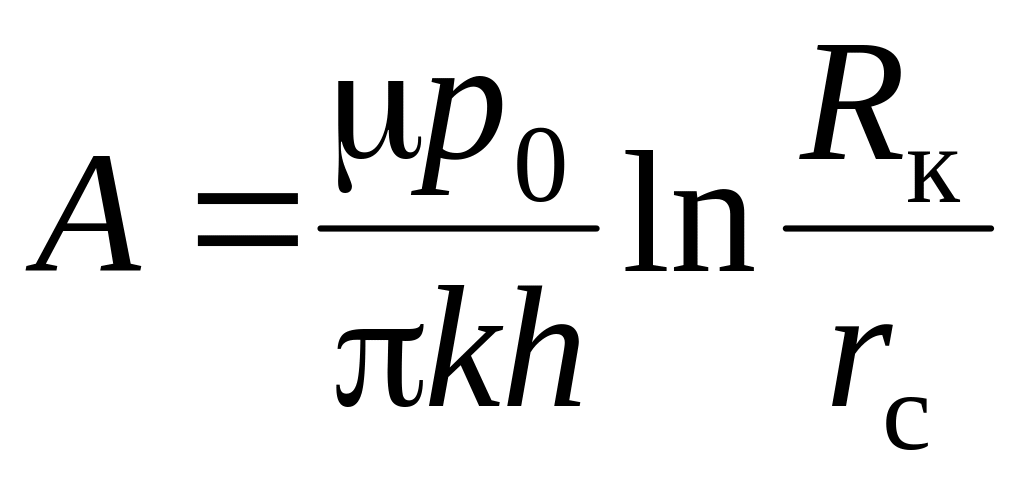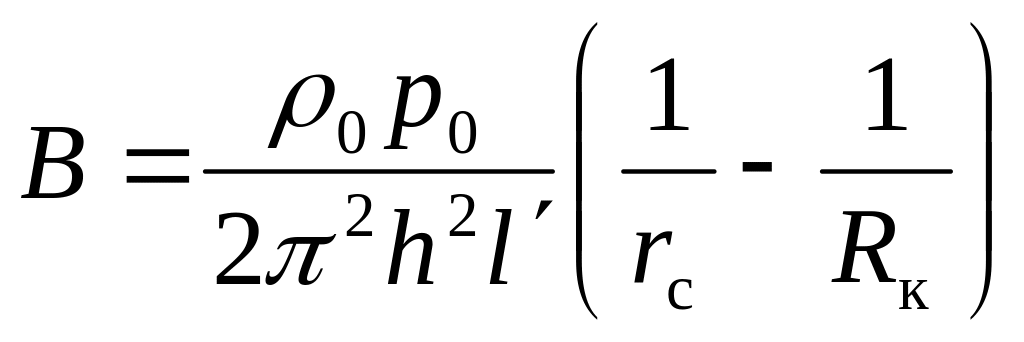; . (8.51)

6.У чому полягає суть методу суперпозиції?На чому базується можливість його застосування?Як визначити вектор дійсної швидкості руху частинки рідин в заданій точці пласта,коли працюють у ньому видобувні і нагнітальні св.

Метод суперпозиції (або накладання потоків) базується на принципі суперпозиції. Суть принципу суперпозиції полягає в тому, що для будь-якого лінійного диференціального рівняння можна одержати довільну кількість частинних розв’язків, алгебрична сума яких дає новий частинний розв’язок. Він виражає фізичний зміст незалежності ефектів, що викликані різними причинами, і застосовується в теоріях теплопровідності, електрики тощо. Звідси метод суперпозиції у підземній гідрогазомеханіці дає змогу одержати незалежні частинні (окремі) розв’язки лінійних диференціальних рівнянь для окремих (поодиноких) діянь (впливів) на фільтраційний потік, а загальний розв’язок у разі сумісної дії усіх впливів отримують підсумовуванням (додаванням) частинних розв’язків.

Математична суть методу суперпозиції полягає в такому. Якщо маємо кілька фільтраційних потоків з потенціалами , кожний з яких задовольняє лінійне рівняння Лапласа

, (6.10)

то і сума

(6.11)

також задовольняє рівняння Лапласа

, (6.12)

де – довільні постійні.

Гідродинамічна суть методу суперпозиції полягає в тому, що потенціал (тиск) у будь-якій точці пласта дорівнює алгебричній сумі потенціалів окремих стоків і джерел, а результуюча швидкість фільтрації – геометричній (векторній) сумі швидкостей фільтрації, викликаних роботою кожного стоку і джерела.

Останнє аналогічно випливає з лінійного рівняння нерозривності потоку (3.14) щодо вектора швидкості фільтрації.

Нехай на безмежній площині маємо n стоків і джерел (рис. 6.2). Потенціал кожного з них у точці M визначається за формулами (6.5) чи (6.6). Тоді за методом суперпозиції потенціалів у точці M у разі одночасної роботи цих стоків і джерел

(6.13)

aбо

, (6.14)

де – відстань від точки M до  -го стоку чи джерела; 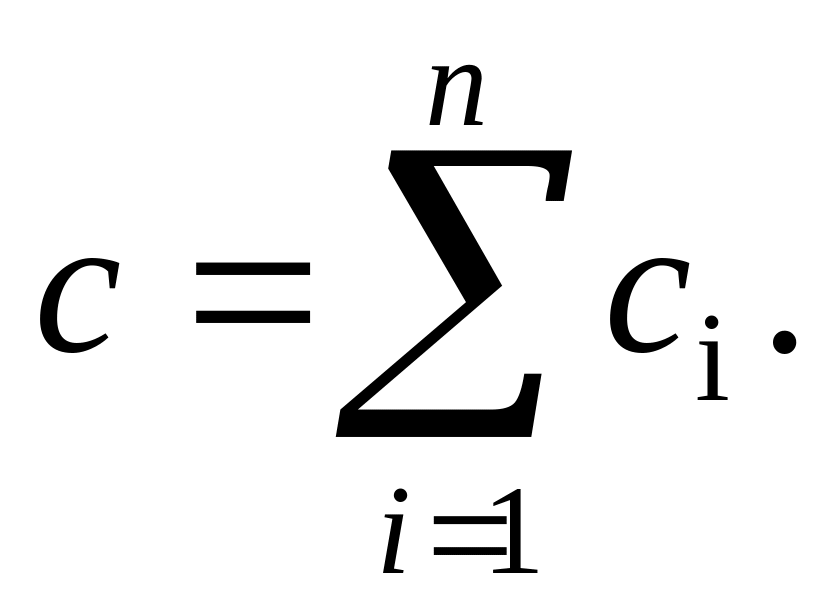Фізично це означає, що фільтраційні потоки від роботи кожного стоку та джерела накладаються один на один.

Вектор швидкості фільтрації у точці M

, (6.15)

де

У точці M можна знайти також вектор дійсної швидкості руху частинок:

, (6.16)

де т – коефіцієнт пористості пласта (скалярна величина).