1.Що таке коеф. Додаткового фільтраційного опору? Як його можна обчислити і визначити за рез. Дослідження св.?

Надходження рідини із пласта у стовбур недосконалої свердловини дещо утруднено, ніж у досконалу свердловину, оскільки площа фільтраційної поверхні недосконалої свердловини менша, виникає додатковий фільтраційний опір, тому і дебіт її менший.

Формулу Дюпюї для пояснення цього можна записати так:

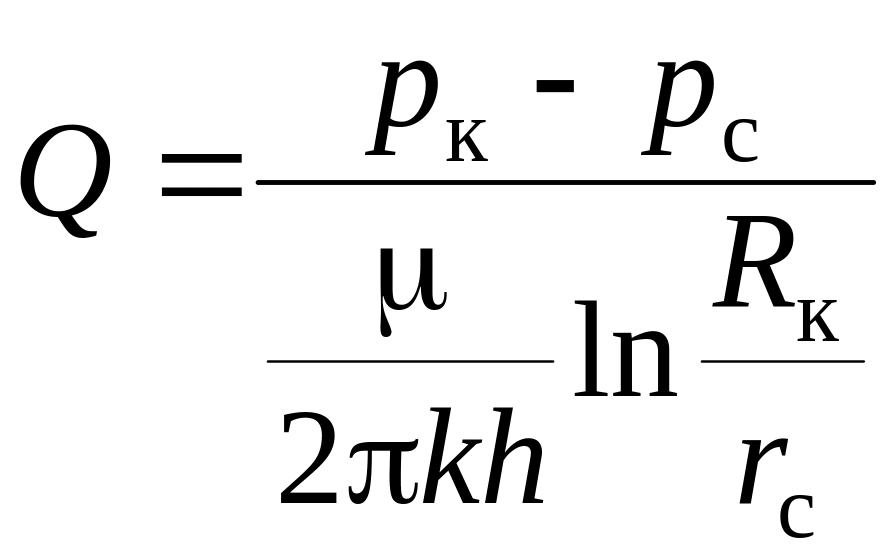. (7.4)

Тут легко побачити аналогію з формулою закону Ома, коли дебіт Q відповідає силі струму, різниця тисків – різниці напруг, а знаменник – електричному опору (принцип ЕГДА), тобто аналогію між усталеним рухом рідини в пористому середовищі і електричним струмом у суцільному провіднику (див. § 6.6). Тому знаменник формули (7.3) можна розглядати як фільтраційний опір потоку в пористому середовищі до досконалої свердловини. Очевидно, що із збільшенням знаменника (7.4) дебіт зменшуватиметься. Відносячи різницю в дебітах Q та Q_доск за рахунок різниці у фільтраційних опорах недосконалої та досконалої свердловин, формулу дебіту гідродинамічно недосконалої свердловини записуємо через коефіцієнт додаткового фільтраційного опору у вигляді:

, (7.5)

або

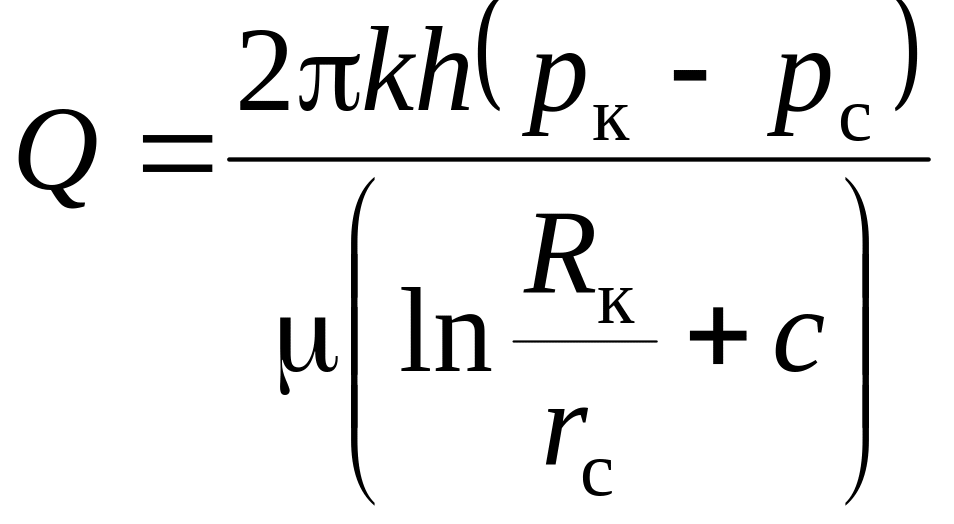, (7.6)

де – додатковий фільтраційний опір недосконалої свердловини; с – коефіцієнт додаткового фільтраційного опору.

2.На підставі чого і як можна поширити розвязки для усталеної фільтрації нестисливої рідини на усталену фільтрацію газу? Обгрунтуйте відповідь.

Раніше ми записали стосовно до усталеної фільтрації нестисливої рідини рівняння нерозривності потоку, руху (закону Дарсі) та фільтрації у вигляді (див. підрозд. 3.1, 3.2

; (8.1)

; (8.2)

. (8.3)

Для стисливих флюїдів (нафти, води, газу) густина ρ є функцією тиску p, тобто . Оскільки вздовж шляху фільтрації (лінії течії) тиск зменшується (рух відбувається в бік меншого тиску), то густина стисливого флюїду при цьому змінюється (точніше зменшується). Такі ж рівняння для стисливого флюїду ми записували у вигляді (див. підрозд. 3.1, 3.2, 3.5):

; (8.4)

; (8.5)

. (8.6)

Помноживши рівняння руху (8.2) і (8.5) на площу фільтрації як функцію довжини шляху фільтрації , дістанемо вирази закону Дарсі через витрати відповідно для нестисливого й стисливого флюїдів:

; (8.7)

, (8.8)

де – масова витрата стисливого флюїду (добуток масової швидкості фільтрації на площу фільтрації), причому відомо, що

. (8.9)

Зіставляючи відповідні рівняння для нестисливої рідини і стисливого флюїду, бачимо таку аналогію (відповідність):

Нестислива рідина		Стисливий флюїд
Швидкість фільтрації Тиск Об’ємна витрата	р Q	Масова швидкість фільтрації Функція Лейбензона Масова витрата	Р Qм

Отже, всі одержані раніше формули для усталеної фільтрації нестисливої рідини можна використати і для усталеної фільтрації стисливого флюїду (рідини чи газу), тільки в них за аналогією треба формально замінити v, p і Q на , Р і Q_м.