Основной закон фильтрации

Закономерности фильтрации жидкости в песчаных грунтах впервые исследовались французским инженером А. Дарси в 1852  1855 гг. Сущность опытов (рис. 1) сводилась к определению зависимости расхода воды Q в трубе, заполненной песком, от раз­ности гидродинамических напоров на концах трубы (H₁—H₂), дли­ны I и площади поперечного сечения ω трубы. Разность гидроди­намических напоров здесь представляет потери напора (h_w = H₁— H₂). Было установлено, что количество воды Q, фильтрующейся через песок в единицу времени (расход воды), прямо пропорцио­нально площади сечения ω, разности гидродинамических напоров h_w = H₁—H₂ и обратно пропорционально длине l пути фильтрации: (1)

где k — коэффициент пропорциональности, зависящий от физиче­ских свойств грунта, фильтрующейся жидкости и называемый ко­эффициентом фильтрации; I—пьезометрический уклон (I=h_/l)

.

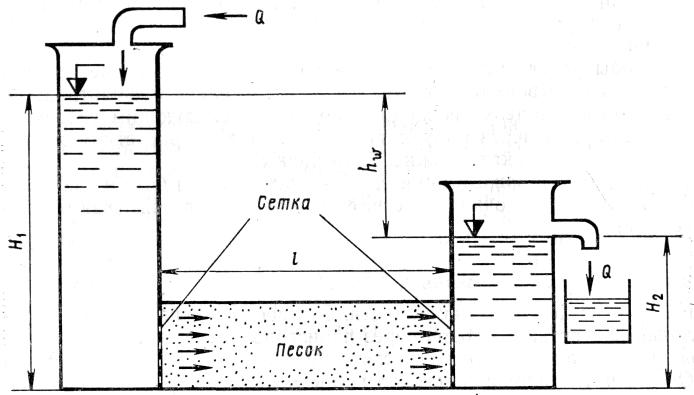
Рис. 1

Из (1) с учетом того, что q = uω, следует другая форма записи основного закона фильтрации: u=kI. (2)

Коэффициент фильтрации k численно равен скорости фильтра­ции при гидравлическом уклоне, равном единице, и имеет раз­мерность скорости.

Основной закон ламинарной фильтрации, или закон Дарси, в соответствии с выражениями (1), (2) можно сформулиро­вать так:

• расход Q фильтрующей жидкости пропорционален площади фильтрации ω и пьезометрическому уклону I;

• скорость фильтрации и пропорциональна коэффициенту фильт­рации k и пьезометрическому уклону I;

• удельные потери напора I при фильтрации пропорциональны скорости фильтрации и и обратно пропорциональны коэффициен­ту фильтрации k.

В дифференциальной форме линейный закон фильтрации име­ет вид: (3)

где и — местные скорости в точках потока; h — пьезометрические напоры в этих точках; ds — элементы длины. Величина dh/ds отрицательна, так как напор h по пути фильтрации уменьшается. Введение в формулу знака «минус» дает положительные значения скоростей.

О пределе применимости закона Дарси

Предел применимости линейного закона фильтрации Дарси в основном связан с границей ламинарного режима движения жид­кости в порах грунта. Академик H.H. Павловский впервые уста­новил критерий режимов движения жидкости в пористых средах и, как следствие, предел применимости линейного закона. Исход­ной для определения режима движения была формула числа Re, используемая при движении жидкости в трубах, Re = vd_тр/, где v — средняя скорость течения жидкости в трубопроводе, d_τρ — диаметр трубопровода,  — кинематический коэффициент вязкости. Академик H.H. Павловский получил выражение для числа Рейнольдса при фильтрации в виде: (4)

где т — коэффициент пористости; v — скорость фильтрации, см/с; d — эффективный диаметр частиц грунта, см;  — коэффициент ки­нематической вязкости, см²/с. H.H. Павловский установил крити­ческие значения числа Re _KР = 7,5  9. Линейный закон фильтраций остается в силе при Re < Re _KР.

Неудобство формулы (4) состоит в том, что в нее входит эффективный диаметр d, от определения значения которого суще­ственно зависит и число Re. Более поздние исследования В.H. Щелкачева, M.Д. Миллионщикова, Ф.И. Котяхова и др. позволили представить выражение для числа Re в виде:

(5)

где β— поправочный коэффициент, зависящий от формы и шеро­ховатости стенок поровых каналов, коэффициента пористости.

Из­вестна также формула В.H. Щелкачева: где все обозначения прежние. Критические значения числа Re, от­вечающие этой формуле, заключены в интервале Re _KР = 112.