5.2 Свободная конвекция жидкости в ограниченном объеме

Свободная конвекция наблюдается при охлаждении стали в стальковше в процессе его транспортировки между агрегатами внепечной обработки стали, между агрегатами и МНЛЗ, а также при разливке стали. Свободная конвекция имеет место также после разливки стали в изложницы в процессе затвердевания слитка, а также на участках жидкой фазы затвердевающих непрерывных слитков, находящихся ниже кристаллизатора на 2-3 м. Примеры свободной конвекции приведены на рис.5.4.

Рис.5.4. Примеры циркуляции металла при свободной конвекции: а) сталеразливочный ковш; б) затвердевающий слиток в изложнице; в) затвердевающая непрерывная заготовка. 1- шлак, 2 – контур циркуляции, 3 – жидкая фаза, 4- твердая корка, А-А – среднее сечение для выбора характерного перепада температуры в жидком металле, d – характреный размер объема

Уравнения Навье-Стокса выведены без учета зависимости физических параметров жидкости от температуры, в частности, не учтена зависимость плотности от температуры. Между тем свободное движение жидкости определяется разностью плотностей холодных и нагретых частиц жидкости. Учтем изменение плотности от температуры приближенно с помощью коэффициента объемного расширения β. Примем, что β не зависит от температуры в изучаемом диапазоне температур. Это условие лучше выполняется для газов и хуже для капельных жидкостей. Из определения β следует:

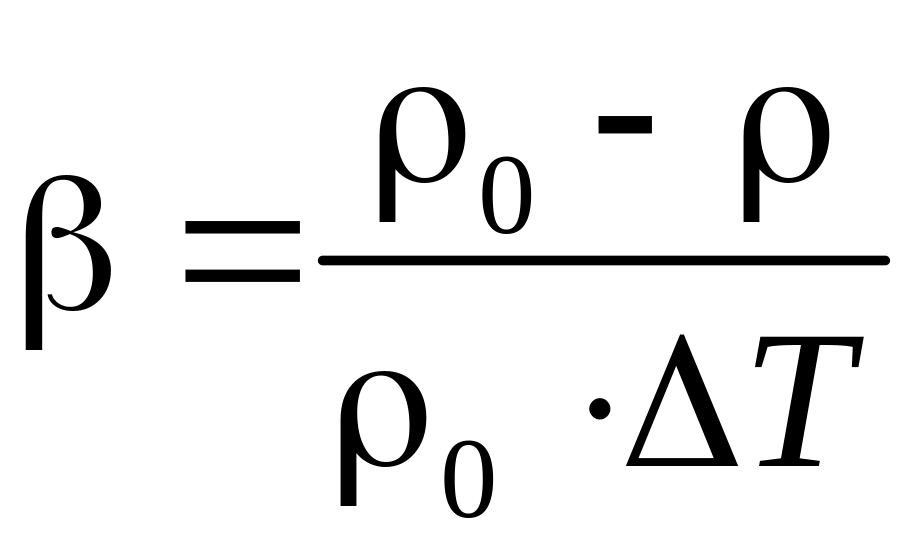, (5.5)

где ρ и ρ₀ – плотности, соответствующие температурам t и t₀, Δt= t-t₀.

Из последнего соотношения следует, что

. (5.6)

Подставляем ρ в уравнение (5.1), получаем уравнение движения жидкости при свободной конвекции:

.

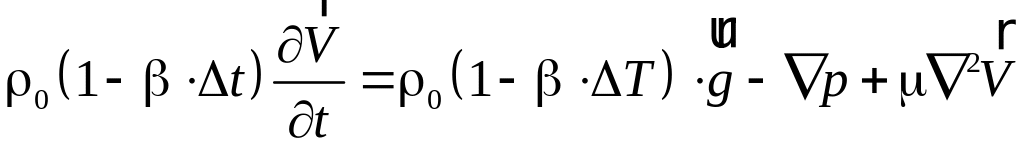Рассмотрим член . Этот член можно трактовать как алгебраическую сумму силы тяжести и подъемной силы . Для многих задач конвективного теплообмена с достаточным приближением можно ограничиться только учетом подъемных сил (здесь ρ является фиксированным значением плотности). Учитывая, что 1>>βΔt, пренебрежем переменностью ρ. В результате получим уравнение движения жидкости при свободной конвекции в векторной форме записи:

, (5.7)

где , - коэффициент динамической вязкости.

Модель процесса тепломассопереноса при свободной конвекции включает уравнение (5.7), уравнение теплопереноса и уравнение неразрывности. Как уже отмечалось в п. 4.1. решение подобной задачи встречает определенные трудности. Поэтому, в случаях, когда интересует только общее влияние свободной конвекции на теплоперенос, то ее учитывают также путем введения вместо коэффициента теплопроводности коэффициента эффективной теплопроводности по формуле [27]:

, (5.8)

где - критерий Грасгофа, который характеризует соотношение подъемной силы, возникающей вследствие разности плотностей в жидкости, к силе вязкости; d – характерный размер ограниченного объема, Pr=ν/a - критерий Прандтля, характеризующий подобие полей скорости и температуры.

Характерная величина d соответствует наименьшему размеру контура циркуляции жидкости при свободной конвекции (рис. 5.4). Перепад температур равен разности максимального и минимального значений температуры в сечении А-А на рис. 5.4 Максимальная температура, как правило, наблюдается на оси ковша или слитка, минимальная – в месте контакта или на границе твердой и жидкой фаз (фронте кристаллизации металла) при затвердевании слитка. Среднее сечение А-А выбирается перпендикулярно направлению подъемных сил.

В общем случае при наличии вынужденной и свободной конвекции коэффициент эффективной теплопроводности определяют по формуле:

(5.9).