Лекция 13. Цилиндрические зубчатые передачи.

Геометрия и кинематика эвольвентного зацепления. Зубчатые передачи в преобладающем большинстве изготавливают с эвольвентным профилем зубьев. Это объясняется тем, что эвольвентное зацепление имеет ряд существенных достоинств: простое изготовление и постоянство передаточного отношения, малые скорости скольжения и долговечность колес.

Э вольвентой (рис.6.2) называют кривую, описываемую точкой С прямой АВ, перекатывающейся без скольжения по окружности диаметра d_b, которую называют основной окружностью.

Для таких передач общая нормаль NN к взаимодействующим профилям (рис.6.3), в любой момент движения сопряженных зубьев должна проходить через точку П – полюс зацепления, лежащий на линии центров и делящий межосевое расстояние на отрезки, обратно пропорциональные передаточному отношению 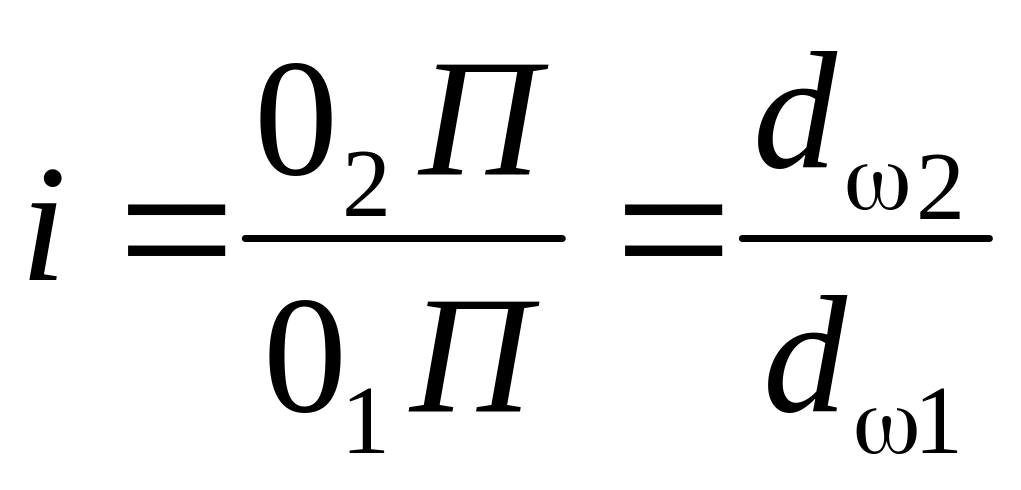, где d_ω2 и d_ω1 – диаметры воображаемых окружностей, касающихся друг друга в полюсе зацепления П и перекатывающихся при вращении одна по другой без скольжения. Эти окружности называются начальными окружностями. Прямая NN называется линией зацепления, т.к. она является траекторией точек контакта сопряженных зубьев при вращении колес. Угол α_ω между линией зацепления и прямой, перпендикулярной межосевой линии О₁О₂ называется углом зацепления.

В ершины и впадины зубьев очерчиваются соответственно окружностями выступов с диаметрами , и впадин – , .

В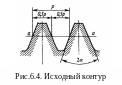 качестве исходного контура для эвольвентного зацепления принят контур, расположенный на прямой – рейка (рис.6.4). Линия а-а, на которой толщина зуба равна ширине впадины, называется средней линией рейки.

Расстояние р между соответственными точками профилей соседних зубьев, измеренное вдоль средней линии, называется шагом зацепления , а отношение – модулем зацепления.

Применительно к зубчатому колесу окружность, на которой шаг равен шагу исходного контура р, называется делительной окружностью d. Очевидно, что , где z – число зубьев колеса. Откуда . Соответственно, окружной модуль представляет собой частное от деления диаметра делительной окружности на число зубьев колеса. Часть зуба, расположенная между окружностями выступов и делительной, называется головкой зуба h_a, а между окружностью впадин и делительной – ножкой зуба h_f.

Цилиндр, диаметр которого равен диаметру делительной окружности, называется делительным цилиндром. Кратчайшее расстояние по делительному цилиндру между одноименными профильными поверхностями двух смежных зубьев называется нормальным шагом р_n (рис.6.5). Справедлива зависимость , где  – угол наклона линии зуба. Нормальный модуль вычисляется по формуле . Для прямозубых передач ( = 0) окружные и нормальные шаги и модули соответственно совпадают. Величины модулей определяются стандартом. Для косозубых цилиндрических колес стандартными являются нормальные модули.

Для цилиндрических зубчатых передач должны выполняться следующие соотношения:

- межосевое расстояние

- высота головки зуба h_a = m;

- высота ножки зуба h_f = 1,25m;

- высота зуба h = h_a + h_f = 2,25m;

- диаметры делительные (начальные) , ;

- диаметры вершин зубьев , ;

- диаметры впадин зубчатых колес , ;

- угол зацепления ;

передаточное число зубчатой передачи равно отношению числа зубьев колеса к числу зубьев шестерни u = z₂ / z₁.

О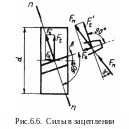 тношение активной части линии зацепления АВ к шагу р_t называется коэффициентом перекрытия зубьев . Он показывает, сколько пар зубьев одновременно находятся в работе. Коэффициент перекрытия в большой степени определяет плавность работы передачи. Для прямозубых передач он должен быть больше 1.

Силы, действующие в цилиндрических передачах (рис.6.6). Нормальную силу F_n , давления одного зуба на другой, возникающую при работе сопряженных зубьев можно разложить на и , а , в свою очередь, на и .

В результате имеем

,

где F_t – окружная сила, , Т – вращающий момент, d – делительный диаметр.

Из схемы сил

, ,

где F_r – радиальная, а F_a – осевая силы, – угол зацепления, – угол наклона линии зуба.

Нормальная к поверхности зуба сила .

Расчет зубьев цилиндрических передач и расчет на контактную прочность в большинстве случаев является основой для определения габаритных размеров передачи. Исходной зависимостью для расчета контактных напряжений (рис.6.7), возникающих на рабочих поверхностях зубьев служит формула Герца-Беляева

,

где Z_Е – коэффициент, учитывающий механические свойства контактирующих материалов; q – нормальная нагрузка на единицу длины контактной линии; – приведенный радиус кривизны контактирующих поверхностей, R₁ и R₂ – радиусы кривизны профилей контактирующих зубьев.

Подставляя в эту формулу параметры и характеристики цилиндрических зубчатых передач с эвольвентным профилем зубьев, после ряда преобразований получим формулу для расчета контактной прочности рабочих поверхностей зубьев

,

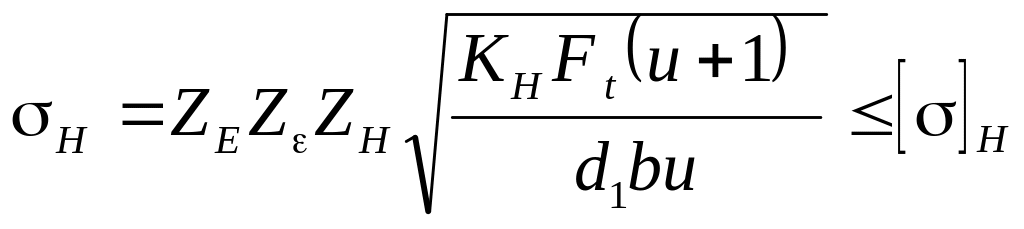где Z_Е – коэффициент, учитывающий механические свойства материалов шестерни и колеса; Z_ – коэффициент, учитывающий суммарную длину контактных линий; Z_Н – коэффициент, учитывающий форму сопряженных поверхностей зубьев; К_Н – коэффициент нагрузки (учитывает динамическую нагрузку и неравномерность распределения нагрузки по ширине зуба и между зубьями); F_t – окружная сила на делительном диаметре d₁; b – ширина венца колеса; u – передаточное число.

Формулу для проектного расчета, определяющую приближенно межосевое расстояние a_w получают из последнего условия, используя выражения ; ; и подставив вместо коэффициентов , и их значения:

,

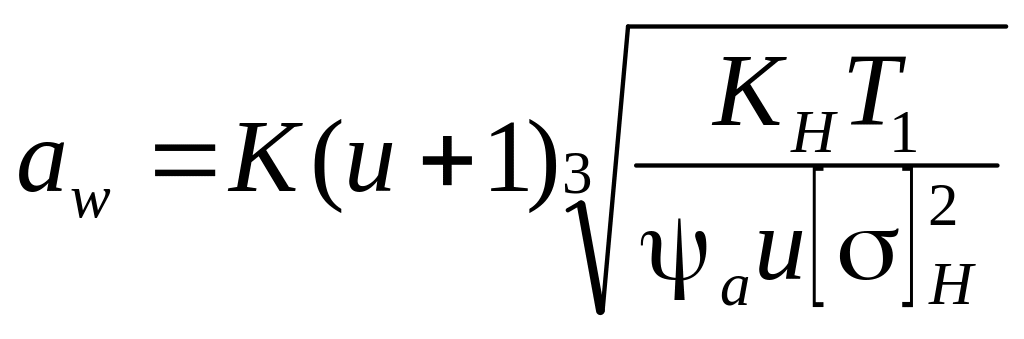где К – коэффициент, учитывающий свойства и геометрию колес – для прямозубых передач К = 450, для косозубых – К = 410; _а = b/a_w – коэффициент ширины колеса принимается по стандартному ряду в зависимости от расположения колес относительно опор; Т₁ – крутящий момент на шестерне.

Расчет зубьев на изгиб выполняют для определения основного параметра зубьев – модуля зацепления m, а также для проверки прочности зубьев на излом. Максимальные напряжения изгиба возникают у основания зуба, в тот момент, когда сила приложена к его вершине и передается одной парой зубьев (рис.6.8). Зуб будем рассматривать как консольную балку, нагруженную в вершине нормальной силой F_n, которую разложим на две составляющие:

; .

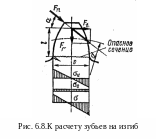
Напряжения изгиба и сжатия в основании зуба

; ,

где – момент сопротивления при изгибе; – площадь сечения основания зуба. Выражая плечо l₁ и размер s через модуль: ; (μ и γ – коэффициенты пропорциональности), получим результирующее напряжение

;

где – коэффициент формы зуба; – теоретический коэффициент по концентрации напряжений.

Введя поправочные коэффициенты, получим формулу для расчета изгибной прочности зубьев

,

где b – ширина колеса; m – нормальный модуль; ; – коэффициенты, учитывающие динамическую нагрузку, неравномерность распределения нагрузки по ширине зуба и между зубьями; – коэффициент, учитывающий форму зубьев (определяется по таблице); и – коэффициенты, учитывающие соответственно перекрытие зубьев и угол наклона зуба.

Если прочность на изгиб является основным критерием работоспособности (для зубчатых колес высокой твердости), полученную формулу решают относительно модуля с учетом соотношений ; ; .