Pressure integration [edit]

The force on the wing can be examined in terms of the pressure differences above and below the wing, which can be related to velocity changes by Bernoulli's principle.

The total lift force is the integral of vertical pressure forces over the entire wetted surface area of the wing:^[93]

where:

• L is the lift,

• A is the wing surface area

• p is the value of the pressure,

• n is the normal unit vector pointing into the wing, and

• k is the vertical unit vector, normal to the freestream direction.

The above lift equation neglects the skin friction forces, which typically have a negligible contribution to the lift compared to the pressure forces. By using the streamwise vector i parallel to the freestream in place of k in the integral, we obtain an expression for the pressure drag D_p (which includes induced drag in a 3D wing). If we use the spanwise vector j, we obtain the side force Y.

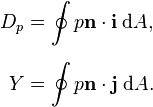
One method for calculating the pressure is Bernoulli's equation, which is the mathematical expression of Bernoulli's principle. This method ignores the effects of viscosity, which can be important in the boundary layer and to predict friction drag, which is the other component of the total drag in addition to D_p.

The Bernoulli principle states that the sum total of energy within a parcel of fluid remains constant as long as no energy is added or removed. It is a statement of the principle of the conservation of energy applied to flowing fluids.

A substantial simplification proposes that other forms of energy changes are inconsequential during the flow of air around a wing and that energy transfer in/out of the air is not significant, so the sum of pressure energy and speed energy for any particular parcel of air must be constant. Consequently, an increase in speed must be accompanied by a decrease in pressure and vice-versa. It is named for the Dutch-Swiss mathematician and scientist Daniel Bernoulli, though it was previously understood by Leonhard Euler and others.

Bernoulli's principle provides an explanation of pressure difference in the absence of air density and temperature variation (a common approximation for low-speed aircraft). If the air density and temperature are the same above and below a wing, a naive application of the ideal gas law requires that the pressure also be the same. Bernoulli's principle, by including air velocity, explains this pressure difference. The principle does not, however, specify the air velocity. This must come from another source, e.g., experimental data.

In order to solve for the velocity of inviscid flow around a wing, the Kutta condition must be applied to simulate the effects of viscosity. The Kutta condition allows for the correct choice among an infinite number of flow solutions that otherwise obey the laws of conservation of mass and conservation of momentum.

20. Write the formula of experimental aerodynamics for drag force, to term values, which are contained in this formula.

where

F_D is the drag force, which is by definition the force component in the direction of the flow velocity,^[1]

ρ is the mass density of the fluid, ^[2]

v is the velocity of the object relative to the fluid,

A is the reference area, and

C_D is the drag coefficient – a dimensionless coefficient related to the object's geometry and taking into account both skin friction and form drag.

The equation is attributed to Lord Rayleigh, who originally used L² in place of A (with L being some linear dimension).^[3]