Построение имитационной модели
В данной системе транзакты генерируются согласно распределению Пуассона. Время обслуживания транзактов в каналах распределено согласно экспоненциальному закону распределения.
При имитационном моделировании данной системы массового обслуживания для создания генератора случайных чисел распределения Пуассона использовался метод связи с биноминальным распределением.
Биномиальное
распределение в теории вероятностей –
распределение количества «успехов» в
последовательности из
независимых случайных экспериментов,
таких что вероятность «успеха» в каждом
из них равна
.
Пусть
– конечная последовательность независимых
случайных величин с распределением
.
Построим случайную
величину
:
Тогда
-
число единиц (успехов) в последовательности
,
имеет биноминальное распределение с
степенями свободы и вероятностью
«успеха»
.
Это записывается как
.
Если
большое, а
– фиксированное число, то
,
где
– распределение Пуассона с параметром
.
Экспоненциальное
распределение может быть получено из
непрерывного равномерного распределения
методом обратного преобразования. Пусть
,
тогда
Алгоритм работы программы следующий:
Генератор случайных чисел выдает транзакты согласно распределению по закону Пуассона. Далее по экспоненциальному закону распределения происходит присвоение поступившему транзакту времени его обслуживания.
Далее происходит проверка на принадлежность обслуживания требования в одной из касс и постановка его в очередь, что, в свою очередь, дает возможность рассчитывать требуемые параметры.
Программа моделирования реализована в интегрированной среде разработки Microsoft Visual Studio 2008 в виде консольного приложения, текст которой приведен в приложении.
Результат работы программы представлен на рис. 1.
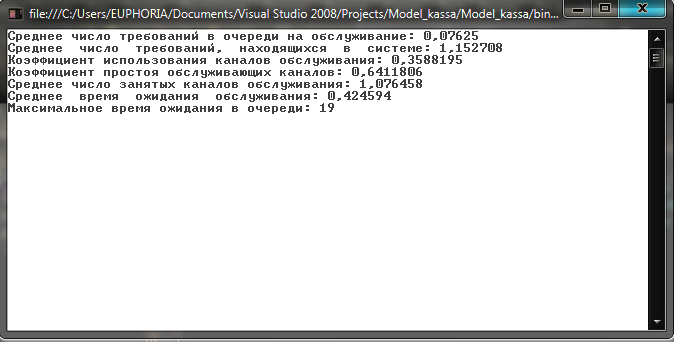
Рис. 1. Результаты работы имитационной модели
Заключение
В результате выполнения контрольно-курсовой работы было рассмотрено имитационное моделирование, которое является распространенным методом исследования на всех этапах создания и функционирования сложной системы. В результате была создана программа, моделирующая работу многоканальной системы массового обслуживания с ожиданием. Также были определены основные характеристики данной системы.
Список литературы
1. Пасько, Николай Иванович. Статистическое моделирование процессов и систем: учеб. пособие для вузов / Н.И. Пасько, А.Н. Иноземцев, С.Г. Зайков; ТулГУ .— Тула: Изд-во ТулГУ, 2008 .— 112 с.
2. Советов, Б.Я. Моделирование систем: учебник для вузов / Б.Я. Советов, С.А. Яковлев.— 4-е изд., стер. — М.: Высш. шк., 2005.— 342 с.
Приложение Листинг файла Programm.Cs
using System;
using System.Collections.Generic;
using System.Text;
namespace Model_kassa
{
class Program
{
static void Main(string[] args)
{
bool
isBusy1 = false,
isBusy2 = false,
isBusy3 = false;
int
time1 = 0, //время обработки заявки на 1 кассе
time2 = 0,
time3 = 0;
int avrQueue = 0; //сумма(заявок в очереди в каждый момент времени)
int avrWork = 0;
int avrTimeQueue = 0; //время пребывания в очереди вcех заявок
int timeQueueN = 0; //сколько этих заявок
int maxTime = 0; //макс. время в очереди
List<int> queue = new List<int>();
for (int i = 0; i < 80; i++)
{
int N = RandPuas();
N = 60 / N;
for (int n = 0; n < 60; n++)
{
if (n % N == 0)
queue.Add(0);
if (!isBusy1)
{
if (queue.Count > 0)
{
time1 = RandEx();
isBusy1 = true;
avrTimeQueue += queue[0];
timeQueueN++;
if (queue[0] > maxTime)
maxTime = queue[0];
queue.RemoveAt(0);
}
}
else
{
avrWork++;
time1--;
if (time1 <= 0)
{
isBusy1 = false;
}
}
if (!isBusy2)
{
if (queue.Count > 0)
{
time2 = RandEx();
isBusy2 = true;
avrTimeQueue += queue[0];
timeQueueN++;
if (queue[0] > maxTime)
maxTime = queue[0];
queue.RemoveAt(0);
}
}
else
{
avrWork++;
time2--;
if (time2 <= 0)
{
isBusy2 = false;
}
}
if (!isBusy3)
{
if (queue.Count > 0)
{
time3 = RandEx();
isBusy3 = true;
avrTimeQueue += queue[0];
timeQueueN++;
if (queue[0] > maxTime)
maxTime = queue[0];
queue.RemoveAt(0);
}
}
else
{
avrWork++;
time3--;
if (time3 <= 0)
{
isBusy3 = false;
}
}
avrQueue += queue.Count;//+=заявок в очереди в каждый момент времени
for (int p = 0; p < queue.Count; p++)
{
queue[p]++;
}
}
}
int avrN = 80 * 60;
Console.WriteLine("Cреднее число требований в очереди на обслуживание: {0}", (float)avrQueue / avrN);
Console.WriteLine("Cреднее число требований, находящихся в системе: {0}", (float)avrQueue / avrN + (float)avrWork / avrN);
Console.WriteLine("Коэффициент использования каналов обслуживания: {0}", ((float)avrWork / avrN) / 3);
Console.WriteLine("Коэффициент простоя обслуживающих каналов: {0}", 1 - ((float)avrWork / avrN) / 3);
Console.WriteLine("Среднее число занятых каналов обслуживания: {0}", (float)avrWork / avrN);
Console.WriteLine("Среднее время ожидания обслуживания: {0}", (float)avrTimeQueue / timeQueueN);
Console.WriteLine("Максимальное время ожидания в очереди: {0}", maxTime);
Console.Read();
}
static int RandPuas()
{
int ave = 10, s = 0;
for (int i = 0; i < 1000; i++)
{
if ((1000 * _rnd.NextDouble()) < ave)
s++;
}
return s;
}
static int RandEx()
{
double lambda = 0.16667;
double ri = _rnd.NextDouble();
return (int)((-1.0 / lambda) * Math.Log(1.0 - ri, Math.E));
}
static Random _rnd = new Random();
}
}