Электрохимия

Пример 1. По данным о стандартных электродных потенциалах меди и цин­ка рассчитайте ЭДС элемента, составленного из полуэлементов:

Значения стандартных электродных потенциалов находим в справочнике, так как медный полуэлемент более электроположителен, то

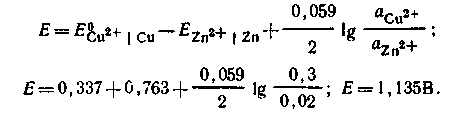
Пример 2. Рассчитайте ЭДС и напишите схему гальванического элемента, в котором обратимо протекает реакция по уравнению:

Решение. Определим уравнения электродных реакций. Для этого из уравнения реакции, приведенной в условии, вычитаем урав­нение одной из предполагаемых электродных реакций

В справочнике находим соответствующие стандартные электрод­ные потенциалы. Вычисляем электродные потенциалы по уравнению:

Подставляя значения Е₁ и Е₂ в уравнение:

Е = Е₁ – Е₂, получаем Е = 0,789 – 0,451 = 0,338 В. Схема элемента:

Пример 3. Рассчитайте константу равновесия реакции Cd²⁺ + Zn = Zn²⁺ + Cd, если Е⁰ (Сd²⁺/Cd) = -0,403 В; E⁰ (Zn²⁺/Zn) = -0,763 В.

Решение. Константу равновесия вычислим по уравнению:

при 298 К

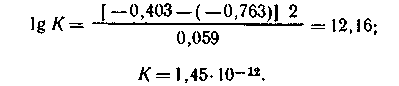
Пример 4. Вычислите полезную работу W реакции Ag + ½ Cl₂ = AgCl, используя стандартные электродные потенциалы, если p (Cl₂) = 1 атм, Т = 298 К.

Решение. Полезная работа реакции при p и Т = const бу­дет W = -ΔG. Для электрохимической реакции в стандартных ус­ловиях ΔG⁰ = -nE°F. ЭДС элемента равна Е° = E°₁ – E⁰₂, где E°₁ и E⁰₂ - стандартные потенциалы электродов, составляющих элемент. Рассматриваемая реакция осуществляется в элементе по схеме:

Адсорбция

Пример 1. Определить суммарную поверхность частиц, если при дроблении 1 г серы получили частицы: 1) кубической формы с длиной ребра, равной 10^-5 см; 2) частицы шарообразной формы с поперечником 2·10^-6 см. Плотность серы 2,07 г/см³.

Решение. 1. Используем формулу:

1 г серы занимает объем

Учитывая объем 1 г серы, получим суммарную поверхность частиц

2. Для частиц шарообразной формы используем формулу:

Учитывая объем серы, находим общую поверхность всех частиц:

Пример 2. Определить число частиц, образующихся при раздробленности 0,2 см³ ртути на правильные кубики с длиной ребра 8·10^-8 см. Плотность ртути равна 13,546 г/см³.

Решение. Находим массу 0,2 см³ ртути:

Определяем объем одной частицы:

Масса одной частицы будет равна:

Число частиц:

Пример 3. Определить поверхностный избыток (кмоль/м²) при 10 °С для раствора, содержащего 50 мг/л пеларгоновой кислоты С₈Н₁₇СООН. Поверхностное натяжение воды при данной температуре 74,22·10^-3 н/м, а исследуемого раствора 57,0·10^-3 н/м.

Решение. Определяем концентра­цию кислоты в кмоль/м³. В 1 л содержится 0,05 г кислоты. В 1 м³ этого раствора будет 0,05 кг кислоты, т.е. 0,05/158 кмоль/м³, где 158 – молярная масса пеларгоновой кислоты с₁ = 0.

Гак как Г > 0 и σ₂ < σ₁, то адсорбция положительна.

Пример 4. К 100 см³ раствора уксусной кислоты различной кон­центрации при 20 °С добавили по 3 г активированного угля. Количе­ство кислоты до и после адсорбции определяли титрованием 50 см³ раствора 0,1 н. раствором NaOH в присутствии фенолфталеина. Оп­ределить соотношение х/m для каждого раствора кислоты, используя данные титрования

Решение. Определяем нормальность N, титр Т и содержание уксусной кислоты (г) в 100 см³ раствора (с) до и после адсорбции.

До адсорбции:

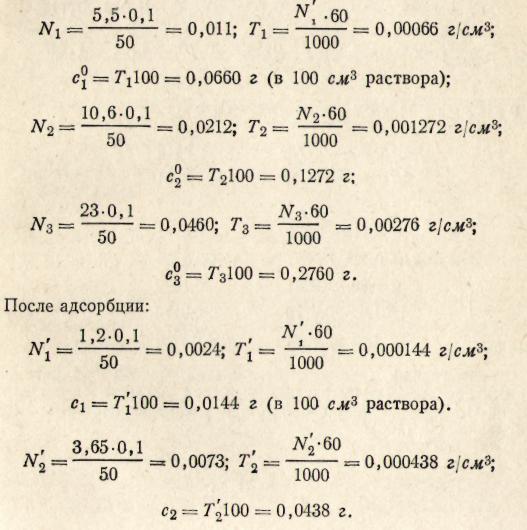
Определяем количество кислоты, адсорбировавшееся 1 г активированного угля,

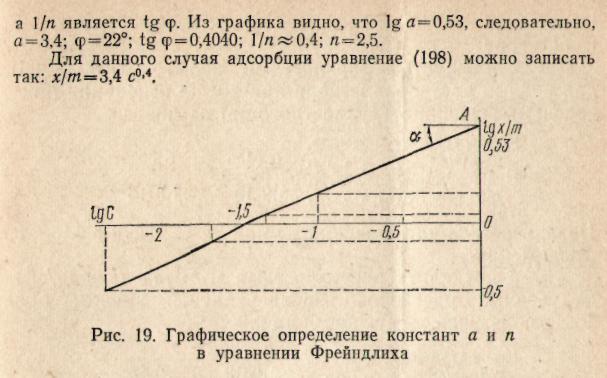
Пример 5. На основе опытных данных, полученных при изучении адсорбции углем бензойной кислоты из раствора ее в бензоле при 25 °С, определить графически константы а и 1/n в уравнении Фрейндлиха:

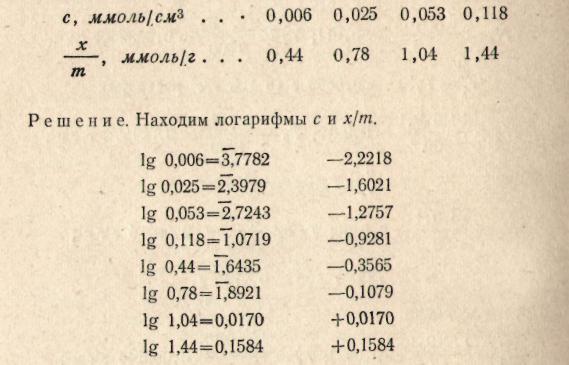
Строим график, откладывая на оси ординат lg х/m, а на оси абсцисс lg c. (Округляем значения логарифмов до сотых)

Отрезок ОА представляет собой lg а в уравнении изотермы адсорбции Фрейндлиха:

Пример 6. При адсорбции аргона коксовым углем при 194,7 К получены следующие результаты

Рассчитайте постоянные в уравнении Лэнгмюра.

Решение. Согласно уравнению Лэнгмюра а/а_∞ является уг­ловым коэффициентом прямой зависимости между Р/а и Р, а 1/bа_х – отрезком, отсекаемым этой прямой на оси ординат. Вычисляем величи­ны Р/а:

По полученным данным строим график, отложив на оси абсцисс Р, а на оси ординат – P/a. Как видно из графика (рис. 40):

Пример 7. Объем газообразного азота V_m при 1,04·10⁵ Па (750 мм рт. ст.) и 273 К, необходимый для покрытия образца силикагеля мономоле­кулярным слоем, 129 мл/г. Вычислите площадь поверхности 1 г силикагеля, если молекула азота занимает площадь 16,2·10^-20 м².

Решение. Площадь вычисляем по уравнению:

Пример 8. Превращение пероксида бензоила в диэтиловый эфир (реакция первого порядка) при 333 К прошло за 10 мин на 75,2 %. Вычислите константу скорости реакции.

Решение. Напишем уравнение первого порядка и подставим в него соответствующие значения:

Пример 9. Тростниковый сахар (биоза) в присутствии ионов Н⁺ гидролизуется водой, распадаясь на две монозы (глюкозу и фруктозу) по уравнению:

Раствор тростникового сахара вращает плоскость поляризации света вправо, а смесь глюкозы и фруктозы – влево. Угол вращения в обоих случаях пропорционален концентрации растворенных веществ. При 298 К в 0,5 н. растворе НCl при большом избытке воды изменение угла вращения α плоскости поляризации раствора тростникового сахара во времени t было следующее

Рассчитайте константу скорости реакции и количество сахара (%), которое инвертируется в течение 236 мин. Определите угол вращения к моменту времени t = 236 мин.

Решение. Обозначим угол вращения в начальный момент α₀, после окончания инверсии α_∞ и наблюдаемый в данный момент α₁. Так как от начального до конечного момента угол вращения изменит­ся на α₀ – α₁, то эта величина пропорциональна начальной концен­трации сахара с₀,_A, концентрация же сахара в данный момент с₀,_A – х пропорциональна изменению угла вращения от данного момента α₁ до конца инверсии α_∞, т.е. пропорциональна α_t – α_∞. Реакция инверсии сахара в присутствии большого избытка воды идет по первому порядку. Рассчитываем константу скорости реакции по уравнению, заменив с₀,_A и с₀,_A – х пропорциональными величинами α₀ – α_∞ и α_t – α_∞:

Определяем количество сахара, которое инвертируется в течение 236 мин. Для этого, подставив в уравнение вместо k₁ и t со­ответственно 0,005028 и 236 мин, получим

Откуда получаем количество гидролизованного сахара:

Определяем угол вращения, соответствующий t = 236 мин. Когда все начальное количество сахара проинвертирует, изменение угла вращения составит 25,16° - (-8,38°) = 33,54°. Так как при t = 236 мин остается 30,52 % сахара, не подвергшегося гидролизу, то изменение угла вращения, вызванное превращением этого количе­ства, будет соответственно меньше. Обозначим его через z, тогда

Так как z = α_t – (8,38°), то α_t = z – 8,38° = 10,23° - 8,38° = +1,85°, т.е. реагирующая смесь спустя 236 мин после начала ре­акции будет иметь правое вращение, равное 1,85°.

Пример 10. Скорость реакции (C₂H₅)₃N + CH₃I = [(C₂H₅)₃CH₃N]I в нит­робензоле определялась при 298 К, причем получены следующие дан­ные:

где t – время; х – количество триэтиламина и метилиодида, проре­агировавших за время t. Начальные концентрации амина и иодистого алкила равны 0,0198 моль/л. Рассматриваемая реакция – второго по­рядка. Определите константу скорости.

Решение. Для реакции второго порядка, в которой реагируют два вещества с одинаковыми концентрациями:

k = 0,0334; 0,0327; 0,0329; 0,0332; 0,0328; 0,0325.

Среднее значение k = 0,0329 л·моль^-1·с^-1.

Пример 11. Для химической реакции А = В константа скорости k = 0,5, исходная концентрация c_0,A = 1 моль/л. Вычислите степень превра­щения вещества А за время t = 1 ч, если реакция идет по нулевому, первому, второму порядку. Как зависит степень превращения от по­рядка реакции?

Решение. Для реакции, протекающей по нулевому порядку, согласно уравнению

Для реакции, протекающей по первому порядку, согласно уравнению

Для реакции, протекающей по второму порядку, согласно урав­нению

Чем выше порядок, тем меньше степень превращения, тем медленнее идет реакция.