Растворы

Пример 1. Вычислить число степеней свободы, которыми обла­дает система, состоящая из: а) раствора КNO₃ и NaNO₃ в присутст­вии кристаллов обеих солей и паров воды; б) раствора обеих солей в присутствии льда, кристаллов КNO₃, NaNO₃ и паров воды; в) рас­твора обеих солей в присутствии льда и паров воды.

Решение. Поскольку между КNO₃, NaNO₃ и водой не наблю­дается химического взаимодействия, то число компонентов равно числу составных частей системы, т.е. К = 3. Используем уравнение правила фаз для каждого случая (а), (б), (в): а) в равновесии находятся четыре фазы: жидкая, пары воды и две твердые (КNO₃ и NaNO₃). Следовательно, с = 3 + 2 – 4 = 1. Это одновариантная система.

б) число фаз, находящихся в равновесии, равно 5 (ф = 5): пары воды, жидкость, лёд, кристаллы КNO₃ и NaNO₃: с = 3 + 2 – 5 = 0. Безвариантная система. Степени свободы отсутствуют. Равнове­сие существует при строго заданных температуре и концентрациях солей.

в) число фаз, находящихся в равновесии, равно трём (ф = 3): па­ры воды, лёд, жидкий раствор двух солей: с = 3 + 2 – 3 = 2. Это двухвариантная система. Можно произвольно (до некоторого предела) изменять температуру и концентрацию одной из солей.

Пример 2. При сплавлении солей КСl и NaNO₃ возможна реакция

КСl + NaNO₃ = КNO₃ + NaСl

Определить число степеней свободы, если жидкий расплав нахо­дится в равновесии с кристаллами NaNO₃.

Решение. Число независимых компонентов находим по разности: число составных частей системы минус число химических реак­ций, протекающих в данной системе при данных условиях: к = 4 – 1 = 3; ф = 2 (жидкий расплав и кристаллы NaNO₃). Соли КСl, KNO₃, NaCl и NaNO₃ нелетучи. Поэтому можно счи­тать систему конденсированной. Используем уравнение правила фаз: с = к+1 – ф = 3 + 1 – 2 = 2. Система двухвариантна.

Пример 3. Температура кипения ртути под нормальным атмосфер­ным давлением 357 °С. Теплота парообразования 283,2 Дж/г. Опреде­лить изменение упругости пара ртути при изменении температуры на 1 ° вблизи температуры кипения ртути под нормальным атмосферным давлением

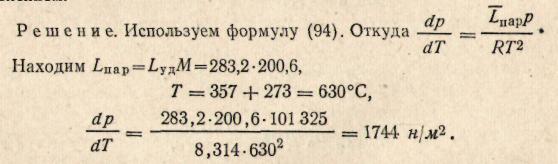
Пример 4. Давление паров воды при 97 ⁰С равно 90919,9 н/м², а при 103 ⁰С 112651,8 н/м². Определить давление паров воды при 110 ⁰С.

Пример 5. Удельная теплота плавления нафталина при его нор­мальной температуре плавления 79,9 °С равна 149,25 Дж/г. Разность удельных объемов в жидком и твердом состояниях при температуре плавления (Δυ) 0,146 см³/г. Определить изменение температуры плав­ления нафталина при увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением (101325 н/м²).

Так как давление дано в н/м², то изменение удельного объема нужно выразить в м³/кг, а теплоту плавления – в Дж/кг. Поскольку Δυ – разность удельных объемов, то вместо мольной теплоты плав­ления можно взять удельную теплоту плавления (Дж/кг):

Изменение температуры плавления при увеличении давле­ния в 100 раз по сравнению с нормальным атмосферным давлением (т.е. при 1,013·10⁷ н/м²) равно 3,453·10^-7 · 1,013·10⁷ = 3,5 ⁰.

Пример 6. Вычислить осмотическое давление 2%-ного раствора глюкозы при 0 °С. Плотность раствора принять равной единице.

Решение. Осмотическое давление вычисляем по формуле:

π = С_МRT.

Концентрация раствора должна быть выражена в кмоль/м³, М (C₆H₁₂O₆) = 180.

В 100 кг 2%-ного раствора содержится 2 кг глюкозы. Плотность данного раствора 1. Следовательно, в 1000 л или в 1 м³ содержится 20 кг глюкозы, что составляет 20/180 кмоль/м³.

Пример 7. Осмотическое давление 0,1 н. раствора сульфата цинка при 0 °С равно 1,59·10⁵ н/м². Определить кажущуюся степень диссоциа­ции соли в данном растворе.

Решение. Концентрация раствора сульфата цинка равна 0,05 моль/л или 0,05 кмоль/м³. Для растворов электролитов приме­няем формулу:

π = iС_МRT, из которой находим i

При диссоциации каждой молекулы соли образуется два иона

т.е. k = 2, так как i = 1 + α, то α = 1 – i = 1,401 – 1 = 0,40, или 40,1 %.

Пример 8. Определить концентрацию раствора глюкозы, если раствор этого вещества при 18 °С изотоничен с раствором, содержа­щим 0,5 моль/л хлорида кальция. Кажущаяся степень диссоциации СаСCl₂ в растворе при указанной температуре составляет 65,4%.

Пример 9. Вычислить давление пара 10%-ного раствора моче­вины СО(NН₂)₂ при 50 °С. Давление паров воды при 50 °С равно 12 320 н/м².

В 100 г 10%-ного раствора мочевины содержится 10 г мочевины и 90 г воды; М (мочевины) = 60; М (воды) = 18. Определяем число молей мочевины (n_a) и воды (n_b) в 100 г 10%-ного раствора

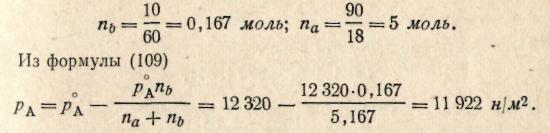
Пример 10. Давление пара чистого ацетона при 20 °С равно 23 940 н/м². Давление пара раствора камфоры в ацетоне, содержаще­го 5 г камфоры на 200 г ацетона при той же температуре, равно 23710 н/м². Определить молярную массу камфоры в растворе ацетона.

Решение. Так как раствор разбавленный, то можно, воспользо­вавшись упрощенной формулой, определить число молей кам­форы

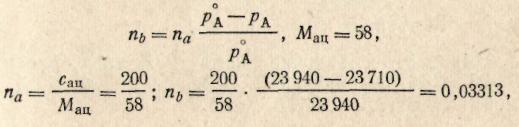
Пример 11. Давление пара раствора, содержащего 5 г едкого натра в 180 г воды при 100 °С, равно 99000 н/м². Вычислить кажу­щуюся степень диссоциации едкого натра в данном растворе.

Решение. Используем формулу:

При 100 °С для воды р_А° = 101325 н/м². Число молей воды n_a = 180/18 = 10; число молей NaOH n_b = 5/40.

При диссоциации каждой молекулы NaОН образуется два иона (А = 2). Для определения α используем уравнение α = 1 – i = 1,837 – 1 = 0,837, или 83,7 %.

Пример 12. Определить атмосферное давление, если 0,1 М раствор хлорида натрия кипит при 99,8 °С? Кажущаяся степень диссоциации 0,1 М раствора NaCl равна 84,4 %. Давление насыщенного пара чистой воды при 99,8 °С равно 100600 н/м².

Решение. При температуре кипения давление пара раствори­теля над раствором равно атмосферному давлению. Следовательно, рассчитав р_А, можно определить и атмосферное давление. Из формулы

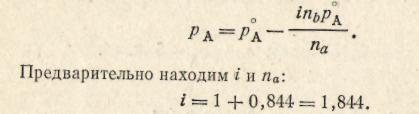
В 1 л 0,1 М раствора хлорида натрия содержится 5,85 г NaCl. Число молей воды (принимаем плотность раствора равной 1) равно:

n_a = (1000 – 5,85)/18 = 55,2 моль.

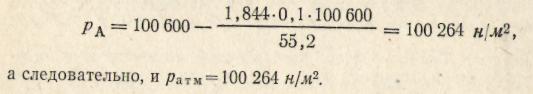
Пример 13. При какой примерно температуре должен замерзать 10 % водный раствор этилового спирта?

Решение. Используем формулу:

Раствор начнет замерзать примерно при -27 °С.

Пример 14. Раствор, содержащий 1,70 г хлорида цинка в 250 г воды, замерзает при -0,23 ⁰С. Определить кажущуюся степень диссоциации хлорида цинка в этом растворе

Пример 15. Определить температуру кипения раствора едкого кали, содержащего в 100 г воды 14 г КОН. Кажущаяся степень диссоциации КОН в растворе равна 60 %.

Решение. Рассчитываем изотонический коэффициент i. Так как при диссоциации каждой молекулы КОН образуется два иона, то k = 2, тогда i = 1 + 0,6 = 1,6. М (КОН) = 56. Определяем моляльность раствора:

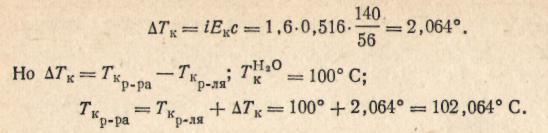
Пример 16. Температура кипения чистого бензола 80,100 °С, а рас­твора, содержащего 0,3020 г дифениламина в 30,14 г бензола, 80,255 °С. Скрытая теплота испарения бензола при температуре его кипения равна 396,0 Дж/г. Вычислить молекулярный вес дифенила­мина в бензоле

Табличное значение М дифениламина 169,23.

Пример 17. Водный раствор, содержащий нелетучее растворенное вещество (неэлектролит), замерзает при -3,5 °С. Определить темпе­ратуру кипения раствора и давление пара раствора при 25 °С. Дав­ление пара чистой воды при 25 °С 3167,2 н/м².

Решение. Понижение температуры замерзания раствора равно:

0 – (-3,5) = 3,5 °;

Е₃ и Е_к находим по справочнику. По формуле определяем моляльную концентрацию рас­твора

Для вычисления давления пара раствора преобразуем форму­лу:

Пример 18. Плотность твердого фенола 1072 кг/м³, жидкого 1056 кг/м³, теп­лота его плавления 1,044·10⁵ Дж/кг, температура замерзания 314,2 К. Вычислите dp/dT и температуру плавления фенола при 5,065·10⁷ Па.

Решение. По уравнению Клапейрона-Клаузиуса рассчитываем dp/dT

Чтобы вычислить температуру плавления при заданном внешнем дав­лении, принимаем, что dT/dp в интервале давлений 1,0132·10⁵-5,065·10⁷ Па – величина постоянная, равная 4,214·10^-8 К/Па. Тогда

Пример 19. Вычислите среднюю теплоту испарения СН₄ в интервале тем­ператур от 88,2 до 113 К, используя следующие данные:

lg(p₁/p₂) = (ΔH_ф.п./2,3R)[(T₂ – T₁)/T₂T₁]

по уравнению:

lgp = A – B/T, из которого следует, что зависимость lgp от 1/T выражается прямой линией. Теплоту испарения можно определить по тангенсу угла наклона прямой, который равен: tgα = -ΔH_исп./2,3R. Вычисляем для приведенных данных lgp и 1/T:

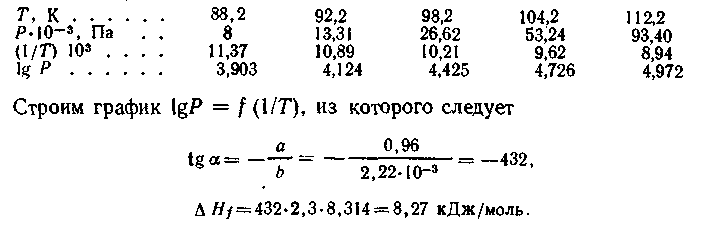
Этот результат более точен, чем предыдущий, так как вычислен на ос­новании пяти опытов (истинное значение теплоты испарения метана при нормальной температуре кипения 8,19 кДж/моль).

Пример 20. Вычислите S⁰(H₂O_пар), если S⁰(H₂O_ж) = 69,96 Дж/(моль·К).

Решение. Для расчета представим себе процесс превращения жидкой воды в пар под давлением 1,0132·10⁵ Па, который состоит из двух стадий: 1) равновесное испарение под давлением, равным давле­нию насыщенного пара, ΔS_исп.; 2) равновесное сжатие ΔS_сж. насыщен­ного пара до давления 1 атм. Тогда

Для определения ΔН_исп. по справочнику находим теплоты обра­зования воды для разных агрегатных состояний при 298 К:

и давление насыщенного пара воды равно 3,167·10³ Па. После подстанов­ки чисел и вычислений получаем

и абсолютная энтропия пара составит:

Пример 21. При 268,2 К давление насыщенного пара твердого бензола 2279,8 Па, а над переохлажденным бензолом (жидким) 2639,7 Па. Вы­числите изменение энергии Гиббса в процессе затвердевания 1 моль переохлажденного бензола при указанной температуре (пары бензола считать идеальным газом) и укажите, обратимый или необратимый процесс.

Решение. Поскольку изменение энергии Гиббса не зависит от пути процесса, принимаем, что процесс затвердевания состоит из трех стадий: 1) обратимое испарение жидкого бензола при давлении 2639,7 Па; 2) обратимое расширение паров до давления 2279,8 Па; 3) обратимая конденсация паров в твердую фазу. Тогда

как 1-я и 3-я стадии протекают при р и Т = const обратимо, то ΔG₁ = ΔG₃ = 0,

Результат указывает на необратимость данного процесса.

Пример 22. Давление насыщенного водяного пара при 428,2 К равно 54,3·10⁴ Па, а удельный объем пара 0,3464 м³/кг. Рассчитайте фугитивность воды, находящейся при 428,2 К в равновесии со своим насы­щенным паром.

Решение. Фугитивность жидкости равна фугитивности ее насыщенного пара, а так как давление отно­сительно невелико, фугитивность насыщенного пара можно вычислить по уравнению

Пример 23. Давление водяного пара раствора, содержащего нелетучее раст­воренное вещество, на 2 % ниже давления пара чистой воды. Опреде­лите моляльность раствора

Приняв за 100 давление пара чистого растворителя р₁⁰ и подставив 98 вместо р₁, получим

Для определения моляльности рассчитаем число молей растворен­ного вещества на 1000 г воды по уравнению:

x₂ = n₂/(n₂ + n₁),

где n₁ – число молей воды (1000/18 = 55,55); n₂ = m.

После подстановки значений в уравнение получаем:

0,02 = m/(55,55 + m), откуда m = 1,134.

Пример 24. Вычислите эбуллиоскопическую постоянную воды. Теп­лота испарения равна 40,685 кДж/моль.

Решение. Эбуллиоскопическую константу вычисляем по урав­нению:

Пример 25. Определите температуру кипения водного раствора, содержаще­го 0,01 моль нелетучего вещества в 200 г воды. К_э = 0,512 град/моль.

Решение. Вычисляем моляльность раствора:

По уравнению вычисляем температуру кипения раствора:

ΔТ_к. = К_э.m

Пример 26. Понижение температуры замерзания водного раствора иссле­дуемого вещества составляет 1,395 К, а бензольного – 1,280 К. Чем объясняется различие в ΔT, если моляльности растворов одинаковы? Какие величины, характеризующие состояние вещества в растворе, можно получить из этих данных? Для бензола К_кр = 5,16, град/моль; для воды К_кр = 1,86 град/моль.

Решение. Различия в температурах замерзания можно объяс­нить тем, что вещество в водном растворе дисссоциирует, а в бензоль­ном – не диссоциирует. Можно вычислить коэффициент Вант-Гоффа i.

ΔТ_з. = К_кр.m или ΔТ_з. = iК_кр.m.

Зная числовое значение i, можно сделать, согласно уравнению:

i = 1 + α(v – 1),

предположение о числе частиц, на которые распадается молекула растворенного вещества, и о степени диссоциации. Согласно сделанным предположениям

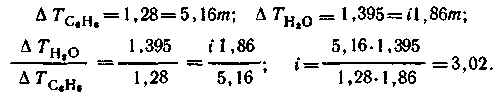
Если молекула, распадаясь, дает две частицы, то даже при α = 1 i = 2. Полученное значение i > 2 показывает, что v > 2.

Вычисляем степень диссоциации, предполо­жив, что v = 3; тогда 2,52 = 1 + α (3 – 1), откуда α = 0,76. Если v = 4, α = 0,50 и т. д.