Законы термодинамики

Пример 1. Определить теплоту, которую отдадут 100 кг паров метилового спирта при охлаждении от 200 до 100° С при нормальном давлении.

Решение. Количество выделяемой теплоты можно рассчитать двумя способами:

1. используя значение средней (удельной) теплоемкости между 200 и 100 ⁰С (с учетом массы паров спирта);

2. определяя среднюю теплоемкость паров метилового спирта от 0 до 200 °C и от 0 до 100 °С. Подсчитать отдельно относительные количества теплоты при 200 °С и при 100 °С (с учетом массы паров) и вычесть одно из другого. Полученное количество теплоты соответствует отданной 100 кг паров СН₃ОН при их охлаждении.

Воспользуемся вариантом 2. Из таблицы находим для СН₃ОН средние мольные теплоемкости при нормальном давлении для 200 и 100 °С(57,0 кДж/кмоль·град и 53,7 кДж/кмоль·град).

с = С/М

Пример 2. Определить теплоту, поглощаемую при нагревании 100 г двуокиси углерода от 15 до 1000 °С при постоянном объеме, если

Решение. Используем формулу (температуру можно взять в градусах Цельсия):

(для одного моля).

Определяем число молей СО₂. Оно равно 100/44:

Пример 3. Рассчитать среднюю мольную теплоемкость водорода в интервале температур 400-500 °С, если

Решение. Используем формулу (значения температур оставляем в °С):

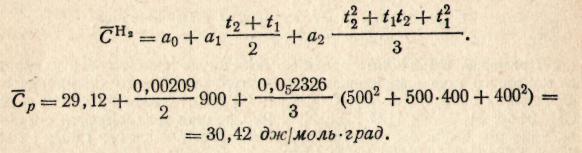
Пример 4. Средняя удельная теплоемкость двуокиси углерода в интервале от 0 до 1000° С выражается формулой

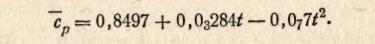
Рассчитать истинную мольную и удельную теплоемкости для дву­окиси углерода при 200 °С.

Решение. В соответствии с формулой (50)

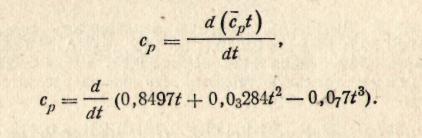
В результате дифференцирования и подстановки t = 200 ⁰С получим

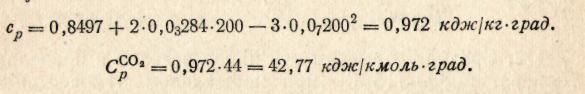
Пример 5. Средняя мольная теплоемкость кислорода при посто­янном давлении в интервале температур от 0 до 1500 °С выражается формулой

Определить средние мольную, удельную и объемную теплоемко­сти при постоянном давлении в интервале температур от 0 до 1000 °С.

Решение. Рассчитаем среднюю мольную теплоемкость от 0 до 1000 °С:

Рассчитаем среднюю удельную теплоемкость по формуле:

Определим объемную теплоемкость по формуле:

Пример 6. Определить среднюю объемную теплоемкость влажно­го коксового газа в интервале температур от 0 до 20 °С, имеющего следующий состав (об. %): СО₂ 2,64; О₂ 0,79; С_mН_n 2,07; СО 5,08; СН₄ 24,66; Н₂ 58,00; Н₂О 2,30; N₂ 4,46. Средние теплоемкости состав­ляющих его газов соответственно равны (кДж/м³·град): 1,697; 1,303; 2,082; 1,274; 1,504; 1,295; 1,455; 1,270.

Решение. Среднюю объемную теплоемкость указанной смеси газов в интервале температур 0-20 °С можно рассчитать по фор­муле:

С_об = 1/100 (а₀С₁ + b₀C₂ + …)

Пример 7. Вычислить удельную теплоемкость сплава состава (вес. %): Вi 50,7; Рb 25,0; Си 10,1; 5п 14,2; если с_р²⁹⁸ (кДж/кг·град): для висмута 0,122, свинца 0,129, кадмия 0,231, олова 0,221.

Решение. Удельную теплоемкость сплава рассчитаем по фор­муле:

C = ΣnC_i

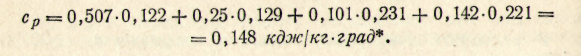
Пример 8. Определите работу изобарного обратимого расширения 3 моль идеального газа при его нагревании от 298 до 400 К.

Решение. Работу изобарного расширения определяем по урав­нению:

W = nR(T₂ – T₁)

Пример 9. Определите работу испарения 3 моль метанола при нормальной температуре кипения.

Решение. Нормальная температура кипения – это темпера­тура кипения при внешнем давлении, равном 1,0133 · 10⁵ Па. Нор­мальную температуру кипения находим в справочнике Тн.т.к. = 337,9 К. Работу определим по уравнению,

W = p(v₂ – v₁)

так как испарение происходит при постоянном давлении. Конечный объем приближенно можно определить по закону идеального газообразного состояния

В первом приближении объемом жидкости v₁ можно пренебречь, так как объем жидкости при температурах, далеких от критической, значительно меньше объема пара. Тогда

Пример 10. Определите работу изотермического обратимого расширения 3 моль водяного пара от 0,5·10⁵ до 0,2·10⁵ Па при 330 К. Водяной пар при таких параметрах подчиняется закону идеального газообраз­ного состояния.

Решение. Работу определим по уравнению:

W = nRTln(p₁/p₂)

Пример 11. Определите работу адиабатического обратимого расширения 3 моль аргона от 0,05 до 0,50 м³. Начальная температура газа 298 К.

Решение. Для определения работы адиабатического расшире­ния воспользуемся уравнением:

W = nRT/(γ- 1) · [1 – (v₁^γ-1/ v₂^γ-1)].

Величину γ определим из С_р и С_v. Аргон – одноатомный газ. Следовательно, его изохорная тепло­емкость на основании молекулярно-кинетической теории идеальных газов равна С_v =3/2 R = 1,5·9,3143 = 12,4715 Дж/(моль·К):

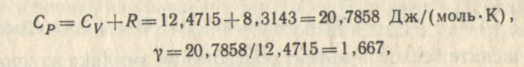
отсюда