3.4. Классификация проекции по характеру искажений

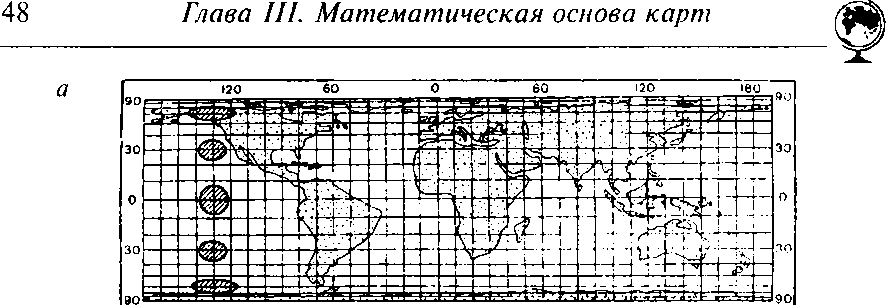
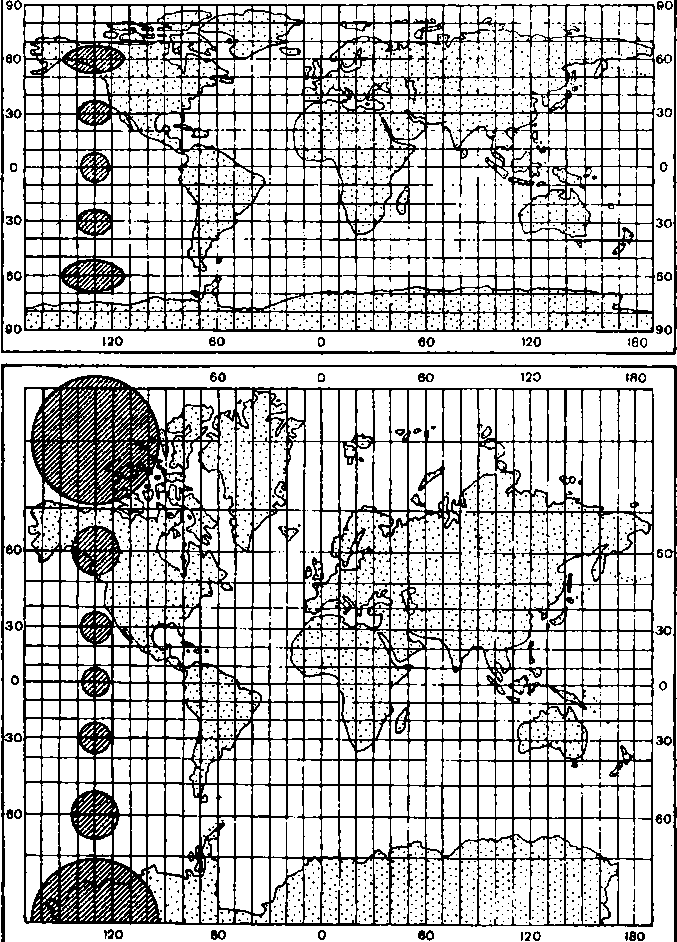
Равновеликие проекции сохраняют площади без искажений. Та-кие проекции удобньї для измерения площадей обьектов, однако, в них значительно нарушеньї угльї и формьі, что особенно заметно для больших территории. Например, на карте мира (рис. 3.5я) при-полярньїе области вьіглядят сильно сплющенньїми.

Равноугольньїе проекции оставляют без искажений угльї и фор-мьі контуров, показанньїх на карте (ранее такие проекции назива­ли конформними). Злементарная окружность в таких проекциях всегда остается окружностью, но размерьі ее сильно меняются (рис. 3.5в). Такие проекции особенно удобньї для определения на­правлений и прокладки маршрутов по заданному азимуту, позто-му их всегда используют на навигационньїх картах. Зато картьі, составленньїе в равноугольньїх проекциях, имеют значительньїе искажения площадей.

Равнопромежуточньїе проекции — произвольньїе проекции, в которьіх масштаб длин по одному из главньїх направлений посто-янен и обьічно равен главному масштабу картьі. Соответственно различают проекции равнопромежуточньїе по меридианам — в них без искажений остается масштаб вдоль меридианов, и равнопроме­жуточньїе по параллелям — в них сохраняется постоянньїм мас­штаб вдоль параллелей. В таких проекциях присутствуют искажения площадей и углов, но они как бьі уравновешиваются (рис. 3.56).

Произвольньїе проекции — зто все остальньїе видьі проекции, в которьіх в тех или иньїх произвольньїх соотношениях искажаются и площади, и угльї (формьі). При их построении стремятся найти наиболее вьігодное для каждого конкретного случая распределе-ние искажений, достигая как бьі некоторого компромисса. Скажем, вьібирают проекции с минимальньїми искажениями в центральной части картьі, «сбрасьівая» все сжатия и растяжения к краям.

3.5. Классификация проекции по виду нормальной картографической сетки

Вспомогательньїми поверхностями при переходе от зллипсои­да или шара к карте могут бьіть плоскость, цилиндр, конус, серия конусов и некоторьіе другие геометрические фигурьі.

Цилиндрические проекций — проектирование шара (зллипсои­да) ведется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость (рис. 3.6). Если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по зкватору (или сечет его по па-раллелям), то проекция назьівается нормальной (прямой) цилинд-рической. Тогда меридианьї нормальной сетки предстают в виде равноотстоящих параллельньїх прямьіх, а параллели — в виде пря-мьіх, перпендикулярних к ним. В таких проекциях меньше всего искажений в тропических и призкваториальньїх областях.

Если ось цилиндра расположена в плоскости зкватора, то зто — поперечная цилиндрическая проекция. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и следовательно, в такой проекций наиболее вьігодно изображать территории, вн-тянутьіе с севера на юг. В тех случаях, когда ось вспомогательного цилиндра расположена под углом к плоскости зкватора, проекция назьівается косой цилиндрической. Она удобна для вьітянутьіх тер­ритории, ориентированньїх на северо-запад или северо-восток.

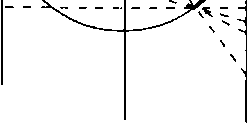
Конические проекций — поверхность шара (зллипсоида) проек-тируется на поверхность касательного или секущего конуса, после чего она как бьі разрезается по образующей и разворачивается в плоскость (рис. 3.7). Как и в предьідущем случае, различают нор­мальную (прямую) коническую проекцию, когда ось конуса совпа­дает с осью вращения Земли, поперечную коническую — ось конуса лежит в плоскости зкватора и косую коническую — ось конуса на-клонена к плоскости зкватора.

В нормальной конической проекций меридианьї представляют собой прямьіе, расходящиеся из точки полюса, а параллели — дуги концентрических окружностей. Воображаемьій конус каса­ется земного шара или сечет его в районе средних широт, позто-му в такой проекций удобнее всего картографировать территории России, Канади, США, внтянутне с запада на восток в средних широтах.

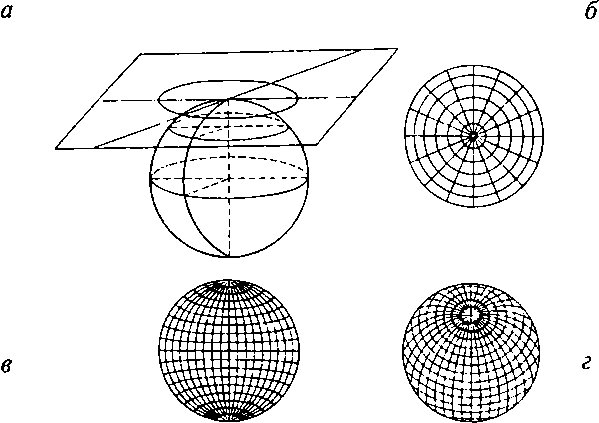
Азимутальньїе проекций — поверхность земного шара (зллип­соида) переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция (рис. 3.8а). Парал­лели в ней являются концентрическими окружностями, а мериди­аньї — радиусами зтих окружностей. В зтой проекций всегда кар-тографируют полярнне области нашей и других планет.

4 - 4886

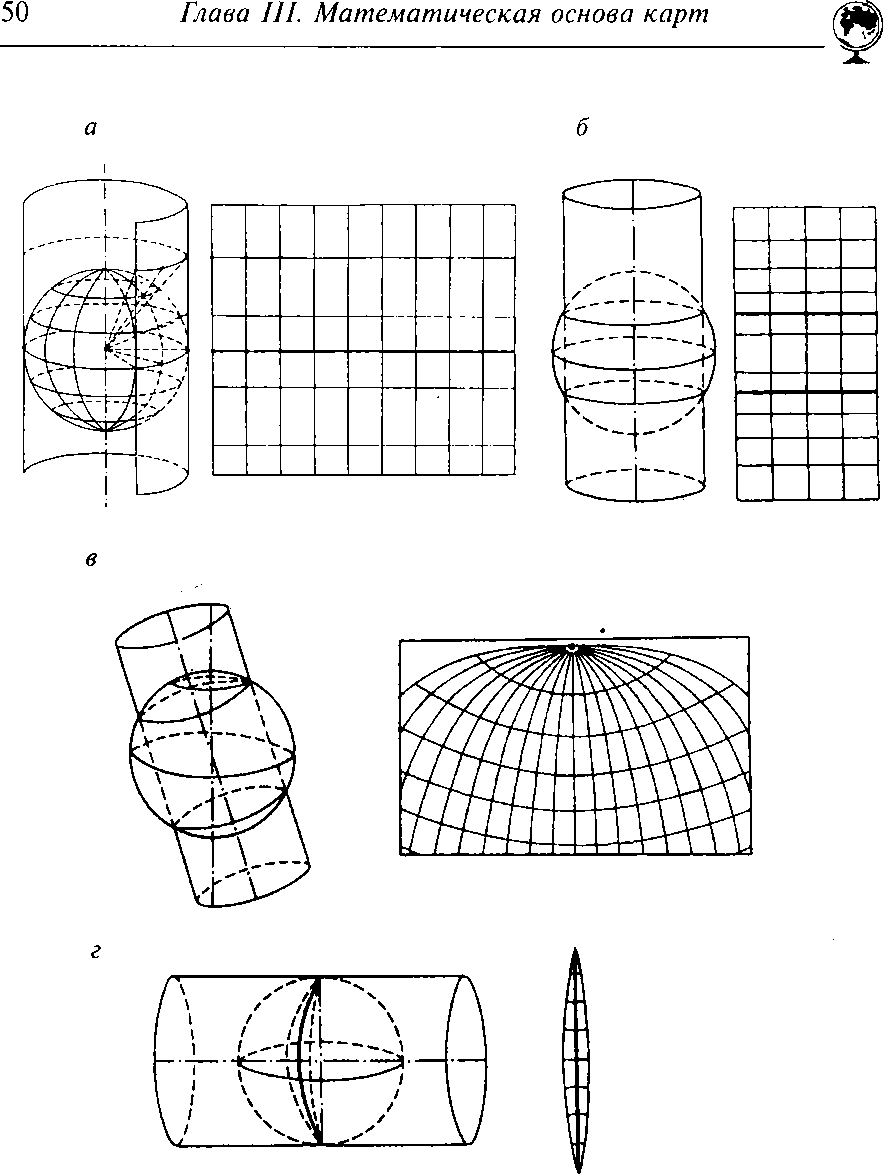
а — развертка нормальной цилиндрической проекций (проектирование на касательньїй цилиндр); б — нормальная цилиндрическая проекция на секу-щий цилиндр; в -т- косая цилиндрическая проекция на секущем цилиндре; г— поперечная цилиндрическая проекция на касательном цилиндре (осо-бенно удобна для проектирования геодезических зон).

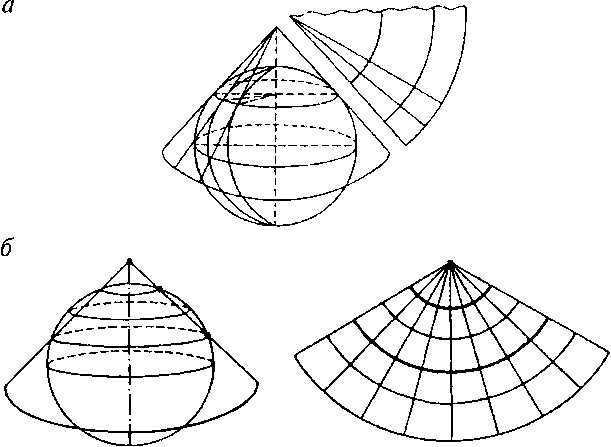
а — проекция на касательньїй конус и развертка; б — проекция на секущий конус и развертка.

а — нормальная или полярная проекция на плоскость; б — сетка в полярной проекций; в — сетка в поперечной (зкваториальной) проекций; г — сетка в косой азимутальной проекций.

Если плоскость проекций перпендикулярна к плоскости зква­тора, то получается поперечная (жваториальная) азимутальная проекция. Она всегда используется для карт полушарий (рис. 3.8#). А если проектирование вьіполнено на касательную или секущую вспомогательную плоскость, находящуюся под любьш углом к плоскости зкватора, то получается косая азимутальная проекция (рис. 3.8г).

Можно показать, что азимутальньїе проекций являются пре-дельньїм случаем конических, когда угол при вершине конуса принимается равньїм 180°.

Среди азимутальних проекций вьіделяют несколько их разно-видностей, различающихся по положенню точки, из которой ве-дется проектирование шара на плоскость (рис. 3.9).

Положение точки проектирования относительно шара (зллипсоида)

В центре шара

На противоположном конце диаметра

За пределами шара на продол-жении диаметра В бесконсчности

Название азимутальной проекций

Гномоническая

Стереографическая

Внешняя Ортографическая

Плоскость проектирования

Внешняя Стереографическая

Ортографическая

Рис. 3.9. Положение центра проектирования для азимутальних проекций.

У словньїе проекций — проекций, для которьіх нельзя подобрать простих геометрических аналогов. Их строят, исходя из каких-либо заданньїх условий, например желательного вида географической сетки, того или иного распределения искажений на карте, задан-ного вида сетки и др. В частности, к условньїм принадлежат псевдо-цилиндрические, псевдоконические, псевдоазимутиальньїе и другие про­екций, полученньїе путем преобразования одной или нескольких исходньїх проекций. На рис. 3.10 приведеньї видьі сеток описанньїх вьіше и некоторьіх условньїх проекций.

Псевдоцилиндринеские проекций — проекций, в которьіх парал­лели — прямьіе линии (как и в нормальних цилиндрических про­екциях), средний меридиан — перпендикулярная им прямая, а остальньїе меридианьї — кривьіе, увеличивающие свою кривизну по мере удаления от среднего меридиана. Чаще всего зти проекций применяют для карт мира и Тихого океана.

Псевдоконические проекций — такне, в которьіх все параллели изображаются дугами концентрических окружностей (как в нор­мальних конических), средний меридиан — прямая линия, а ос­тальньїе меридианьї — кривне, причем кривизна их возрастает с

у далением от среднего меридиана. Применяются для карт России, Евразии, других материков.

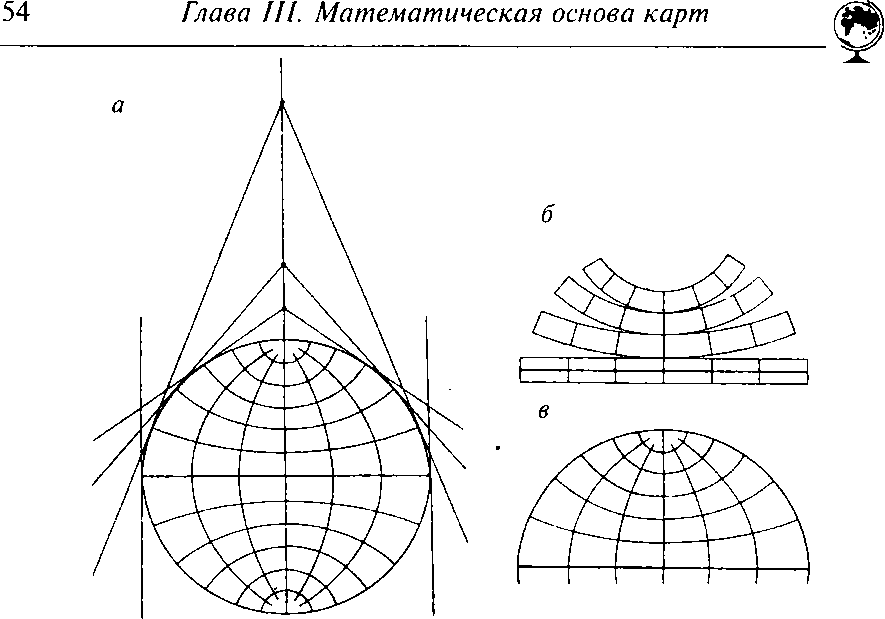
Поликонические проекции — проекции, получаемьіе в результа­те проектирования шара (зллипсоида) на множество конусов. В нормальних поликонических проекциях параллели представленьї дугами зксцентрических окружностей, а меридианьї — кривьіе, симметричньїе относительно прямого среднего меридиана (рис. 3.11). Чаще всего зти проекции применяются для карт мира.

Псевдоазимутальньїе проекции — видоизмененньїе азимуталь-ньіе проекции. В полярньїх псевдоазимутальньїх проекциях парал­лели представляют собой концентрические окружности, а мери­дианьї — кривьіе линии, симметричньїе относительно одного или двух прямьіх меридианов. Поперечньїе и косьіе псевдоазимуталь­ньїе проекции имеют общую овальную форму и обьічно применя­ются для карт Атлантического океана или Атлантического океана вместе с Северньїм Ледовитьім.

Многогранньїе проекции — проекции, получаемьіе путем про­ектирования шара (зллипсоида) на поверхность касательного или секущего многогранника (рис. 3.12). Чаще всего каждая грань пред­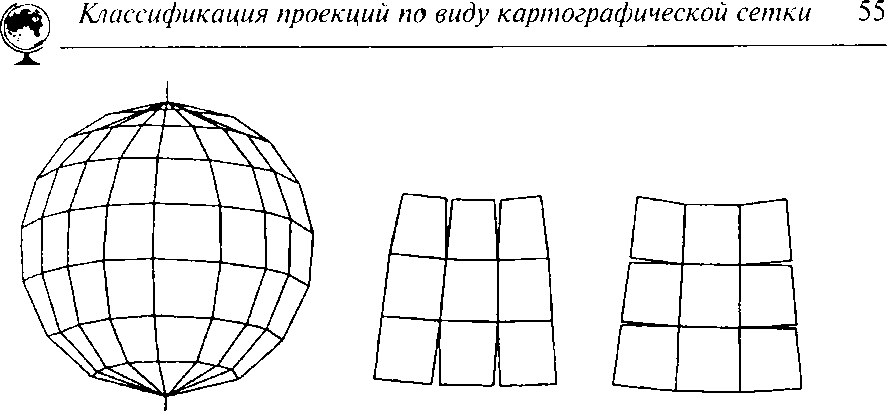

ставляет собой равнобочную трапецию, хотя возможньї и иньїе вариантьі (например, шестиугольник, квадрат, ромб). Разновид-ностью многогранньїх являются многополосньїе проекции, причем полосьі могут «нарезаться» и по меридианам, и по параллелям. Такие проекции вьігодньї тем, что искажения в пределах каждой грани или полосьі совсем невелики, позтому их всегда использу-ют для многолистньїх карт. Рамка каждого листа, составленного в многогранной проекции, представляет собой трапецию, образо-ванную линиями меридианов и параллелей. За зто приходится «рас-плачиваться» — блок листов карт нельзя совместить по общим рамкам без разрьівов.

Надо отметить, что в наши дни для получения картографи­ческих проекции не пользуются вспомогательньїми поверхностя-ми. Никто не помещает шар в цилиндр и не надевает на него конус. Зто всего лишь геометрические аналогии, позволяющие понять геометрическую суть проекции. Изьіскание проекции ВЬІ-полняют аналитически. Компьютерное моделирование позволяет достаточно бьістро рассчитать любую проекцию с заданньїми па­раметрами, автоматические графопостроители легко вьічерчива-ют соответствующую сетку меридианов и параллелей, а при необ-ходимости — и карту изокол.

Существуют специальньїе атласьі проекции, позволяющие по-добрать нужную проекцию для любой территории. В последнее время созданьї злектронньїе атласьі проекции, с помощью которьіх лег­ко отьіскать подходящую сетку, сразу оценить ее свойства, а при необходимости провести в интерактивном режиме те или иньїе модификации или преобразования.