Ограничения на сложность изображения

1.     Контур, ограничивающий поверхность аппроксимируется ломаной линией. Тогда хранятся и преобразуются только точки, являющиеся координатами вершин ломаной линии. Остальные точки контура восстанавливаются после проведения всех геометрических преобразований с координатами вершин. 

2.     Все изображаемые поверхности являются плоскими. Следовательно, изображаемое тело является многогранником, в общем случае произвольной формы. Тогда возможно применение быстрой тоновой заливки плоских граней специальными алгоритмами, т.к. тон не изменяется в пределах отдельной грани. Тон заливки изменяется только от грани к грани в соответствии с положением источника освещенности и удаленности от него. 

3.     Изображаемые тела являются выпуклыми. Тогда плоская грань невидима, если нормаль к ней образует угол больший 90^o с направлением к точке зрения. Тогда объект сложной формы представляется объединениями его выпуклых частей, у которых из рассмотрения сразу исключены все задние, т.е. невидимые грани. 

После удаления невидимых поверхностей в данной структуре появляется указание о видимости каждой ее вершины.

Если некоторая вершина в этой структуре полностью невидима, то невидимы и все ее вершины нижних уровней.

7. Тесты пересечения на плоскости.

Пересечение двух прямых на плоскости

Пусть плоскости заданны уравнениями: 

определяется как решение матричного уравнения:

Если ,то прямые параллельны. Дополнительное условие определяет совпадают ли параллельные прямые или нет. В противном случае точка пересечения определяется как:

Пересечение двух отрезков в плоскости

Пусть заданы две прямые, пересекающиеся в точке . На каждой из них своими начальной и конечной точками заданы отрезки , где

Тогда два отрезка  пересекаются в , если:

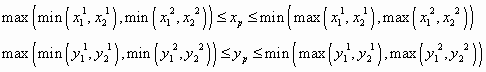
8. Пересечение плоскости и прямой.

Пересечение плоскости и прямой

Плоскость задана уравнением , где  - вектор, перпендикулярный заданной плоскости (направляющий вектор) длины , а D - смещение плоскости от начала координат, где  - расстояние плоскости от начала координат.

Уравнение плоскости описывает множество ее точек с координатами (x;y;z). Перепишем его в нормированном виде:

Если D = 0, то заданная плоскость проходит через начало координат, а ее уравнение называется уравнением плоскости без смещения. Фактически плоскость может быть представлена множеством векторов, проведенных их начала координат в точки , перпендикулярных направляющему вектору плоскости . Другими словами, это векторы, расстояние от которых до заданной плоскости равно нулю. Это утверждение можно записать как:

Заметим, что .

С другой стороны, прямая, проходящая через две точки  имеет длину  . Ее проекция на ось Х имеет длину , и определяется направляющим углом относительно оси ОХ. Аналогично . Тогда значения  представляют собой проекции единичного направляющего вектора прямой на оси координат.

Расстояние точки  до плоскости есть величина  с учетом расстояния до самой плоскости от начала координат. Тогда длина r от точки  до точки пересечения с плоскостью  есть величина, полученная из соотношения:

Величина определяется как угол между направляющим вектором прямой и нормалью к плоскости.

Тогда

Координаты точки пересечения прямой с плоскостью определяется из соотношений:

9. Тесты принадлежности. Тест видимости

Тесты принадлежности.

Эти тесты проверяют, лежит ли точка Р внутри плоского многоугольника .

Тест 1.

Пусть a_i - угол между отрезками P_iP_i+1 и P_i+1P_i+2. Тогда точка P находится вне многоугольника F, если  и внутри, если

Рисунок 10.1. Тест принадлежности 1

Тест 2.

Пусть R - луч из точки Р, проходящий через F, но не содержащий ни одной его вершин P_i. Тогда, если число пересечений F и R нечетно, то Р внутри многоугольника, а если четно, то Р находится снаружи.

Тест видимости

Этот тест применяется к трехмерным телам. С помощью него выявляются задние (невидимые) грани тела. Из уравнения плоскости для каждрй грани определяются координаты ее направляющего вектора (нормаль к плоскости), а затем определяется угол между направляющим вектором и линией проецирования. Грань невидима, если угол между ними больше 90⁰. можно записать как:

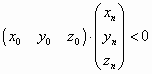
где  - точка зрения, а  - нормаль к плоскости.

10. Тесты глубины.