Задачи компьютерной графики и ее место среди других методов обработки информации.
Обработка информации, представленной в виде изображений, на ЭВМ имеет множество разновидностей и массу практических приложений. Эту область обработки информации обычно принято разделять на три направления: машинную графику, обработку изображений и распознавание изображений.
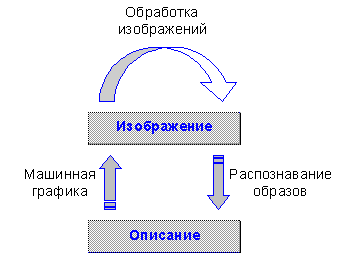
Задача машинной графики — воспроизведение изображений в тех случаях, когда исходной является информация неизобразительной природы; Термин интерактивная машинная графика относится к устройствам и системам, в которые пользователь вводит исходные данные, сформулированные в терминах порождаемого визуального отображения (например, требуется провести на экране прямую между двумя точками, указанными пользователем).
Обработка изображений связана с решением таких задач, в которых и входные, и выходные данные являются изображениями. Одним из примеров служат системы передачи изображений.
Задачей распознавания изображений является применение методов, позволяющих либо получить некоторое описание изображения, поданного на вход системы, либо отнести это изображение к некоторому определенному классу. Распознавание зрительных образов представляет собой, в некотором смысле, обратную задачу машинной графики.
Основные направления компьютерной графики. Основные структурные элементы системы машинной графики.
Выделим некоторые направления компьютерной графики (отметив, что это выделение достаточно условно):
иллюстративное, которое можно понимать расширительно, начиная с пояснений (визуализации) результатов эксперимента и кончая созданием рекламных роликов;
саморазвивающее - компьютерная графика должна обслуживать свои потребности, расширяя свои возможности и совершенствуя их;
исследовательское, в котором инструментарий компьютерной графики начинает играть роль, во многом подобную той, которую в свое время сыграл микроскоп.
Компьютерная графика и геометрия базируются на таких дисциплинах, как различные разделы геометрии (аналитическая, начертательная, дифференциальная, проективная, прикладная), программирование для ЭВМ, элементы вычислительной математики, понятия о формальных языках, применимых в общенйи человека и Машины.
Виды данных, представленных в форме изображений.
Класс 1: тоновые и цветные изображения
В класс 1 входят изображения, имеющие вид обычных телевизионных изображений. Они обеспечивают довольно точное воспроизведение «реальности» и представляются матрицами с целочисленными элементами (для обозначения последних обычно используют термины элемент изображения, пиксел и пэл). Цветные изображения могут представляться либо при помощи трех матриц (для красного, зеленого и синего цветов), либо с помощью одной матрицы таким образом, что отдельные биты каждого элемента представляют различные цвета. Поскольку человеческий глаз обычно не в состоянии различать уровни освещенности, отличающиеся друг от друга менее чем на 1%, то для представления цветного изображения достаточно затрачивать по одному байту на цвет на пиксел.
Класс 2: двухуровневые или представляемые в нескольких «цветах» изображения
Изображение книжной страницы служит типичным примером представителя класса 2 — двухуровневого (черно-белого) изображения. Подобные изображения можно представлять матрицами, затрачивая по одному биту на элемент, а также и в виде «карт», так как на этих изображениях имеются хорошо различимые области одного цвета. Именно поэтому мы объединяем в один класс изображения, представляемые в нескольких «цветах», и двухуровневые изображения, несмотря на то, что представление с затратой одного бита на элемент матрицы удачно лишь для двухуровневых изображений.
Класс 3: непрерывные кривые и линии
Примерами изображений класса 3 служат контуры областей, сигналы и диаграммы (графики). Соответствующие данные являются последовательностями точек, допускающих представление через их координаты х, у. Однако этот метод представления довольно неэффективен, причем то же самое относится к представлению, основанному на использовании разностей значений координат соседних точек. Более эффективным является представление с помощью цепных кодов, при использовании которых вектору, соединяющему две соседние точки, ставится в соответствие один символ, принадлежащий некоторому конечному множеству. Еще более эффективный способ представления заключается в применении дифференциального цепного кода, предусматривающего -кодирование каждой точки разностью двух последовательных абсолютных кодов. В этом случае все еще сохраняется восемь значений (0, ±1, ±2, ±3 и 4), однако вероятности их появления неодинаковы. Можно ожидать, что при кодировании гладких кривых значения 0 и ±1 будут появляться много чаще, чем все остальные, а значение 4 — чрезвычайно редко. Поэтому для представления различных направлений можно воспользоваться каким-либо из кодов с переменной длиной. Приведем один из возможных вариантов кодирования словами с переменной длиной при использовании дифференциального цепного кода.
Класс 4: точки или многоугольники
Изображения класса 4 состоят из множеств отдельных точек, отстоящих друг от друга столь далеко, что для их представления цепным кодом пользоваться нельзя. Вместо него следует применять матрицу, содержащую их координаты x, у. Соответствующая аппаратура отображения позволяет соединять точки прямыми или простыми кривыми. Различие между классами 4 и 3, как и между предыдущими классами, довольно неопределенно и приобретает смысл лишь при обращении к способу, используемому для представления изображения.
Во многих прикладных задачах используется одна из следующих форм представления.
Аппроксимация -поверхности многогранниками; грани — обычно треугольники; после проектирования изображение состоит из многоугольников. (триангуляция)
Криволинейная аппроксимация поверхности; на поверхности тела вычерчивается ряд кривых, описания которых затем используются для получения проекций, воспроизводимых в виде изображений класса 3.
Аппроксимация участками поверхности высшего порядка; этот способ аналогичен способу 1, за исключением того, что в качестве элементов, образующих поверхность объекта, используются не плоские многоугольники, а участки поверхности высшего порядка.
Во всех случаях положение объекта определяется некоторым небольшим числом точек и потому изображения класса 4 действительно представляют наибольший интерес для машинной графики.
Понятие изображения.
В наиболее общем случае изображение можно определить как некоторое множество точек плоскости, каждая из которых обладает своим цветом, и удовлетворяет нижеизложенным критерия.
Плоскость ограничена по площади. Как правило, предполагается, что выделена прямоугольная область плоскости.
Множество точек, составляющих поверхность плоскости, является конечным. Следовательно, точки такой плоскости всегда можно перечислить. Это важно, т.к. множество точек видеоизображения надо адресовать.
Множество различных цветов точки также является конечным.
Таким образом данное (техническое) определение изображения реально удовлетворяет широко распространенному устройству отображения – растровому дисплею.
Понятие о структуре изображения. Основные графические элементы (примитивы).
Изображение представляет собой образ некоторого исходного объекта. Исходный объект может быть материальным объектом, реально существующим в природе. Изображение представляет собой некоторый объект, обладающий структурой. Содержательно, такая структура образована одноцветными областями различной формы, накрывающими все поле изображения.
Структура определяется множеством ее элементов и взаимосвязями между ними. Структура изображается графом, где вершины являются ее элементами, а ребра – связями ее элементов.
Следовательно, для построения графического изображения некоторой модели требуется:
1) определить поле изображения;
2) определить совокупность примитивов, соответствующих данной модели;
3) определить логические взаимосвязи примитивов в виде некоторого графа.
Все эти требования имеет специальное название – графическая модель объекта.