2. Общая задача линейного программировании (лп). Матричная форма задачи лп. Графический метод решения задачи лп.

В общем случае задачу линейного программирования можно сформулировать следующим образом: даны система линейных уравнений

 

(где можно считать, что  , изменяя, если нужно, знак в соответствующем уравнении ) и линейная функция

.                                                      

Требуется среди неотрицательных решений системы   , найти такое решение, для которого линейная функция   принимает наименьшее значение.

Функция, экстремальное значение которой требуется отыскать, называется целевой функцией. Система равенств и неравенств называется системой ограничений. Всякий набор значений переменных, то есть вектор X значений, X (x1 ,x2 , xn ) называется планом задачи. План называется допустимым планом, если он удовлетворяет системе ограничений. Обычно (но не всегда) множество допустимых планов бесконечно. На разных планах целевая функция принимает различные значения. Задача линейного программирования требует, чтобы среди всех допустимых планов был найден тот план, на котором целевая функция достигает искомого экстремального значения (максимального и минимального, в зависимости от конкретной задачи). Такой план называется оптимальным планом. Значение целевой функции на оптимальном плане называется оптимумом. Решить задачу линейного программирования – значит найти ее оптимальный план и оптимум.

Матричная форма выглядит следующим образом

Как обычно, посредством A обозначим матрицу системы ограничений:

Посредством X и B обозначим соответственно столбец неизвестных задачи (план задачи) и столбец свободных членов (правых частей системы ограничений):

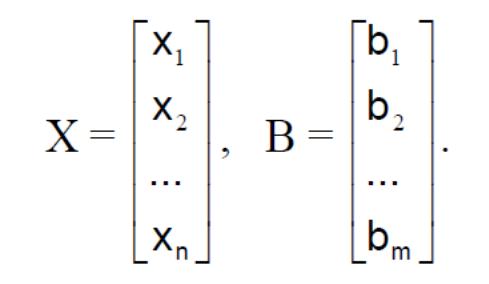
Наконец, посредством C обозначим вектор-строку коэффициентов целевой функции:

Тогда задача производственного планирования запишется в следующей форме

Решение задачи линейного программирования графическим методом включает следующие этапы:

На плоскости X₁0X₂ строят прямые.

Определяются полуплоскости.

Определяют многоугольник решений;

Строят вектор N(c₁,c₂), который указывает направление целевой функции;

Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.

Вычисляют координаты точки и значение целевой функции в этой точке.

3.Задачи постоптимизационного анализа. Теневая цена ресурса и ценовой анализ.

После математического решения задачи линейного программирования, расчета ее оптимального плана и оптимума, необходимо проанализировать полученные результаты. Такой анализ называют постоптимизационным. Общая задача такого анализа – определить устойчивость полученного решения к тому или иному изменению ситуации, к изменению условий задачи, а также оценить чувствительность решения к изменению конкретных численных значений тех или иных параметров ситуации. Обычно результаты анализа охватывают несколько разделов. Важность тех или иных разделов зависит от конкретной экономической ситуации, описываемой в задаче.

Теневая цена ресурса

Во-первых, необходимо выявить, на границах каких ограничений находится оптимальная точка. Эти ограничения выполняются как равенства (связанные, или активные, ограничения), остальные – как строгие неравенства (несвязанные, неактивные ограничения). Это важная информация. Для задачи производственного планирования ограничения соответствуют ресурсам. Равенство левой и правой частей ограничения, его активность означает полное использование данного ресурса. Строгое неравенство – неполное использование ресурса.

Знание того, какие ресурсы как используются, определяет узкие места в обеспечении производственного процесса и возможность маневра. Можно, например, продать излишки ресурсов для получения дополнительного дохода. Можно, наоборот, докупить дополнительные объемы тех ресурсов, которые используются полностью. Эти новые объемы вместе с оставшимися излишками других ресурсов позволят выпустить дополнительную продукцию и получить дополнительный доход. Для того чтобы оценить выгодность такого решения, следует оценить величину такого дополнительного дохода, то есть величину предельной эффективности ресурсов. Величина предельной эффективности называется также теневой ценой (или двойственной оценкой) ресурса. Отметим, что теневая цена является внутренней характеристикой ресурса в сложившейся производственной ситуации и не отражает ценность данного ресурса во внешней среде, его рыночную цену. Теневая цена определяет оценку чувствительности оптимума к изменению правых частей ограничений. Сопоставление теневой и рыночной цены может служить основанием для принятия решения о закупке дополнительных объемов данного ресурса (если теневая цена больше рыночной) или о продаже части ресурса (если теневая цена меньше рыночной). В решениях такого рода важным является вопрос о границах действия теневой цены, а, тем самым, и о разумных объемах купли-продажи ресурса.

Ценовой анализ

Изменение оптимального плана может быть связано с изменением цен на продукцию (коэффициентов при переменных в целевой функции). В рассматриваемой модели цены считаются неизменными. При небольших изменениях цен оптимальный план обычно сохраняет свою оптимальность. При существенных изменениях цен оптимальным становится другой план. Важно разобраться в этом, рассчитать критические ценовые границы. Такое изучение воздействия ценовых изменений на оптимальный план и оптимум относят к ценовому постоптимизационному анализу.

( ВЕЗДЕ ОПИСАН ТОЛЬКО ПРИМЕР)

Обратимся к нашему примеру. Цена Печенья составляет 32 руб. за кг. Предположим, что отпускная цена изменилась, и теперь Печенье продается по другой цене. Следует ожидать, что при этом изменится выручка от продаж. Однако изменится ли оптимальный план? Небольшое изменение этой цены приведет к незначительному повороту градиента (вместе со всей системой перпендикулярных ему линий уровня целевой функции). В результате оптимальный план останется в прежней точке (рис. 1.8). При более значительном изменении цены он перейдет в другую вершину области допустимых планов.

Рассмотрим этот вопрос подробнее. Предположим, что цена Печенья увеличивается. Это соответствует повороту градиента по часовой стрелке. Вместе с ним поворачивается и перпендикулярная ему линия уровня (пунктирная линия на рис. 1.8). При небольшом повороте оптимальный план остается в первоначальной точке L. При достаточно большом повороте оптимальный план перейдет в точку M, находящуюся на пересечении границ по Муке и Маслу (линий A1A2 и B1B2). Критическая величина цены, при которой происходит переход оптимального плана из одной точки в другую, соответствует положению, когда линия уровня целевой функции параллельна прямой А1А2 (а градиент, соответственно, перпендикулярен этой прямой). Условием параллельности прямых является пропорциональность коэффициентов при переменных в двух уравнениях: линии уровня целевой функции и границы по Муке. Составим пропорцию с неизвестной ценой c1 первого продукта (Печенья):

С1/0.5 = 27/0.3

Отсюда получаем c1 = 45. Таким образом, при увеличении цены Печенья с первоначальных 32 до 45 руб. за кг (и при сохранении цены Бисквитов) оптимальный план остается неизменным, по-прежнему следует производить 1250 кг Печенья и 666,667 кг Бисквитов. Если же цена поднимется выше 45 руб., то оптимальным планом станет точка M, находящаяся на пересечении границ по Муке и Маслу (линий A1A2 и B1B2). Ее координаты можно определить решением системы уравнений:

0.5x1 + 0.3x2 = 825

0.3x1 + 0.06x2 =480

откуда x1 = 1575, x2 = 125.

При цене Печенья, в точности равной 45 руб., оптимальным является как первоначальный план L, так и новый план M, а также и все точки, лежащие на отрезке LM. В этом случае задача имеет бесконечно много оптимальных планов. Разумеется, все эти разные планы производства обеспечивают в точности одну и ту же величину выручки от продаж. Так, план L соответствует выручке:

451250 + 27666,667 = 74250 (руб.).

План M соответствует той же величине выручки:

451575 + 27125 = 74250 (руб.).

Верхняя критическая граница цены Печенья равна 45. Отсюда следует, что допустимое увеличение первоначальной цены равно 13. Аналогичным образом рассчитывается нижняя граница цены первого продукта. При уменьшении цены Печенья градиент вместе с линиями уровня будет поворачиваться против часовой стрелки. При достаточно сильном повороте оптимальный план перейдет в точку K с координатами

x1 = 818,182, x2 = 954,545.

Критическое положение определяется из условия параллельности линии уровня целевой функции и линии Сахара D1D2. Составим пропорцию:

С1/0.2 = 27/0.3

решив которую получим c1 = 18. Мы получили нижнюю критическую границу цены Печенья, равную 18 руб. Допустимое уменьшение первоначальной цены Печенья, равной 32 руб., составляет 14 руб.Таким образом, при произвольных изменениях цены Печенья между нижней и верхней критическими границами, то есть между 18 и 45 руб., оптимальный план остается прежним: по-прежнему следует производить 1250 кг Печенья и 666,667 кг Бисквитов. При выходе цены за верхнюю или нижнюю критические границы оптимальный план изменится, вместе с ним изменится и статус ресурсов. Аналогичным образом вычисляются нижняя и верхняя границы по

второму продукту – Бисквитам. Отметим, что изменение цены по разным продуктам по-разному воздействует на направление поворота градиента. При увеличении цены второго продукта градиент поворачивается против часовой стрелки, а при уменьшении – по часовой стрелке. Расчеты показывают, что верхняя критическая граница цены Бисквитов равна 48 руб., так что допустимое увеличение составляет 21 руб. При преодолении этой границы оптимальный план переходит из точки L в точку K. Нижняя критическая граница цены Бисквитов равна 19,20 руб., допустимое уменьшение составляет 7,80 руб. При переходе через эту границу оптимальный план переходит из точки L в точку M. Критические границы цен соответствуют границам устойчивости оптимального плана при изменении коэффициентов целевой функции

.