Міністерство освіти і науки України

Одеська державна академія будівництва та архітектури

Кафедра опору матеріалів

Методичні вказівки

“Геометричні характеристики плоских перерізів

в прикладах та задачах”

для усіх спеціальностей

Одеса-2009

"ЗАТВЕРДЖЕНО"

Вченою Радою

інженерно-будівельного

інституту ОДАБА

Укладачі:

доцент, к.т.н. Кушнарьова Г.О.

доцент, к.т.н. Ковров А.В.

асп. Синюкіна Т.А.

"Геометричні характеристики плоских перерізiв в прикладах та задачах". Наводяться теоретичні вiдомостi по геометрії перерiзiв, приклади по визначенню моментів iнерцiї складних перерiзiв, а також розглянуто використання геометричних характеристик в основних задачах опору матерiалiв при розрахунках стержнів на мiцнiсть, жорсткість та стiйкiсть.

Рецензенти:

завідуючий кафедрою металевих,

дерев’яних i пластмасових

конструкцій ОДАБА,

д.т.н., проф. Стоянов В.В.

завiдуючий кафедрою теоретичної

та прикладної механіки ОНМУ,

д.т.н., проф. Гришин В.О.

професор кафедри динаміки,

міцності машин та опору матеріалів

д.т.н. Оробєй В.Ф.

Вiдповiдальний за видання:

Завідувач кафедри опору матерiалiв ОДАБА к.т.н., проф. Карпюк В.М.

Розділ 1. Короткі теоретичні дані

Вступ.

Несуча властивість та жорсткість елементів конструкції визначаються розмірами поперечних перерiзiв i суттєво залежать вiд їх форми.

Площа поперечного перерізу стержня являється мірою затрати матеріалу, але не являється мірою надiйностi. Так при однакових площах поперечних перерiзiв стержень "б" має більший запас стiйкостi, ніж балка"а" (рис.1). Балка "а" являється більш міцною та жорсткою, ніж балка "б" (рис 2.).

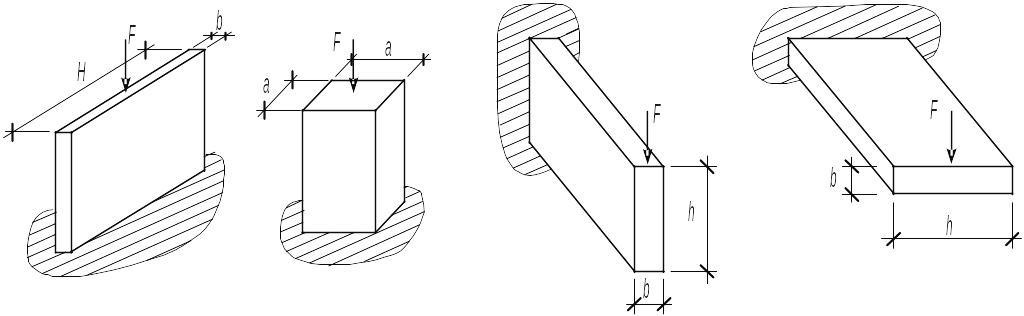
Рис.1 Рис. 2

Ці особливості ураховуються в формулах опору матерiалiв спеціальними геометричними характеристиками поперечних перерiзiв стержнів, які i будуть вивчені в цьому посібнику.

Поперечні перерізи стержнів представляють iз себе плоскі фігури, тому можна говорити про геометричні характеристики плоских фігур.

1.1 Статичнi моменти плоских фiгур.

Теорія статичних моментів стосовно до визначення центрів ваги плоских фігур розглянуто в курсі теоретичної механіки. Тому коротко нагадаємо тільки основні положення.

Статичним моментом елементарної площадки dА відносно осi, яка міститься в її площині (рис.3), називається добуток площі елементарної площадки на координату її до центру ваги:

(1)

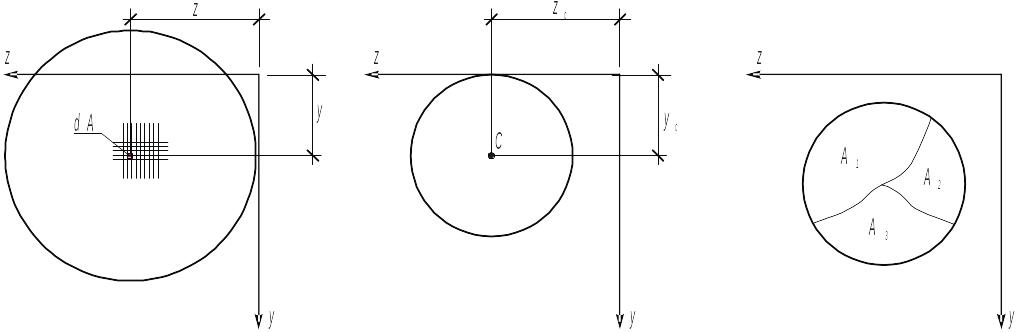
Рис.3 Рис.4 Рис.5

Для того, щоб одержати статичний момент усієї фігури, необхідно скласти статичні моменти елементарних площадок:

(2)

Якщо відомо положення центру ваги фігури (рис 4), то статичні моменти можна визначити так:

(3)

де y_c та z_c - координати центру ваги перерізу

Якщо урахувати властивість інтегралу по площі

або (4)

де

то, використовуючи (3), одержимо формули для визначення координат центру ваги складної фігури.

(5)

Із (3) також випливає, що статичний момент плоскої фігури відносно осi, яка проходить через її центр ваги, рiвен нулю.

Статичний момент має знак, який вiдповiдає знаку координати центру ваги перерізу.

1.2. Осьовi моменти інерції плоских фігур.

Осьові моменти інерції входять в формулу для напружень та прогинів при згинанні балок. Вiд моменту інерції перерізу залежить стiйкiсть стиснутого стержня.

Осьовим моментом інерції елементарної площадки dA плоскої фігури відносно осi, яка лежить в її площині, називається добуток площі елементарної площадки на квадрат вiдстанi від її центру ваги до осi:

(6)

Осьові моменти інерції всій фігури відносно осей z та y одержують в результаті складання моментів інерції елементарних площадок цієї фігури:

(7)

Для осьових моментів інерції має місце властивість інтегралу по площі

(8)

Із означення (6) випливають такi властивості:

1) Осьові моменти інерції вимiрюються в одиницях довжини в четвертій степені (cм⁴; м⁴);

2) Осьові моменти інерції - величини суворо додатні.

Мають мiсце формули, якi зв’язують величини моментів інерції відносно паралельних осей,одна з яких проходить через центр ваги фігури (рис 6):

Рис. 6

(9)

де - моменти iнерцiї відносно центральних осей z₁ та y₁

Дійсно, урахувавши, що

и (10)

Отримуємо

Так як, ось z₁ центральна, то Sz₁ = 0, тоді одержимо (9)

1.3 Полярний момент iнерцiї.

Полярний момент iнерцiї мiститься в формулах для напружень та деформацiй при крутiннi.

Полярним моментом елементарної площадки dA плоскої фiгури вiдносно полюса, який знаходиться в її площинi, називається добуток площi елементарної площадки на квадрат вiдстанi вiд неї до полюсу (рис. 7)

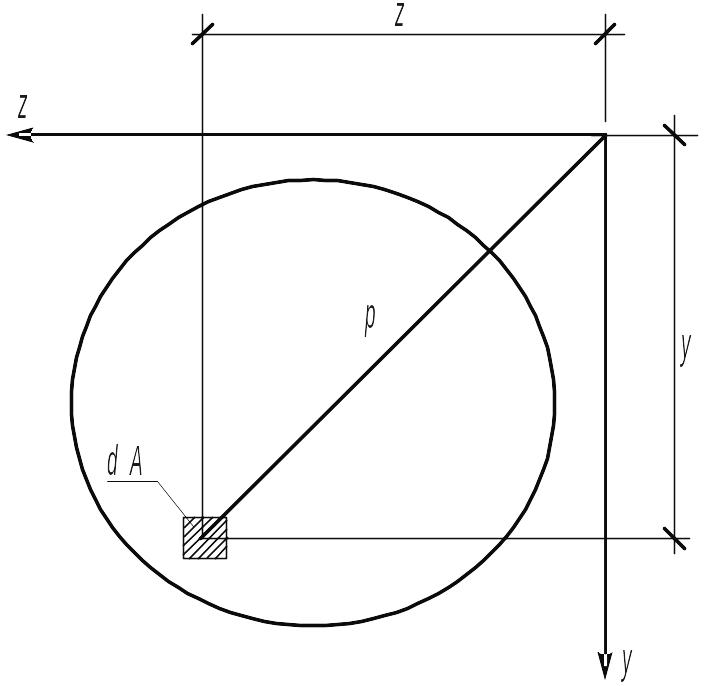
Рис. 7

(11)

тоді

(12)

Якщо за полюс прийняти початок декартової прямокутної системи координат, то із

Випливає

(13)

Таким чином, полярний момент iнерцiї, рівняється сумі осьових моментів iнерцiї відносно двох взаємно перпендикулярних осей, проведених через полюс.

Iз (13) випливає властивість

(14)

Це випливає iз того, що через полюс можна провести скільки завгодно пар взаємно перпендикулярних осей.

1.4 Відцентровий момент інерції

Відцентровий момент iнерцiї не зустрічається в формулах опору матерiалiв завдяки своїй властивості перетворюватися в нуль. В цьому випадку формули приймають найбільш компактний вигляд.

Відцентровим моментом iнерцiї елементарної площадки відносно двох взаємно перпендикулярних осей, які лежать в її площині, називається добуток площі елементарної площадки на її координати:

(15)

Тоді відцентровий момент інерції фігури:

(16)

(17)

Iз визначення (14) випливають такі властивості:

1) відцентровий момент інерції має розмірність (см⁴,м⁴)

2) відцентровий момент iнерцiї, в залежності вiд знаків координат,може бути як додатним, так i від’ємним.

Тому існують осi, відносно яких відцентровий момент iнерцiї рівний нулю. Такі осi називаються головними осями iнерцiї.

Для симетричної фiгури (рис. 8) ось симетрiї являється однією iз головних осей, так як в цьому випадку вiдцентровий момент iнерцiї розбиває фiгуру на дві рiвнi частини, вiдцентровi моменти iнерцiї яких рiвнi по величині, але протилежні по знаку.

Таким чином, для всіх симетричних фігур головні осi установлюють без обчислювань:одна ось співпадає з віссю симетрії, а другу проводять перпендикулярно їй.

В задачах опору матерiалiв важливе значення мають головні вісі, якi проходять через центр ваги перерізу. Такі вісі називаються головними центральними.

На рис.9 показані приклади перерiзiв стержнів, де внаслідок симетрії, положення головних центральних осей очевидно.

Рис. 8 Рис. 9

Має місце формула, яка зв’язує величини моментів інерції відносно паралельних осей , одна пара із яких проходить через центр ваги фігури (рис. 6)

(18)

де –відцентровий момент інерції відносно центральних осей,

y_c та z_c –координати центру ваги фігури в нових осях.

Доведення формули (18) аналогічно приведеному вище для (9). Це рекомендується зробити самостійно.

1.5 Обчислення моментів інерції деяких простих фігур

а) Прямокутник. Обчислимо осьовий момент інерції прямокутника відносно центральної вісі z (рис.10)

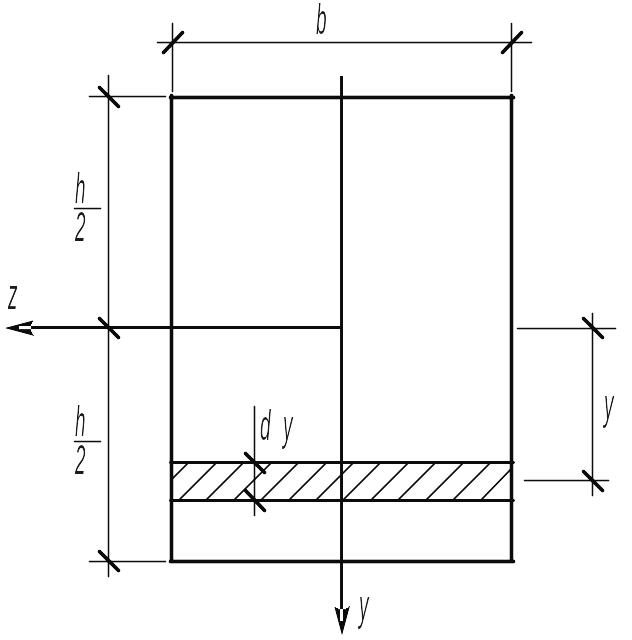
Рис. 10

Згідно до означення необхідно визначити інтеграл (7). Для цього на відстані від осі z виділимо елементарну полоску товщиною dy. Площа її dA = bdy.

Тоді

Аналогічно одержимо формулу . Таким чином:

(19)

б) Паралелограм. Як видно із рис.11, при зміщенні полоси паралельно осі z, її момент інерції відносно останньої не змінюється і, тому усі фігури, одержувані таким зміщенням, мають однаковий момент інерції відносно

осі z.

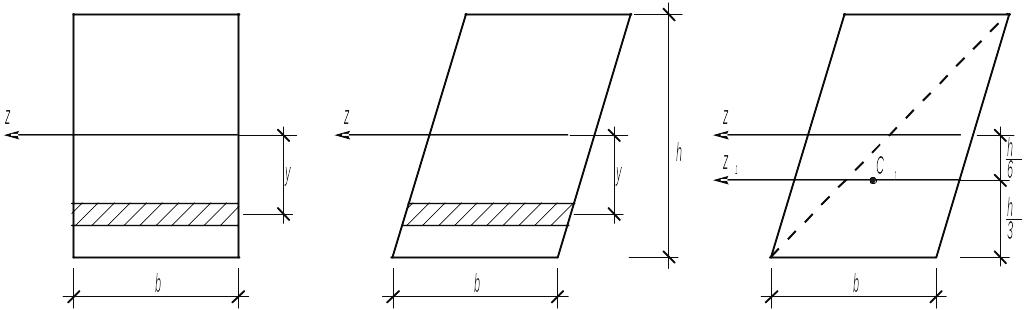
Рис.11

в) Трикутник. Осьовий момент інерції відносно центральної осі, паралельної основі трикутника.

Розбивши паралелограм діагоналлю на два однакових трикутника (рис.12), і використавши формулу (9). Тоді

Урахувавши (19), одержимо рівняння, з якого знайдемо

(20)

Визначення відцентрового моменту інерції прямокутного трикутника.

Проведемо через точку 0, яка лежить на середині гіпотенузи осі z,y, паралельні катетам трикутника.

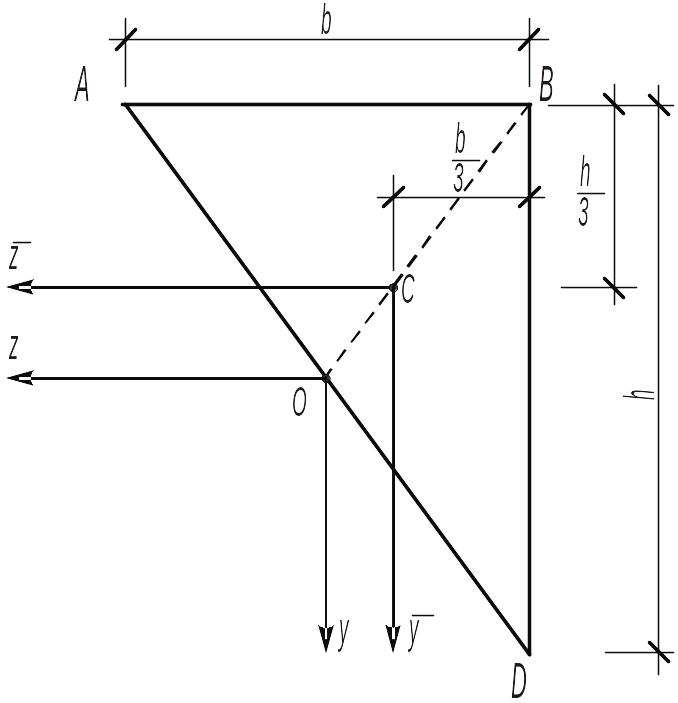
Покажемо, що I_zy =0. Для цього розділимо ▲АВD, лінією ОВ на два трикутника. Для кожного трикутника одна з осей z,y, є віссю симетрії, тому I_zy = 0.

Для визначення відцентрового моменту інерції відносно центральних осей , , скористаємося формулою паралельного переносу (18).

У системі осей z,y, координати центру ваги

Тоді можна записати

Звідси одержимо

(21)

г) Коло. Виділимо у колі (рис 14) елементарну площадку у вигляді кільця товщиною dρ. Її площа Тоді, згідно визначення:

(22)

Ураховуючи, що:

Одержимо: (23)

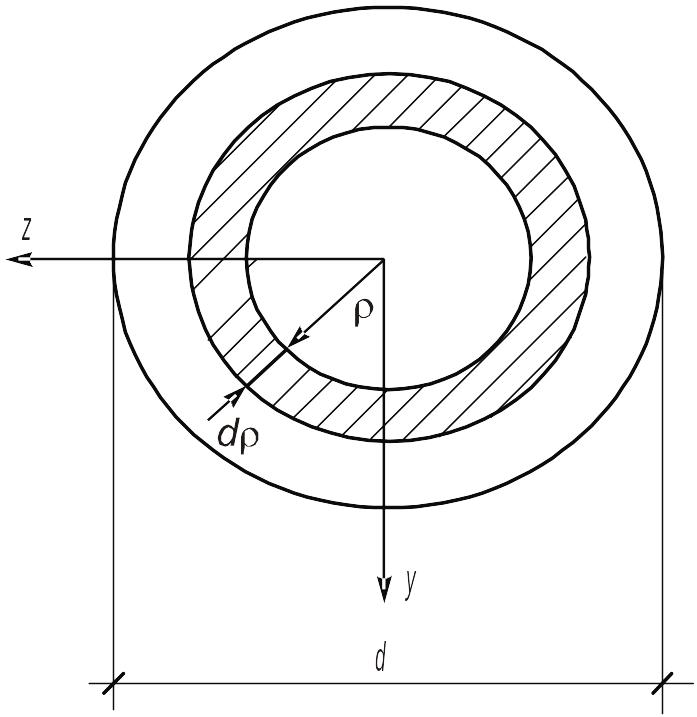
Рис. 14

1.6 Моменти інерції при повороті осей

При повороті координатних осей (рис.15) координати елементарної площадки змінюються так:

(24)

Використовуючи (24), запишемо:

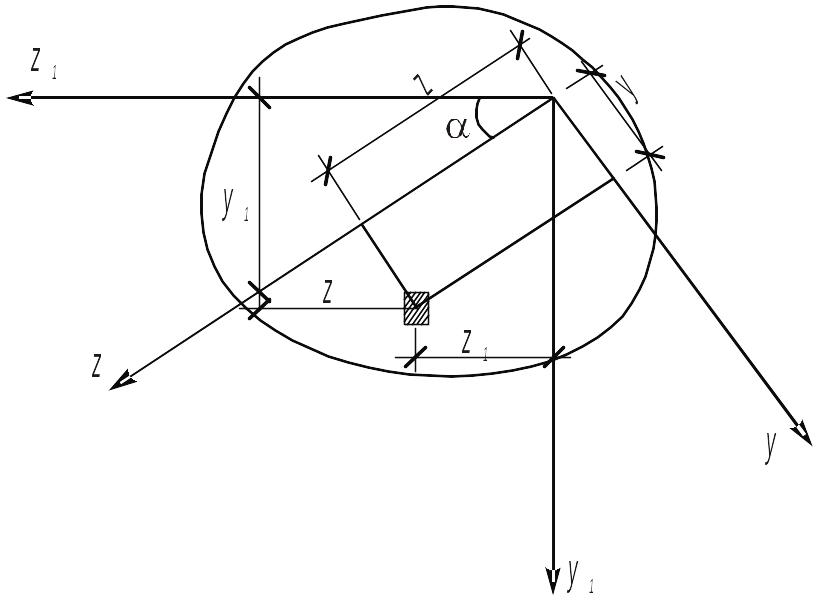
Рис. 15

Аналогічним чином визначимо Iz та Iy. Тоді, враховуючи, що інтеграли, які входять у одержані вирази представляють собою моменти інерції осей Z і Y, одержимо

(25)

(26)

(27)

1.7 Визначення положення головних осей. Головні моменти інерції.

При повороті координатних осей моменти інерції змінюються, підкоряючись залежностям (25),(26). Практичний інтерес представляє запитання про осі, відносно яких осьові моменти інерції приймають екстремальні значення.

Розглядаючи умови екстремальності , одержимо

(28)

Звідси видно,що осьові моменти інерції приймають екстремальні значення відносно осей,для яких , тобто відносно головних осей.

Із властивості (14) виходить, що якщо відносно однієї із головних осей осьовий момент інерції приймає максимальне значення,то відносно другої - мінімальне. Тому(14) можна записати так:

Для визначення розташування головних осей фігури, повернемо вихідну систему (рис.16) на кут , при якому . Тоді, використовуючи (27), маємо:

Звідси одержимо:

(29)

Рис. 16

Аналізуючи одержану формулу, бачимо,що можливі випадки:

(30)

(31)

Розглянемо їх:

1. У випадку (30) рішення (29) має вигляд

Усі ці незлічені рішення визначають положення двох взаємно перпендикулярних головних осей, так як всі рішення при парних значеннях n означають одну ось, а при не парних n- другу, перпендикулярну першій.

2)випадок( 31) буде мати місце при

та

Тут осі , являються головними та головні моменти інерції однакові між собою (не додержується властивість екстремальності).

Визначимо осьові та відцентрові моменти інерції при умовах (33) для довільних осей, повернутих на кут α відносно вихідних головних, використовуючи формули(25)-(27):

(32)

(33)

В цьому випадку виявляється, що всі осі являються головними і моменти інерції цих осей однакові.

Таким чином,показано, що через будь-яку точку фігури, можна провести або одну пару головних осей, або незлічену множину.

Останній випадок має місце для фігур, які мають більш, ніж одну пару головних центральних осей. Такими фігурами є коло та правильний багатокутник (рис17).

Наприклад,

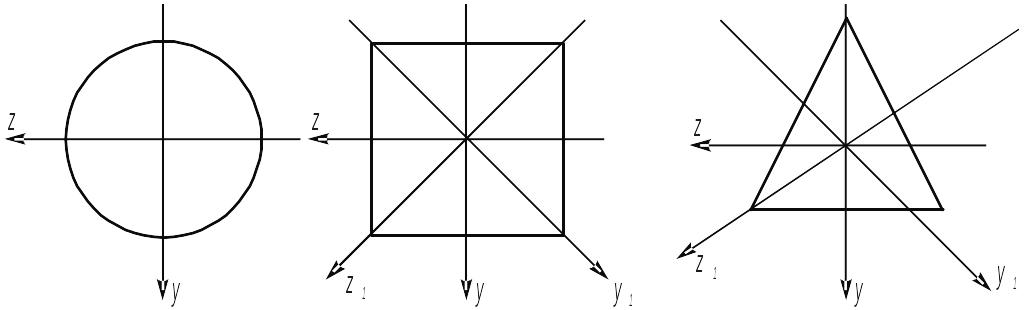
Рис. 17

для квадрата головними центральними осями являються осі симетрії z, y. Крім того, осі z₁ і y₁ - також головні. Теж саме можна сказати і про осі трикутника. Так як головних осей, проведених через дану точку, може існувати або одна пара, або незлічена множина, то ясно, що в розглянутих для квадрата та рівностороннього трикутника,, всі центральні осі є головними.

Величини головних моментів інерції можна визначити по формулам (25), (26), підставивши в них значення кутів α та α₀, визначеного по (29):

(34)

(35)

Виключивши з останніх формул тригонометричні функції кута α₀, і маючи на увазі, що головні моменти інерції екстремальні,одержимо

(36)

Для того,щоб установити, відносно якої з головних осей момент інерції приймає максимальне або мінімальне значення, необхідно порівняти величини I_z та I_y

I_max відноситься до головної осі, розташованої ближче до допоміжної, відносно якої момент інерції більше і навпаки.

Контрольні запитання.

1. Дайте визначення статичного моменту, осьового і відцентрового моментів інерції. Сформулюйте їх властивості.

2. Як визначити положення центру ваги складної фігури?

3. Запишіть залежність між моментами інерції відносно паралельних осей.

4. Запишіть залежності між моментами інерції при повороті координатних осей.

5. Які осі називаються головними? Як визначається їх положення?

6. Як визначити величини головних моментів інерції?

7. Як розв’язати запитання про те, відносно якої з головних центральних осей момент інерції приймає максимальне чи мінімальне значення?

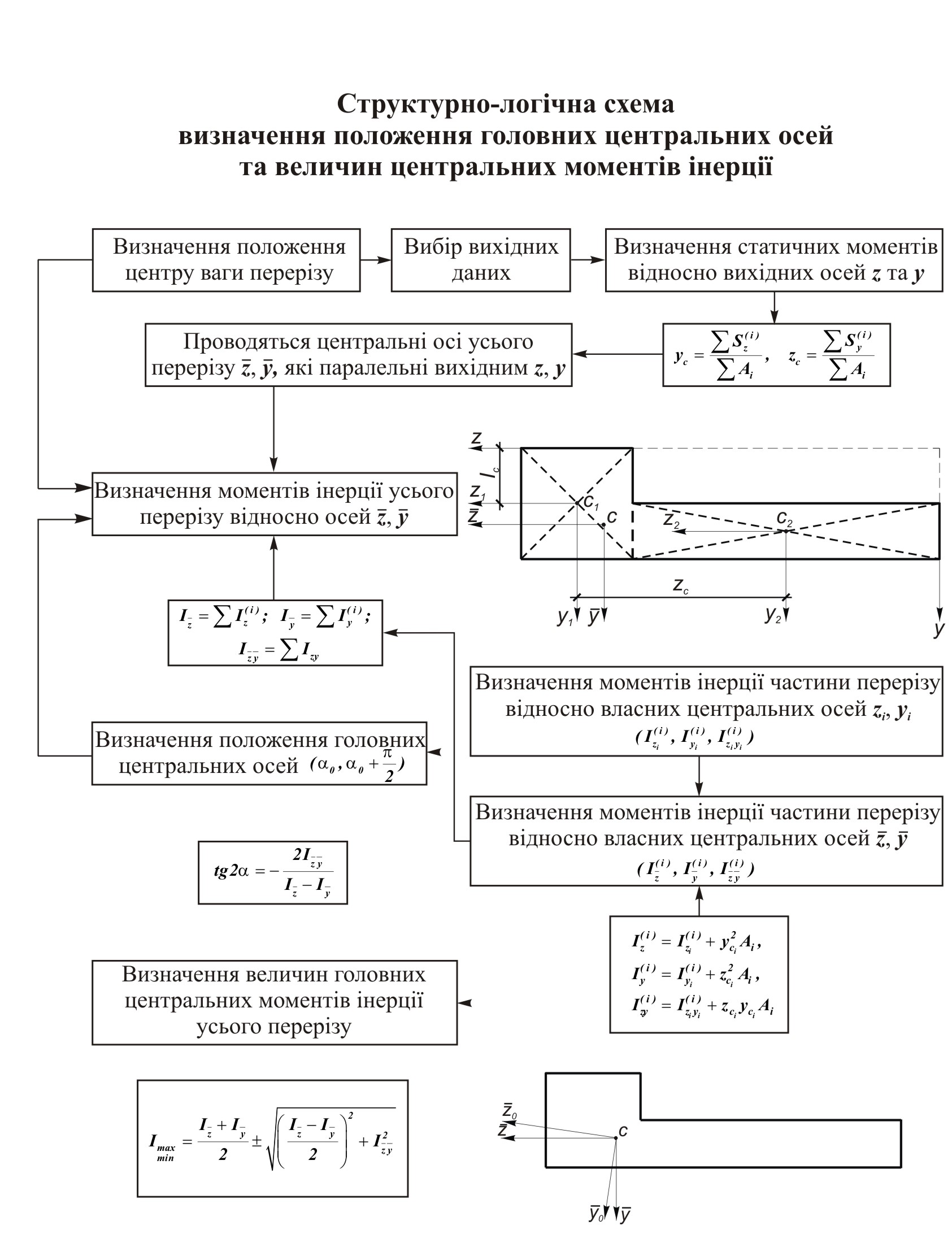
Рис. 18