4.2 Трьохмірна зміна масштабу

Часткова зміна масштабу:

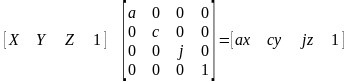(4.3)

Загальна зміна масштабу:

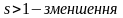
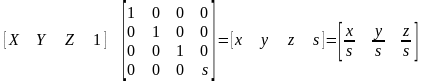(4.4)

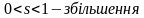
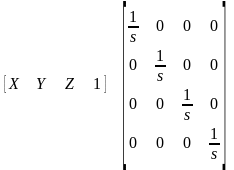(4.5)

4.3 Тривимірний здвиг

Тривимірний здвиг здійснюється наступним чином:

(4.6)

4.4 Тривимірне обертання

Матриці 3х3 забезпечують необхідну операцію зміни масштабу і здвигу, але якщо визначник матриці 3х3 дорівнює 1, то має місце чисте обертання навколо початку координат.

3 Окремих випадки:

1) При обертанні навколо осі x, розміри вздовж осі x не змінюються. Таким чином матриця буде мати нулі в першому рядку і першому стовпчику, за винятком одиниці на головній діагоналі.

Інші елементи визначають при розгляді обертання одиничного куба, вивченими раніше способами. Це приводить до матриці перетворення, відповідної повороту на кут γ відносно осі х.

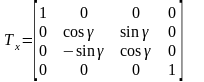(4.7)

2) Для обертання на кут φ, відносно осі y, нулі ставлять у другому рядку і другому стовпчику матриці перетворення, за винятком одиниці на головній діагоналі:

(4.8)

3)

(4.9)

Так як обертання описується множенням матриць, то 3-ох-мірне обертання не комутативне.

4.5 Відображення в просторі

Коли потрібно виконати дзеркальне відображення елемента зображення, то найбільш просто здійснити його відображення відносно площини. Для відображення без зміни масштабів, необхідно щоб визначник перетворення дорівнював .

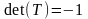При відображенні відносно площини xy, змінюється тільки координата z .

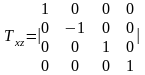
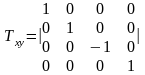
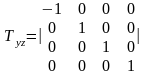(4.10)

4.6 Просторовий перенос

Трьохмірний лінійний перенос визначається перетворенням:

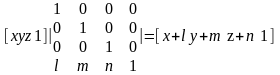
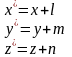(4.11)

4.7 Зображення тривимірних об'єктів

Багато об'єктів, які хотілося б відобразити на дисплеї, є тривимір­ними. Їх машинне зображення з достатньою реалістичністю пов'язане з рядом труднощів:

1) Двовимірна картинка об'єкта в загальному випадку не досить наочна, якщо не ввести в неї інформацію про глибину простору за допомо­гою так званих факторів підвищення наочності глибини;

2) Взагалі важко зображати об'єкти, які містять прямолінійні поверхні, що змушує найчастіше апроксимувати їх багатогранниками. Вже розроб­лено кілька ефективних прийомів побудови зображень тривимірних об'єктів. Будемо називати групу тривимірних об'єктів – просторової сце­ною, а її двовимірне зображення – образом. Об'єкти просторової сцени опи­суються в тривимірній декартовій системі координат, що називається об'єктною ко­ординатною системою. В залежності від точки ,з якої розглядається про­сторова сцена, можна отримати багато образів однієї і тієї ж сцени. Для по­будови конкретного образу необхідно задати точку зору, напрямок спо­стереження і величину кадрового вікна.

Існує кілька способів побудови образів тривимірних сцен. Дуже простий прийом полягає в побудові ортогональних проекцій (план, вид збоку, вид згори, кілька ортогональних проекцій).

Цей прийом заснований на здатності відновлювати просторову сцену (представлену її проекціями). Однак багато хто стикається з трудно­щами при конструкції складних сцен за такими проекціям.

зліва

спереду

зверху

Рис.14 – Ортогональні проекції зображення

Більш придатним є перспективне зображення просторових сцен. Розрізняють такі способи побудови різних видів перспективних проекцій:

• дротових

• контурних

• напівтонових.

Прийоми відрізняються один від одного вимогами до апаратури вивода зображення, обсягами обчислень, необхідними для побудови, і ство­рюваним візуальним ефектом.

1) Дротяні зображення суцільних тіл.

Рис.15 – Дротяні та контурні зображення суцільних тіл

Двовимірний образ являє собою перспективну проекцію сцени з довільної точки. Ефект перспективи дозволяє створити ілюзію глибини зображення. Цей спосіб досить простий і є, ймовірно, єдиним, який можна використовувати в інтерактивних системах без використання спеціальних апаратних засобів.

2) Контурні зображення об'єктів з видаленими невидимими лініями (рис. 15). Образ являє собою перспективну проекцію з довільної (перспективної) точки. Проте лінії або частини ліній закриті поверхнями об'єктів не зображуються. Для реалізації цього способу необхідний значний обсяг обчислень, тим більше що це часто буває не виправданим при побудові оста­точної картини проектованого об'єкта або сцени.

3) Напівтонові зображення об'єктів з видаленими невидимими поверхнями.

Яскравість конкретної поверхні залежить від відбивної здатності і розташування поверхні щодо джерела світла. Для реалізації цього способу потрібний обсяг обчислень набагато більший ніж для попереднього. Однак результатом є побудова масиву точок різної інтенсивності. Подальшим удосконаленням цього способу може бути зобра­ження тіней відображуваних об'єктом.

Рис.16 – Напівтонові зображення об'єктів з видаленими невидимими поверхнями.