3.8 Точки в нескінченності

Використання однорідних координат дає зручний та оперативний спосіб відображення безлічі точок однієї координатної системи в відповідні множини перетвореної системи координат. Як правило нескінченна область однієї координатної системи буде відображатися в кінцеву область іншої координатної системи. При цьому прямі лінії, паралельні в одній системі координат, в загальному випадку, не будуть паралельними в іншій.

Геометричні властивості, наприклад точку перетину, зламу, можна оцінити в будь-якій з цих систем координат.

Нехай дві лінії задані рівняннями

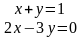
та мають точку перетину

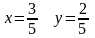
Це рішення може бути отримано в елементарній однорідній системі координат.

Перепишемо рівняння у вигляді

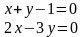
Їх можна представити в матричній формі:

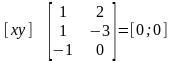
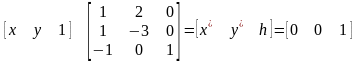
де

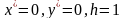
AT=B

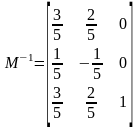
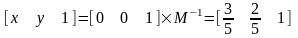
Розглянемо другий тип, який не має зворотної матриці:

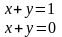
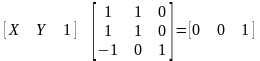
Рішень немає, лінії паралельні tgα=1, але можливий інший вираз, який дозволяє мати зворотну матрицю:

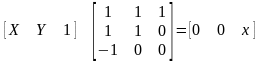
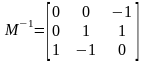
М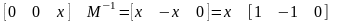 ножимо дві частини рівняння на обернену матрицю.

Результуючі однорідні координати 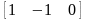повинні представляти “точку перетину” двох паралельних ліній в нескінченності.

Зазвичай двовимірний однорідний вектор [a b 0] утворює точку в нескінченності на лінії ay-bx = 0. Той факт, що вектор з компонентою h=0 представляє точку в нескінченності, може бути продемонстрований наступною процедурою.

Розглянемо лінію 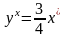та точку .

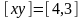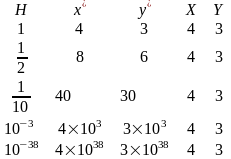
Так як точка може бути представлена в однорідних координатах будь-якими способами, зауважимо, що при H→0 відношення 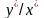залишається рівним 3/4. Далі, наступні, одна за одною пари 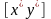, які потрапляють на лінію 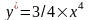стають ближче до нескінченності. Таким чином в межі, коли H → 0, точка прямує до нескінченності [x y H] → [∞ ∞ 1] .

У такій формі однорідні координати дають зручне представлення точки в ∞ в доповнення до властивостей однорідних перетворень.

3.9 Двовимірне обертання навколо довільної осі

Раніше було розглянуто обертання зображення відносно початку координат. Однорідні координати забезпечують поворот зображення навколо точок відмінних від початку координат.

У загальному випадку, обертання навколо довільної точки, може бути виконано шляхом перенесення центру обертання в початок координат, поворотом щодо початку координат, а потім переносом точки обертання у вихідне положення.

Таким чином поворот вектора положення [x y 1] навколо довільної точки M (m, n) на кут θ може бути виконаний так:

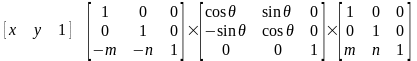(3.18)

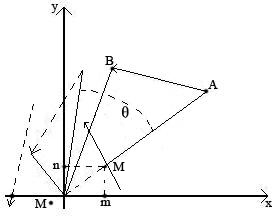
Рис.10 – Поворот вектора навколо довільної точки

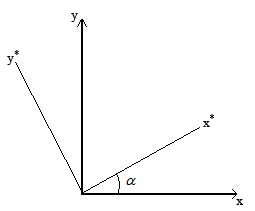
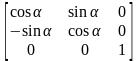
Рис.11 – Обертання навколо осі OZ

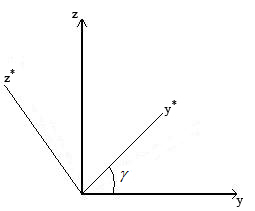
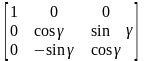
Рис.12 – Обертання навколо осі OX

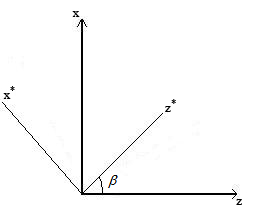
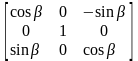
Рис.13 – Обертання навколо осі OY

4. 3D Операції

4.1 Тривимірне перетворення і проекція

Для найкращого сприйняття форми об'єкта, необхідно мати його зображення в трьохмірному просторі. У багатьох випадках початкове уявлення про об'єм, можна отримати лише шляхом виконання операцій обертання і переносу, а також шляхом побудови його проекції. У цьому не важко переконатися на прикладі деякого відносно складного об'єкта. Для того щоб отримати уявлення про його форму, конструктору необхідно виконати операцію обертання та спостереження на деякій відстані з різних сторін і т.д.

Якщо ці операції виконувати за допомогою ЕОМ, то всі результати отримані для плоского зображення, необхідно поширити на просторове. З метою цього введемо знову однорідні координати. Тоді точка в 3-ох-мірному просторі буде представлена в однорідних координатах [x y z] →

[x y z 1] або [X Y Z H].

Перетворення з однорідних координат описується співвідношенням:

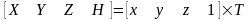( 4.1)

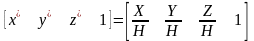
Матриця T – деяка матриця перетворення. Узагальнена матриця перетворень 4х4 має вигляд:

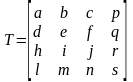
(4.2)

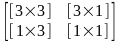
Матриця [3х3] здійснює лінійне перетворення у вигляді: зміни масштабу, здвигу, обертання, відображення. Матриця-стовпець [3х1] – перетворення в перспективі. Матриця-рядок [1х3] – перетворення зміщення. Останній скалярний елемент S – повне перетворення масштабу.

Повне перетворення отримуємо шляхом впливу на вектор положення матрицею [4х4] і нормалізацією перетвореного вектора. Таке перетворення будемо називати – білінійним. Воно забезпечує виконання комплексу операцій (здвиг, зміщення, зміна масштабу та інші).