3.6 Довільна матриця обертання розміру 2х2
Загальну матрицю 2х2, яка здійснює обертання фігури відносно початку координат, можна отримати з розгляду обертання одиничного квадрата щодо початку координат.
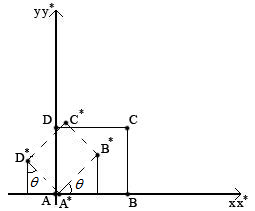
Рис.9 – Обертання одиничного квадрату
Зважаючи на те, що для довільної матриці перетворення розміру 2х2, координати точки визначаються першим рядком матриці перетворень, а координати точки другим рядком, загальна матриця обертання 2х2 має вигляд:
(3.8)
Дане співвідношення відповідає комбінації зміни масштабу і здвигу, яке залишає розміри фігури незміненими. Отже дана матриця перетворення здійснює тільки обертання на довільний кут θ.
3.7 Двовимірне зміщення і однорідні координати
Зміщення
на площині точок і ліній малюнків,
одержуваних з точок і ліній не
обговорювалося. Це обумовлено тим, що
вводити константи перенесення всередину
структури загальної матриці розміру
2х2
не представляється можливим. Але ці
труднощі можна усунути за рахунок
введення 3-ої координати в вектори точок
.
Тобто
представляючи їх у виді:
Матриця перетворення стає матрицею розміру 3х2:
(3.9)
Це необхідно оскільки число стовпців в матриці зображення T = 3, отже в матриці перетворення добавлено 3-ій рядок.
(3.10)
Таким чином:
Звідси випливає що константи m, n викликають зміщення відносно x,y.
Оскільки матриця 3х2 не є квадратною, вона не має зворотної. Цю трудність легко можна подолати, додавши третій стовпець.
(3.11)
Третя компонента векторів положення точок не змінюється при додаванні третього стовпця до матриці перетворення. Додавання третього елементу до вектору положення (1) і третього стовпця до матриці перетворення, дозволяє виконувати зміщення вектора стану.
Третій
елемент тут можна розглядати як додаткову
координату вектора стану. Вектор
положення
при впливі на нього матриці 3х3
стає вектором в загальному випадку виду
.
Задане перетворення було виконано так що:
Перетворення, що має місце в трьохмірному просторі, в нашому випадку обмежено площиною H=1, але якщо третій стовпець (p, q, s) матриці перетворень T, розміру 3х3 відмінний від стовпця (0,0,1), то в результаті матричного перетворення отримаємо:
де H≠1.
Площина, в якій тепер лежить перетворений вектор, знаходиться в трьохмірному просторі.
(3.12)
Представлення двовимірного вектора в трьохмірному, або n-мірного в n+1-мірному, називають однорідним координатним відтворенням.
При однорідному координатному відтворенні n-мірного вектора перетворення виконується в n+1 мірному просторі і кінцевим результатом в n-мірному просторі, отриманому за допомогою зворотного перетворення. Таким чином двомірний вектор [x,y] представлений в однорідних координатах трьохмірним: [xh yh h].
Розділивши на однорідну компоненту, отримаємо перетворений вектор:
(3.13)
Не існує єдиного однорідного координатного представлення точки в двовимірному просторі.
(3.14)
Для простоти обчислень вибираємо [x y 1], щоб представити не перетворену точку в двомірних однорідних координатах.
Перетворення відповідне початковому перетворенню :
(3.15)
Початкове перетворення в однорідних координатах відповідає перетворенню:
(3.16)
Геометрично всі перетворення x і y відбуваються в площині H=1 після нормалізації однорідних координат.
Перевага введення однорідних координат проявляється при використанні матриці перетворення загального вигляду 3х3:
(3.17)
ab, cd – здійснює зміну масштабу, здвиг, відображення, обертання.
m, n – здійснює зміщення.
p, q – отримання проекції.
S – здійснює повну зміну масштабу. Якщо S > 1 – зменшення масштабу, 0 < S < 1 – збільшення масштабу .