2.4 Перетворення прямих ліній
Визначальними є координати двох точок лінії. Вибір типу операцій проведення лінії між точками, буде залежати від типу вихідного графічного пристрою. Розглядати будемо тільки математичні операції з вектором положення. Проведемо пряму лінію на площині, між двома точками A і B з заданими векторами відповідно і вкажемо матрицю перетворення загального вигляду, за допомогою якої відбувається перетворення.
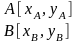
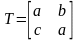
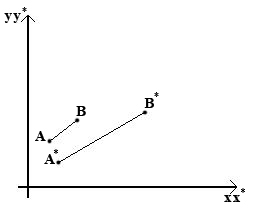
Рис.5 – Зображення ліній AB, A*B*
Використовуючи множення вектора:
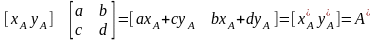(2.12)
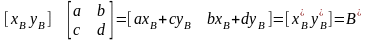
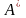– це
нове положення точки A.
–
нове
положення точки B.
Таким чином елементами точок A, B будуть нові координати.
Більш компактно лінія AB може бути представлена у вигляді матриці:
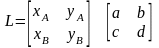
Після множення матриці L на матрицю перетворень T, отримаємо:
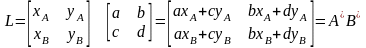(2.13)
2.5 Перетворення середини відрізка
Нехай дано відрізок AB.
Матриця
зображення
.
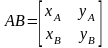Розглянемо середню точку лінії AB:
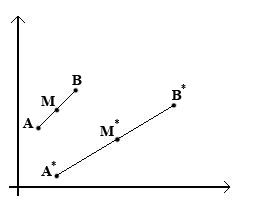
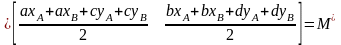(2.14)
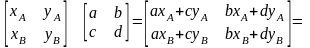
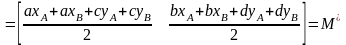(2.15)
Однозначно будь-яке перетворення переводить точку початкового зображення в точку на перетвореному. Перетворення переводить середню точку в середню точку.
Перетворення справедливо для будь-якої вихідної лінії і всі точки на ній перетворюються в точки на іншій лінії. Крім того забезпечується взаємопов'язана відповідність між точками на вихідній лінії і точками на перетвореній лінії.
При застосуванні машинної графіки це означає що положення будь-якої прямої лінії, може бути перетворене в будь-яке нове положення простим перетворенням її граничних точок і наступним проведенням лінії між перетвореними точками.
2.6 Паралельні лінії
Коли матриця 2х2 використовується для перетворення однієї пари паралельних ліній, результатом виявляється інша пара паралельних ліній.
Розглянемо пряму лінію між точками AB і паралельну їй лінію між точками EF:
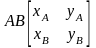
П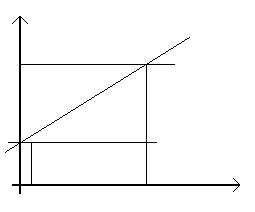
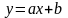
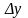
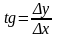
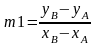окажемо,
що будь-яке однотипне перетворення цих
ліній є також паралельним. Для цього
розглянемо лінії: AB,
EF
і
.
Р
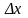ис.6
–
Кут
нахилу прямої
Перетворюючи пряму лінію AB за допомогою загального перетворення 2х2, отримаємо:
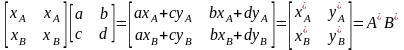(2.16)
Потім визначимо нахил лінії:
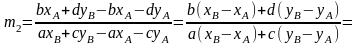
(2.17)
Так
як
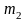не залежить від координат
,
а
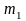,a,b,c,d
мають одні і ті ж значення, як для EF,
так і для AB,
то звідси випливає, що нахил
для
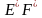дорівнює нахилу для
.
Таким чином паралельні лінії залишаються паралельним після перетворення. Це означає, що паралелограмам перетвориться в паралелограм в результаті дій матриці перетворень 2х2.
3. 2D Операції
3.1 Обертання
Розглянемо плоский трикутник ABC. Цей трикутник повертається на 90° навколо початку координат, проти годинникової стрілки. При цьому здійснюється перетворення між вершинами за допомогою матриці перетворень:
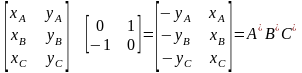(3.1)
Поворот на 180° навколо початку координат:
(3.2)
Поворот на 270° навколо початку координат:
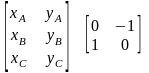(3.3)