Правило нахождения наибольшего и наименьшего значений функции на промежутке [a;b].
Определение1. Говорят, что функция
достигает на множестве X своего наименьшего
(наибольшего) значения в точке
,
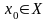если для любого
имеет место неравенство
(
).
Теорема 1. Если функция
непрерывна
на отрезке
,
то она достигает на этом отрезке своих
наименьшего и наибольшего значений.
С
Рисунок 1
ледствие. Если функция дифференцируема на интервале , то она достигает на отрезке наибольшего и наименьшего значений либо в точках экстремума, принадлежащих этому отрезку, либо на концах отрезка.(рисунок 1.)
Для
функции, график которой изображен на
рисунке 1, имеются две точки максимума
(
)
и одна точка минимума (
),
но её наибольшее значение равноf(
,
а наименьшее значение равно f(a).
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке .
1. Найти производную функции
2. Приравнять производную к нулю и найти критические точки функции
3. Отметить критические точки на области определения
4. Вычислить знак производной в каждом из полученных интервалов
5. Выяснить поведение функции в каждом интервале
7. Учитывая поведение функции, определить точки максимума и точки минимума и значения функций в этих точках.
8. Найти значения функции на концах отрезка , то естьнайти f(a) и f(b). После этого, из всех экстремальных значений функции и её значений на концах отрезка выбрать наибольшее и наименьшее.
Пример 1. Исследовать функцию на наибольшее и наименьшее значение на заданном промежутке Х.
Решение:Исследуемая функция дифференцируема и непрерывна на отрезке, поэтому можно применить теорему 1.
а) Найдем производную:
.
б) Найдем стационарные точки (в них производная обращается в нуль).
.
Точки
- точки возможного экстремума. При этом
.
Найдем значения функции в точке
и на концах отрезка и выберем среди них
наибольшее и наименьшее значения. Так
как
,
то
-
наибольшее значение, -
- наименьшее значение функции.
7. Схема исследования функции для построения графика функции.
Найти область определения функции.
Определить возможный тип симметрии функции: чётность или нечётность функции. Функция f(x) называется чётной, если выполнено условие симметрии её графика относительно оси Оу:
f(-x) =f(x).
Функция f(x) называется нечётной, если выполнено условие симметрии её графика относительно начала координат О(0, 0):
f(-x)=-f(x).
При наличии симметрии строится часть графика на правой полуплоскости, а затем она симметрично отображается на левую полуплоскость.
Найти точки пересечения графика функции с осями координат Ох и Оу, т.е. решить соответственно уравнения y = f(0) и f(x) =0.
Найти асимптоты.
Найти точки возможного экстремума.
Найти критические точки.
Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба.
Определить наибольшее и наименьшее значения функции на области её определения.
Построить график функции с учётом проведённого исследования.
Пример 1.Исследовать и построить график функции
Решение:
Область определения функции:
.Функция (5.12) является нечётной, т.к. f(-x) = -f(x).
Уравнение f(x) = 0 даёт корни
.
Пересечения с осью Оу нет в силу
п.1.
4. Имеется вертикальная асимптота –
ось Оу, так как предел f(x)при
бесконечен: при
,
при
.
Определим наклонную асимптоту:
Уравнение наклонной асимптоты: у = х.
5. 
,
т. е. производная нигде не равна нулю и
точек возможного экстремума нет. В
области определения везде
положительна.
6. 
- критических точек нет.
7
.
Функция монотонно возрастает на всей
области своего определения, так как её
производная всюду положительна. В левой
координатной полуплоскости выпуклость
графика функции направлена вниз (
),
в правой полуплоскости выпуклость
направлена вверх (
).
8. Наибольшего и наименьшего значений функции не существует, поскольку область её значений неограниченна.
9. Строим график функции (рис. 5.2).
Практические задания:
1. Исследовать функцию на экстремум, найти точки перегиба, асимптоты и построить график функции y = f(x), если:
а)
б)
2. Зависимость пути от времени при прямолинейном движении задана уравнением S = S(t).
Найти максимальную скорость движения тела и момент времени, когда она будет
достигнута, если:
(м) ;
3. Найти наибольшее и
наименьшее значения функции y
= f(x)
на отрезке
,
если:
