
- •Тема 1: «Определители и матрицы. Системы уравнений с тремя переменными».
- •Правило вычисления определителя второго порядка.
- •Правило вычисления определителя третьего порядка (правило Саррюса)
- •Правило Крамера для решения систем уравнений.
- •2. Система трех линейных уравнений с тремя неизвестными:
- •Тема 2: «Пределы функции».
- •Предел функции в точке (определение). Предел функции в точке.
- •Бесконечно малая функция в точке (на бесконечности).
- •Бесконечно большая функция в точке (на бесконечности).
- •Теоремы о связи между бесконечно малой и бесконечно большой функциями в точке.
- •Теоремы о пределах функции:о сумме; о произведении; о частном двух функции; о постоянном множителе).
- •Правило раскрытия неопределенности типа .
- •Замечательные пределы.
- •Тема 3: «Производная функции».
- •1.Определение производной функции, геометрический и физический смыслы производной.
- •Геометрический смысл производной
- •Физический смысл производной
- •Правила дифференцирования суммы, произведения, частного двух функций:
- •3.Таблица производных элементарных функций.
- •4.Сложная функция и правило ее дифференцирования.
- •Тема 4: «Применение производной функции в построении графиков функции».
- •1. Теорема о признаке возрастания (убывания) функции на промежутке. Правило исследования функции на монотонность.
- •Алгоритм нахождения промежутков возрастания и убывания функции
- •Алгоритм нахождения экстремумов функции
- •Ответ: , .
- •3. Выпуклость и вогнутость кривой на промежутке.Точка перегиба графика функции.
- •Правило исследования функции на выпуклость вогнутость кривой и нахождения точек перегиба графика функции.
- •Асимптоты графика функции: вертикальные, горизонтальные, наклонные.
- •Правило нахождения наибольшего и наименьшего значений функции на промежутке [a;b].
- •Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке .
- •7. Схема исследования функции для построения графика функции.
- •Тема 5: «Неопределённый интеграл».
- •Определение неопределенного интеграла. Понятие первообразной функции
- •Неопределённый интеграл
- •Свойства неопределенного интеграла.
- •Непосредственное интегрирование.
- •Метод подстановки при нахождении неопределенных интегралов.
- •Формула интегрирования по частям.
- •Тема 6: «Определённый интеграл».
- •Определение и площадь криволинейной трапеции.
- •Формула Ньютона-Лейбница. Формула Ньютона-Лейбница это основная формула интегрального исчисления:
- •О бъём тела вращения
- •4. Основные свойства определённого интеграла
- •4. Вычисление определённых интегралов.
- •5. Интегрирование заменой переменной.
- •7. Интегрирование по частям.
- •Основные свойства интегралов.
- •Тема 7: «Комплексные числа».
- •Тема 8: Комбинаторика. Теория вероятностей.
3.Таблица производных элементарных функций.
1.
 где С – постоянное число.
где С – постоянное число.
2.
 ;
в частности,
;
в частности,
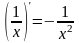 ,
,

3.
 в частности,
в частности,

4.
 в частности,
в частности,

5.
 6.
6.

7.
 8.
8.

4.Сложная функция и правило ее дифференцирования.
Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
 (5)
(5)
Пример 1.
Найти производную функции


Практические задания:
Найти производные функции:
1. 2.
2.

3.
 4.
4.
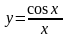
5.
 6.
6.

Тема 4: «Применение производной функции в построении графиков функции».
1. Теорема о признаке возрастания (убывания) функции на промежутке. Правило исследования функции на монотонность.
Некоторые функции во всей своей области определения изменяются монотонно - только возрастают или только убывают. Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают.
Определение 1:Функция называется возрастающей на интервале, если с возрастанием значений аргумента значения функции тоже возрастают.
Определение 2:Функция называется убывающей на интервале, если с возрастанием значений аргумента значения функции убывают.
Возрастание и
убывание функции
 характеризуется знаком ее производной
характеризуется знаком ее производной
 .
.
Теорема:если
в некотором интервале
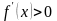 ,
то функция возрастает, а если
,
то функция возрастает, а если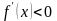 ,
то функция убывает в этом интервале.
,
то функция убывает в этом интервале.
Алгоритм нахождения промежутков возрастания и убывания функции
1. Найти область определения функции
2.Найти производную функции
3. Приравнять производную к нулю и найти критические точки функции
4. Отметить критические точки на области определения
5. Вычислить знак производной в каждом из полученных интервалов
6. Выяснить поведение функции в каждом интервале.
Пример: Найдите промежутки возрастания
и убывания функцииf(x)
=
 и
число нулей данной функции на промежутке
[0; 10].
и
число нулей данной функции на промежутке
[0; 10].
Решение:
D(f) = R
f '(x) =

D(f ') = D(f) = R
Найдём критические точки функции, решив уравнение f'(x) = 0.
x(x – 10) = 0

критические точки функции x = 0 и x = 10.
Определим знак производной.
f'(x) + – +

f(x) 0 10x
в промежутках (-∞; 0) и (10; +∞) производная функции положительна и в точках x = 0 и x = 10 функция f(x) непрерывна, следовательно, данная функция возрастает на промежутках: (-∞; 0]; [10; +∞).
В промежутке (0; 10) производная отрицательная и в точках x = 0 и x = 10 функция f(x) непрерывна, следовательно, данная функция убывает на промежутке [0; 10].
Определим знак значений функции на концах отрезка.
f(0) = 3, f(0) > 0
f(10) =
 ,
f(10) < 0.
,
f(10) < 0.
Так как на отрезке [0; 10] функция убывает и знак значений функции изменяется, то на этом отрезке один нуль функции.
Ответ: функция f(x) возрастает на промежутках: (-∞; 0]; [10; +∞);
функция f(x) убывает на промежутке [0; 10];
на промежутке [0; 10] функция имеет один нуль функции.
2. Точки экстремума функции: точки максимума и точки минимума. Необходимое и достаточное условия существования экстремума функции. Правило исследования функции на экстремум.
Определение 1:Точки, в которых производная равна нулю, называются критическими или стационарными.
Определение 2.
Точка
 называется точкой минимума (максимума)
функции
,
если значение функции в этой точке
меньше (больше) ближайших значений
функии.
называется точкой минимума (максимума)
функции
,
если значение функции в этой точке
меньше (больше) ближайших значений
функии.
Следует иметь в виду, что максимум и минимум в данном случае являются локальными.
На рис. 1. изображены локальные максимумы и минимумы.
М аксимум
и минимум функции объединены общим
названием: экстремум функции.
аксимум
и минимум функции объединены общим
названием: экстремум функции.
Теорема 1.
(необходимый признак существования
экстремума функции). Если дифференцируемая
в точке
функция
имеет в этой точке максимум или минимум,
то ее производная при
обращается в нуль,
 .
.
Теорема 2. (достаточный признак существования экстремума функции). Если непрерывная функция имеет производную во всех точках некоторого интервала, содержащего критическую точку (за исключением может быть самой этой точки), и если производная при переходе аргумента слева направо через критическую точку меняет знак с плюса на минус, то функция в этой точке имеет максимум, а при переходе знака с минуса на плюс – минимум.
