8. Замечательные пределы.

 замечательный предел

Теорема:Предел функции в точке х = 0 существует и равен единице, т.е.

Пример 1.Найти предел функции sin (ax)/bx при х → 0.

Решение: Преобразуем данную дробь так, чтобы в знаменателе был аргумент синуса; только тогда можно будет применить первый замечательный предел, поскольку при х → 0 пределом ах также является нуль:

Пример 2.Найти предел

Решение:Теорему о первом замечательном пределе здесь непосредственно применить нельзя, так как при х→0 знаменатель дроби стремится к нулю. Для решения задачи необходимо сначала преобразовать данную дробь, а затем уже выполнить предельный переход:

 замечательный предел

Теорема: Предел функции при существует и равен е, т. е. .

Показательная функция вида называется экспонентой, логарифм с основанием e называется натуральным и обозначается символом ln.

Пример 1.Найти .

Решение:Применим замену переменной, полагая 1 / х = у. Тогда при , т. е. имеем

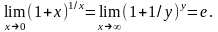
Пример 2.Найти .

Решение:Заменим переменную, положив х = 2у. При последовательно получаем

Практические задания:

Вычислить предел функции:

9. . 10. .

Тема 3: «Производная функции».

1.Определение производной функции, геометрический и физический смыслы производной.

Придадим значению аргумента х₀ функции f(x), определённой на промежутке Х, произвольное приращение Δх так, чтобы точка х₀ + Δх также принадлежала Х. Тогда соответствующее приращение функции f(x) составит Δу = f(x + x₀) – f(x₀).

Определение 1. Производной функции f(x) в точке х₀называется предел отношения приращения функции в этой точке к приращению аргумента Δх→ 0 (если этот предел существует).

Для обозначения производной функции применяют символы или

(1)

Геометрический смысл производной

Определение 2. Касательной к графику функции y = f(x) в точке М называется предельное положение секущей MN, когда точка N стремится к точке М по кривой f(x).

Таким образом, если производная функции f(x) в точке х₀ существует, то

. (2)

Производная равна тангенсу угла между касательной к графику функции y = f(x) в точке М(х₀, f(x₀)) и положительным направлением оси (ох)

Физический смысл производной

Производная функции определяет мгновенную скорость функции.

3. Правила дифференцирования суммы, произведения, частного двух функций:

1. Если функции и дифференцируемы в данной точке , то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:

(1)

Пример 1. Найти производную функции

2. Если функции и дифференцируемы в данной точке , то в той же точке дифференцируемо и их произведение. При этом производная произведения находится по следующей формуле:

(2)

Пример 2. Найти производную функции

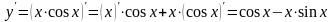
3. Если функция дифференцируема в данной точке , то в той же точке дифференцируема и функция, представляющая собой произведение функции на константу . При этом данную константу можно вынести за знак производной:

(3)

Пример 3. Найти производную функции

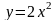
4. Если в данной точке функции и дифференцируемы и , то в той же точке дифференцируемо и их частное , причем:

(4)

Пример 4. Найти производную функции