2.5.Иллюстрации
В тексте любой письменной работы в том или ином количестве обязательно присутствуют иллюстрационные материалы. К ним относятся: графики, диаграммы, схемы, рисунки, фотографии и др. Все они должны иметь расположенную снизу пояснительную подпись, включающую в себя следующие компоненты:
порядковый номер, сквозной (например: рис. 46);
тематический заголовок иллюстрации, выполненный в краткой форме;
расшифровку деталей иллюстрации, обычно обозначаемых на ней буквами или цифрами.
Графики представляют собой компактные и наглядные геометрические изображения функциональных зависимостей в трехмерном или двухмерном пространстве посредством системы координат. В настоящее время практически используются: сферическая, цилиндрическая и линейная (декартова) системы координат.
Последняя из них наиболее распространена. В общем случае она представляет собой три взаимно перпендикулярных луча (координатные оси), исходящих из общей точки, именуемой началом координат.
Традиционно оси координат обозначаются латинскими буквами X, Y, Z, а начало координат – цифрой «0». В такой системе координат (см. рис. 1) графическое изображение функции двух переменных Z = f (x,y), где x и y – аргументы функции, представляет собой криволинейную поверхность (заштрихована на рис. 1). Высота каждой точки на этой поверхности (например, точки Р) по отношению к плоскости X0Y (отрезок РР') определяет значение функции Z. Аргументы X и Y, соответствующие данному значению функции, определяются длиной отрезков nР' и mР' в плоскости X0Y перпендикулярных соответственно осям 0Y и 0X.
На практике чаще встречается потребность графического изображения функции одного переменного Z = f(X). В этом случае достаточно плоской системы координат, на которой данная функция изображается в виде криволинейной линии на плоскости Z0X (см. рис. 2). Каждая точка на этой кривой (например, точка Р) определяет значение функции (отрезок «0n» на оси 0Z) и соответствующее ему значение аргумента функции (отрезок «0m» на оси 0X).
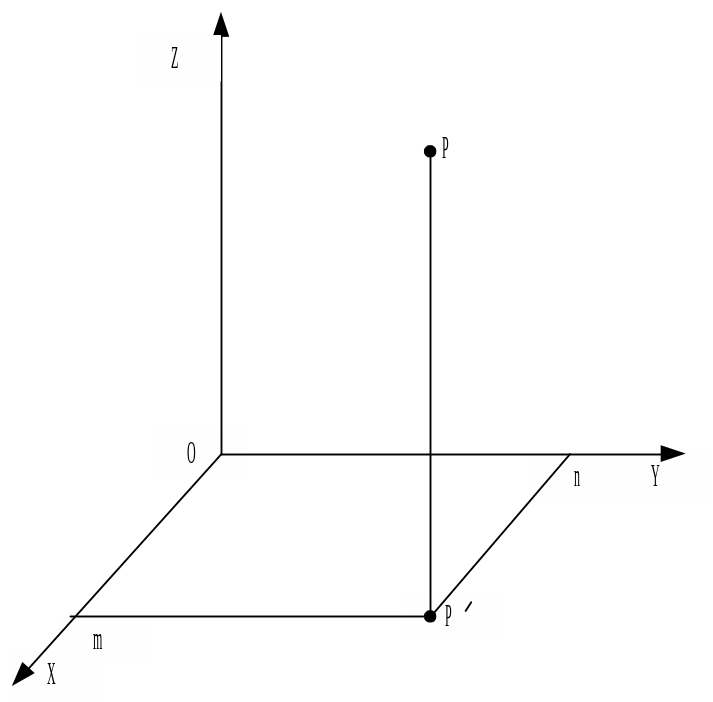
Рис. 1. Изображение функции двух переменных
В трехмерной системе координат.
Рис. 2. Изображение функции одной переменной в двухмерной системе координат: ОХ – ось абсцисс; ОZ – ось ординат.
Важнейшим предварительным условием грамотного построения графика функции является правильный выбор масштабов величин по осям координат. Иными словами, оси координат предварительно должны быть отградуированы. При выборе масштабов следует придерживаться следующих правил.
Масштабные интервалы должны соответствовать целым числам (см. рис. 3).
Рис. 3. К вопросу о правильном выборе масштаба.
Одинаковые масштабные интервалы должны иметь одинаковую линейную протяженность.
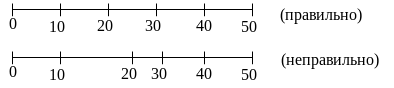
Рис. 4. К вопросу о правильном выборе масштаба.
Числовые значения масштабных шкал на осях координат пишутся за пределами поля графика (левее от оси ординат, ниже оси абсцисс). Сами оси координат должны быть обозначены сплошными линиями и без стрелок на концах. На осях координат должны быть указаны условные обозначения и размерности отложенных величин (например: V, м/с).
Пояснительных надписей на графиках обычно не пишут. Их заменяют цифрами, которые расшифровываются в подрисуночной надписи.
Выносить вспомогательные цифры и надписи на оси координат без крайней надобности не следует.
В случаях, когда с графика необходимо снимать точные числовые данные, координатное поле размечают масштабной сеткой.
Таким образом, грамотно выполненный график функции должен иметь следующий вид (см. рис. 5а, б).
На графиках, носящих иллюстративный характер (без указания масштабов), на осях координат наносятся стрелки, указывающие направление возрастания соответствующих параметров.
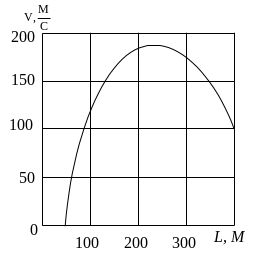
Диаграмма – один из способов графического изображения зависимости между величинами. Она составляется для наглядного и компактного изображения и анализа массовых данных. В практике наибольшее распространение получили два типа диаграмм: линейные и секторные.