17.Көп айнымалы функциялардың шегі.Қайталама шектер.Функцияның үзіліссіздігі.

Анықтама A саны z = f (x, y) функциясының ( ) нүктесіндегі шегі деп

аталады, егер әрбір ε > 0 үшін uδ( ) аймағындағы барлық (x, y) үшін, осы нүктеден басқа, төмендегі теңсіздік

f (x, y) − A < ε

орындалатындай δ > 0 саны табылса.

Егер z = f (x, y) функциясының ( ) нүктесіндегі шегі A болса, онда ол мына

түрде белгіленеді:

Бір айнымалы функциялар үшін қарастырылған барлық қасиеттер көп айнымалы

функциялар үшін де дұрыс болады.

Анықтама z = f (x, y) функциясы ( ) нүктесінде үзіліссіз деп аталады, егер

төменгі үш шарт орындалса:

1)

бар болса,

2) ( ) нүктесінде функцияның мәні бар,

3)

Функцияның үзіліссіздігін келесі теореманың көмегімен зерттеуге болады.

Теорема Кез келген z = f (x, y) элементар функция өзінің анықталу облысының

барлық ішкі нүктелерінде (шеткі нүктелерінде емес) үзіліссіз болады.

Мысал z = 1− − .

Функциясының үзіліссіз болатын барлық нүктелерін табайық.

Бұрын айтқандай, бұл функция жабық

+ ≤ 1 . дөңгелекте анықталған. Бұл дөнгелектің ішкі нүктелері функцияның ізделінді үзіліссіздік нүктелері, немесе z = 1− − функциясы ашық + < 1 дөнгелекте үзіліссіз.

18.Дербес өсімшелер мен дербес туындылар.Күрделі функция туындысы.

Анықтама z = f (x, y) функциясының ( ) нүктесіндегі x бойынша өсімшесі

Δx -ке сәйкес x бойынша дербес өсімшесі деп айтамыз:

Δ x f = f ( + Δx, y0 )− f ( ).

Бұл өсімше, бір айнымалы z = f (x, ) функцияның y = тұрақты болғанда f (x, y)

функциясының өсімшесі болады.

Сол сияқты z = f (x, ) функциясының ( ) нүктесіндегі y - бойынша өсімшесі Δy −ке сәйкес y бойынша дербес өсімшесі деп мына айырманы айтамыз:

Δ y f = f ( , + Δy)− f ( , ) .

Бұл өсімше x = тұрақты мәнінде есептелінеді.

Мысал f (x, y) = xy, = 3, = 4, Δx = Δy = 0,1 болсын.

x, y бойынша функцияның дербес өсімшелерін табайық:

Δ x f = (x + Δx) − = + Δ − = Δx = 4⋅0,1 = 0,4 ;

Δ y f = ( + Δy)− = + Δy − = Δx = 3⋅0,1 = 0,3 ;

Бұл мысалда аргументтердің бірдей өсімшелерінде Δx,Δy , дербес өсімшелер әртүрлі.

Бұл тікбұрыштың қабырғалары = 3, = 4 болатын, -ді Δx = 0,1 ге өсіргенде ауданының

Δ x f = 0,4 -ке, ал қабырғасын Δy = 0, 1-ге өсіргенде ауданының Δ y f = 0,3 - ке өсетінін

білдіреді. (2 сур. қара).

Анықтама z = f (x, y) функциясының ( ) нүктесіндегі дербес

туындысы деп осы функцияның x бойынша дербес өсімшесінің, осы нүктедегі, x

аргументінің өсімшесі Δx - ке қатынасын айтады:

Мұндай дербес туындылар ,

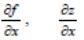символдарымен белгіленеді. Соңғы

жағдайда ∂ -әрпі «дербес» сөзін береді.

Осы ( ) нүктесіндегі y бойынша дербес туынды мына

шекпен анықталады.

Бұл дербес туындының басқа белгіленулері:

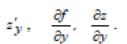
Функциялардың дербес туындысы бір айнымалы функцияның туындыларын табу ережелері бойынша табылады, дифференциалданатын айнымалыдан басқа айнымалалар тұрақты деп есептелінеді.

− табу кезінде y турақты деп есептеледі, ал тапқанда x - тұрақты деп eсептеледі

Анықтама z = f (u,v) , u = u(x, y), v = v(x, y) функцияларынан құрылған

күрделі функция деп екі (x, y) айнымалыларынан тұратын z = f (u(x, y),ν (x, y))

функцияны айтамыз.

2 теорема u = u(x, y),және v = v(x, y) функцияларының x бойынша ( )

нүктесінде x , y бойынша дербес туындылары болсын, ал z = f (u,ν ) функциясы және

оның u мен ν бойынша дербес туындылары нүктесінің маңайында үзіліссіз болсын, = u( ), =ν ( ) Онда күрделі функцияның

z = f (u(x, y),ν (x, y)) (4)

( ) нүктесінде дербес туындылары бар және мына формулалармен табылады:

.