Формула степенной простой в общем виде

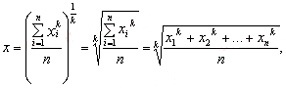
где:

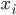— индивидуальное значение признака -й единицы совокупности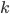
— показатель степени средней величины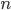
— число единиц совокупности

Формула степенной средней взвещенной в общем виде

где:

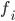— частота повторения -й варианты.

В зависимости от того, какое значение принимает показатель степени средней величины , получаем различные виды средних:

При расчете различных степенных средних по одним и тем же данным значения средних будут неодинаковыми. Чем выше показатель степени ( ), тем больше величина средней, т.е. действует правило мажорантности средних:

28. Способы расчета дисперсий

29. Понятие индекса сезонности и способы их расчета

Сезонными колебаниями называют внутригодичные, постоянно повторяющиеся изменения изучаемых явлений. При анализе рядов внутригодовой динамики получают количественные характеристики, отражающие характер изменения показателей по месяцам годового цикла. Сезонные колебания описывают индексами сезонности, которые рассчитываются как отношение фактического значения показателя к некоторому теоретическому (расчетному) уровню Где i - порядковый номер сезонного цикла (года), j - порядковый номер внутрисезонного периода (месяца) Полученые значения подвержены случайным отклонениям, поэтому производится усреднение по годам и получение средних индексов сезонности для каждого периода годового цикла (месяца) В зависимости от характера изменений ряда динамики формула может рассчитываться разными методами.

30. Виды коэффициентов корреляций и их применение

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой. Линейный коэффициент корреляции

Для устранения недостатка ковариации был введён линейный коэффициент корреляции, который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон . Коэффициент корреляции рассчитывается по формуле:

где , — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где — коэффициент регрессии, — среднеквадратическое отклонение соответствующего факторного признака^[12]. Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).

Коэффициент ранговой корреляции Кендалла Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла: