1. Жиын және оның элементтері. Ішкі жиын.

Желілік модельдердің теориялық негізі - жиындар мен графтар теорияларына негізделеді. Математикада XIX ғасырдың екінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Георг Кантор (1845-1918) болды.

Белгілі бір ортақ қасиеттерге ие болып, белгілі бір заңдылықпен біріккен нәрселер, объектілер жиын құрайды.

Жиындар элементтерден құралады. Жиындардың элементтері аталып беріледі немесе сол жиын элементтеріне ғана тән қасиет (белгі) көрсетіледі. Жиынды латынның бас әрпімен белгілеп, оның элементтерін фигуралық жақшаның ішіне алып жазу келісілген. Мысалы, “планета» сөзіндегі әріптер жиынын P әрпімен белгілесек, P={а,п,н,л,е,т} немесе P={т,п,н,л,е,а} элементтер ретін әр-түрлі жазуға болады.

Жиындар шектеулі жиын, шектеусіз жиын болып бөлінеді. Мысалы, цифрлар жиыны A – шектеулі жиын, оған 10 элемент енеді. A={0,1,2,3,4,5,6,7,8,9} жиынының элементтер санын көрсетіп жазсақ: n(A)=10. Ал натурал сандар жиыны N ={1,2,3,4,…} - шектеусіз жиын.

Егер a элементі B жиынына тиісті болса, оның жазылуы: a ∈ B. Оқылуы: «a B жиынының элементі» немесе «a B жиынына тиісті».

Мысалы, 7 саны натурал сандар жиынына тиісті: 7 ∈ N.

Егер c элементі A жиынына тиісті болмаса, оның жазылуы: c ∉ A. Оқылуы: « c A жиынына тиісті емес». Мысалы, 0 саны натурал сандар жиынына тиісті емес:

0 ∈ N.

Егер жиында бірде-бір элемент болмаса, оны бос жиын деп атайды. Бос жиынның белгіленуі: Ø. Мысалы, 74 және 79 сандарының арасындағы жай сандар жиыны - бос жиын.

Егер B жиынының әрбір элементі A жиынына тиісті болса, онда B жиыны A жиынының ішкі жиыны деп аталады. Мысалы, A={1,2,3,4,5,6,7} жиынындағы жұп сандар жиыны – B={2,4,6}. B жиынының әрбір элементі A жиынына тиісті.

2.Жиындардың қиылысуы

Қандай да бір элементтер тобын жиын деп түсінетінбіз. Мысалы, жазықтықтағы фигуралар (төртбұрыш, шеңбер, ромб, квадрат) жиыны.Жиындарға қиылысу амалын қолдануға болады:

жиындардың қиылысуы (c=a  b). C жиынының әрбір элементі бірмезгілде a мен b жиынының элементі болады.

A жиынына да, B жиынына да тиісті элементтерден ғана тұратын жиынды A және B жиынының қиылысуы деп атайды.

3.Жиындардың бірігуі Қандай да бір элементтер тобын жиын деп түсінетінбіз. Мысалы, жазықтықтағы фигуралар (төртбұрыш, шеңбер, ромб, квадрат) жиыны.Жиындарға бірігу амалын қолдануға болады:

жиындарды біріктіру (c=a  b). C жиынының әрбір элементіне a жиынының элементі, не b жиынының элементі болады.

4.Графтар теориясы

Графтар теориясы (ағылш graph theory) — түйіндері нүктелер жиыны, ал түйіндердің жалғасуы (қабырға деп аталатын) парлы екі нүкте болып келетін тор түрінде бейнеленеді. Кез келген V жиыны мен V жиынының элементтерінің парларынан тұратын Е бинарлық қатынасын граф деп айтамыз. Белгілеуі: G = (V, Е). Егер Е жиынының элементтерін реттелмеген парлар ретінде қарастырсақ, ондай графты багытталмаган деп, ал парлар оның қырлары деп аталады. Кері жағдайда граф багытталган, ал Е жиынының элементтері графтың догалары деп аталады.

(а, а) пар тұзақ делінеді ,егер Е жиынтығында (а, b) пары бірнеше рет кездессе, оны еселі қыр(дога) деп айтады.

Бұдан былай тұзақсыз және еселі қырларсыз графты бағытталмаған(немесе жайғана граф), тұзақсыз графты мультиграф, ал тұзақтар кездесетін мультиграфты псевдограф дейміз.

Қыр арқылы жалғасқан граф төбелерін іргелес деп айтады.

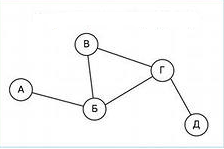
G = (V,Е) графының төбелері мен қырларынан тұратын 0,(0,1), 1,(1,2), 2,…,n-1,(n-1,n),n тізбегін жол деп атаймыз (АБГД, АБВГД). Осындағы n саны жолдың ұзындығы деп аталады. Қырлары қайталанбайтын жолды тізбек деп атайды (АБГД, АБВГД). Төбелері қайталанбайтын жол қарапайым тізбек деп аталады (АБГД, АБВГД).

БВГБ- тұйық жол. Төбелері қайталанбайтын тұйық жол қарапайым цикл деп аталады.

Кез келген екі төбесінің арасында жол болатын графты байланган деп атайды. Әрбір төбе өзімен жол арқылы жалғанған деп есептеледі. Ол жолдың ұзындығы нөлге тең.

 төбесінен төбесіне жол болса, оны i→i, қатынасымен белгілейміз. Бұл қатынас

симметриялы, өйткені i→i i→i,

транзитивті, өйткені (i→i) & (i→k) i→k,

рефлексивті, өйткені і(i→i) .