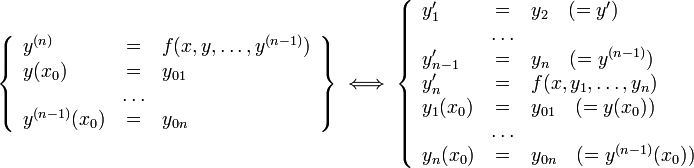46. Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где   — многочлен  -ой степени.

47 Несобственный интеграл

Материал из Википедии — свободной энциклопедии

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

• Абсолютная сходимость

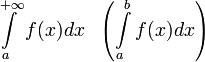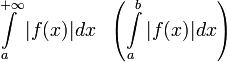• Интеграл   называется абсолютно сходящимся, если  сходится. Если интеграл сходится абсолютно, то он сходится.

• [Править]Условная сходимость

• Интеграл 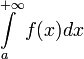  называется условно сходящимся, если   сходится, а 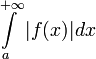  расходится.

• Пример 3

• Вычислить несобственный интеграл или установить его расходимость.

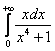
• Подынтегральная функция непрерывна на  .

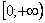• Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.

• Сначала попытаемся найти первообразную функцию 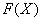  (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.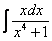

• 

• На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: 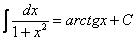 . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.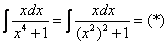

• 

• Проведем замену: 

• 

• 

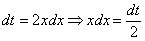
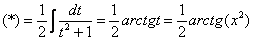
• Неопределенный интеграл найден, константу 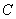  в данном случае добавлять не имеет смысла.

• На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

• 

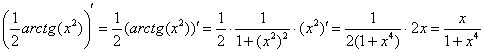
• Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

• Теперь находим несобственный интеграл:

• 

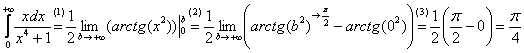
• (1) Записываем решение в соответствии с формулой  . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

• (2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему 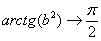  при 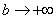 ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

• (3) Получаем окончательный ответ. Тот факт, что 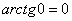  полезно знать наизусть.

• Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

• “ Подынтегральная функция непрерывна на  . “

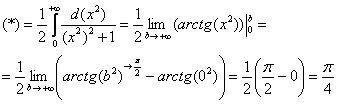• А сейчас два примера для самостоятельного решения.

48Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например,   не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные   до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

Обыкновенные дифференциальные уравнения

Основная статья: Обыкновенное дифференциальное уравнение

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

 или  ,

где   — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по  . Число   называется порядкомдифференциального уравнения.

49 Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при  , а решение отыскивается при  .

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Основные вопросы, которые связаны с задачей Коши, таковы:

1. Существует ли (хотя бы локально) решение задачи Коши?

2. Если решение существует, то какова область его существования?

3. Является ли решение единственным?

4. Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?

Говорят, что задача Коши имеет единственное решение, если она имеет решение   и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки   имеет поле направлений, совпадающее с полем направлений  . Точка   задаёт начальные условия.

Различные постановки задачи Коши

• ОДУ первого порядка, разрешённое относительно производной

• Систем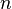а   ОДУ первого порядка, разрешённая относительно производных (нормальная система  -го порядка)

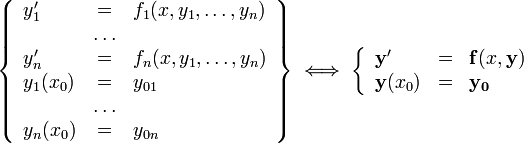
• ОДУ  -го порядка, разрешённое относительно старшей производной