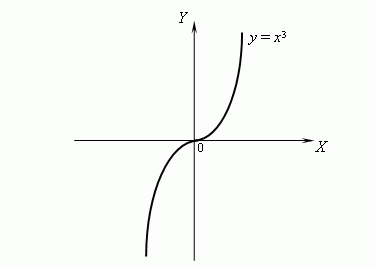Доказательство Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида  ).

Поскольку мы рассматриваем функции   и   только в правой проколотой полуокрестности точки  , мы можем непрерывным образом их доопределить в этой точке: пусть  . Возьмём некоторый   из рассматриваемой полуокрестности и применим к отрезку   теорему Коши. По этой теореме получим:

,

но  , поэтому  .

Дальше, записав определение предела отношения производных и обозначив последний через  , из полученного равенства выводим:

 для конечного предела и

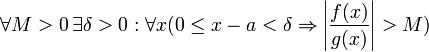 для бесконечного,

что является определением предела отношения функций.

15. Предел отношения двух бесконечно больших величин. (Правило Лопираля)

Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида   и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Условия:

1.  либо  ;

2.  и   дифференцируемы в проколотой окрестности  ;

3.  в проколотой окрестности  ;

4. существует  ,

тогда существует  .

Пределы также могут быть односторонними.

Отношение бесконечно больших

Докажем теорему для неопределённостей вида  .

Пусть, для начала, предел отношения производных конечен и равен  . Тогда, при стремлении   к   справа, это отношение можно записать как  , где   — O(1). Запишем это условие:

.

Зафиксируем   из отрезка   и применим теорему Коши ко всем   из отрезка  :

, что можно привести к следующему виду:

.

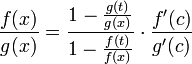Для  , достаточно близких к  , выражение имеет смысл; предел первого множителя правой части равен единице (так как   и   — константы, а   и   стремятся к бесконечности). Значит, этот множитель равен  , где   — бесконечно малая функция при стремлении   к   справа. Выпишем определение этого факта, используя то же значение  , что и в определении для  :

.

Получили, что отношение функций представимо в виде  , и 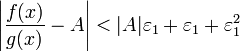 . По любому данному   можно найти такое  , чтобы модуль разности отношения функций и   был меньше  , значит, предел отношения функций действительно равен  .

Если же предел   бесконечен (допустим, он равен плюс бесконечности), то

.

В определении   будем брать  ; первый множитель правой части будет больше 1/2 при  , достаточно близких к  , а тогда  .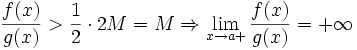

Для других баз доказательства аналогичны приведённым.

16. раскрытие неопределенностей вида ноль на бесконечность, ноль в нулевой

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

(Здесь   - бесконечно малая величина, а   - бесконечно большая величина)

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов  ,  ,   пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

17. Формулы Тэйлора и Маклорена

18. Разложение функции e^x , sin x

Так как (e^x)' = e^x, то производная любого порядка функции e^x равна e^x. При x = 0 функцияe^x и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции e^x имеет вид

Отметим, что для любого вещественного числа x остаточный член

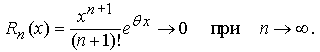
В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем

Следовательно

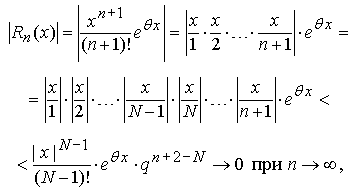
так как q < 1, а величина 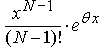  является постоянной при любом n. Таким образом, значения функции e^x могут быть найдены приближенно по формуле:

Разложение функции sin x

Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x

Причем

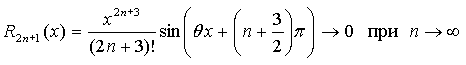
для любого фиксированного вещественного числа x.

19. Разложение функции cos x

Находим последовательно производные от f(x) = cos x.

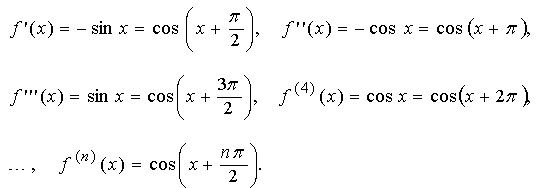
При x = 0 получаем

Следовательно, формула Маклорена для функции cos x имеет вид

Так как  , то

для любого фиксированного вещественного числа x. Таким образом, значения функцииcosx могут быть найдены приближенно по формуле

20. Возрастание и убывание функции

1. Если производная на некотором отрезке больше нуля, то на этом отрезке функция возрастает. 2. Если производная на некотором отрезке меньше нуля, то на этом отрезке функция убывает. 3. Точки, где производная равна нулю или не существует являются критическими точками. В этих точках может быть экстремум функции(то есть максимумы и минимумы). Для их нахождения поступают так: 1) Распологают на координатной прямой критические точки. 2) Внутри каждого промежутка(промежуток знакопостоянства) для произвольной точки найти знак первой производной. 3) Если знак в соседних интервалах разный, екстремум есть, иначе нет. Там, где знак меняется с плюса на минус, будет максимум(не путать с максимальным значением). Там, где знак меняется с минуса на плюс, будет минимум(не путать с минимальным значением). Максимум и минимум можно определить и по второй производной(если она существует). Там, где вторая производная в точке екстремума больше нуля – минимум. Там, где вторая производная в точке екстремума меньше нуля – максимум. 4. Точки, где вторая производная равна нулю или не существует являются критическими точками для нахождения точек перегиба то есть таких точек, где функция меняет вогнутьсть на выпуклость и наоборот. Критические точки разбивают область определения функции на интервалы. В том интервале, где вторая производная больше нуля, функция вогнута. В том интервале, где вторая производная меньше нуля, функция выпукла.

Определение. Функция   называется возрастающей в точке   , если в некоторой   -окрестности этой точки справедливо

для любого   .

Определение. Функция   называется возрастающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   называется убывающей в точке   , если в некоторой   -окрестности этой точки справедливо неравенство

для любого   .

Определение. Функция   называется убывающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   имеет в точке   максимум, если значение   является наибольшим в некоторой двустороней окрестности точки   .

Определение. Функция   имеет в точке   минимум, если значение   является наименьшим в некоторой двусторонней окрестности точки   .

Определение. Функция   имеет в точке   экстремум, если точка   является точкоймаксимума или минимума.

Признаки (достаточные) возрастания и убывания функции   :

Если   на интервале   , то функция   возрастает на этом интервале;

Если   на интервале   , то функция   убывает на этом интервале.

21. Максимум и минимум функции

Наибольшее и соответственно наименьшее значения функции, принимающей действительные значения. Точку области определения рассматриваемой функции, в к-рой она принимает максимум или минимум, наз. соответственно точкой максимума или точкой минимума (см.Максимума и минимума точки).Если нек-рая точка является точкой абсолютного (локального) максимума или минимума, строгого или нестрогого, то значение функции в этой точке наз. абсолютным (локальным), соответственно строгим или нестрогим максимумом или минимумом. Если функция непрерывна на компакте, то она всегда принимает на нем максимальное и минимальное значения.

22. Необходимые и достаточные условия существования экстремума функции.

Необходимое условие экстремума функции.

Функция   может иметь экстремум только в точках, где   или производная не существует. Точка, где   или производная не существует называется критической точкой.

Заметим, что если в точке   выполняется, что   , то это означает, что касательная в данной точке параллельная оси   . Если производная в точке   не существует, то это значит либо касательная вертикальная, либо ее нет в данной точке.

Достаточные условие экстремума функции.

Если функция   непрерывна в точке   и имеет в некоторой окрестности точки   , кроме, быть может самой точки   , конечную производную и если при переходе   через точку  :

 меняет знак с '+' на '-', то точка   -- точка максимума;

 меняет знак с '-' на '+', то точка   -- точка минимума;

 не меняет знак, то точка   не является точкой экстремума.

23. ИССЛЕДОВАНИЕ ФУНКЦИИ НА МАКСИМУМ И МИНИМУМ С ПОМОЩЬЮ ВТОРОЙ ПРОИЗВОДНОЙ Правило исследования функции y = f(x) на максимум и минимум с по мощью второй производной. Если при подстановке критического значения аргумента вторая производная окажется отрицательной, то при этом значении аргумента функция имеет максимум, если положительной — то минимум. Для этого ,в данную функцию y = f(x) вместо аргумента х подставить те критические значения аргумента, при которых функция имеет максимум или минимум. Построить график функции по найденным точкам кривой (точки максимума и минимума функции, точки пересечения кривой с осями Ох и Оу). Исследовать на максимум и минимум с помощью второй производной функции. 4) Вторая производная положительна, следовательно, функция имеет при найденном критическом значении аргумента х—\ минимум (рис. При х—4 функция имеет минимум; 5) найдем максимальное и минимальное значения функции: ^=4 = 43-9-42-f 24-4- 12=4; 6) составим таблицу: V —12 8 _ 4 fe Точка пересече- Максимум функции Минимум функции ния с осью Оу Вторая производная равна нулю, поэтому невозможно установить, что имеет функция: максимум или минимум. Производная знак не меняет, следовательно, функция при х= 1 не имеет ни максимума «и минимума. При х=2 функция имеет минимум; Следовательно, функция при я=1 имеет минимум;

24. Выпуклость, вогнутость и точки перегиба функции

 Если производная  f ' ( x ) функции  f ( x ) дифференцируема в точке ( x₀ ), то её производная называется второй производнойфункции  f ( x )  в точке ( x₀ ), и обозначается  f '' ( x₀ ).  

 

Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

 

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x   ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x   ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

П р и м е р .

Рассмотрим график функции  y = x3 : Эта функция является вогнутой при  x > 0  и выпуклой при  x < 0. В самом деле,  y'' = 6x, но 6x > 0 при  x > 0  и  6x < 0  при  x < 0,следовательно,  y'' > 0 при x > 0 и  y'' < 0 при x < 0, откуда следует, что функция  y = x3 является вогнутой при  x > 0 и выпуклой при x <0. Тогда  x = 0 является точкой перегиба функции  y = x3.

25. Асимптоты функции