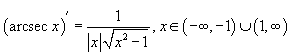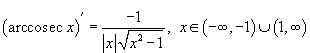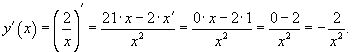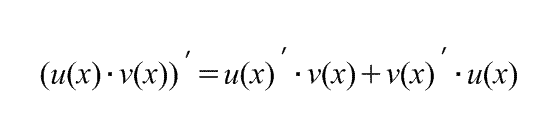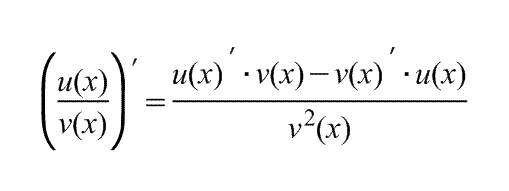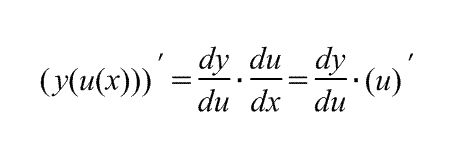ВОПРОСЫ РК 2. 1-8

1. Производные тригонометрических функций

Производные шести тригонометрических функций и, соответственно, шести обратных тригонометрических функций определяются следующими формулами (рядом указана область определения каждой функции):

Пример 1

Вычислить производную функции  . Решение. Применим правило производной сложной функции несколько раз.        По формуле двойного угла        Следовательно, производная равна

2. Логарифмическая производная

Пример

Найти производную функции 

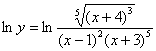
Собственно приступаем к дифференцированию.  Заключаем под штрих обе части:

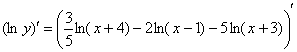
мы используем правило дифференцирования сложной функции  :

условие: 

Окончательный ответ:

3. Таблица производных сложной функции

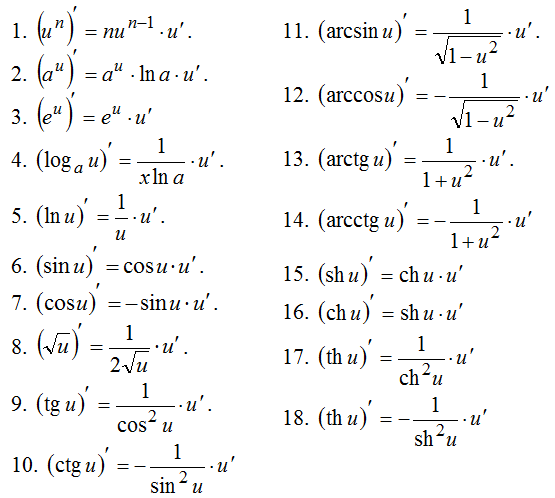
Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а   - целая рациональная функция (смотритеклассификацию элементарных функций), тогда  .

В свою очередь, g(x) также может быть сложной функцией. Например, 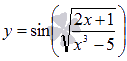 . Условно такое выражение можно обозначить как  . Здесь f – функция синуса,   - функция извлечения квадратного корня,   - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом  .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

Задание. Найти производную сложной функции 

Решение. Используем правила дифференцирования и таблицу производных сложных функций:

Ответ. 

4.

Производная произведения и частного функций

Производная произведения функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и Внимание:  Производная произведения двух функций НЕ РАВНА произведению производных этих функций! Производная частного функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

Пример 1

Найти производную функции  . Решение. Используем правило для вычисления производной частного.

Формулы. Производная произведения. Производная частного. Производная сложной функции. Производная произведения (функции) на постоянную: Производная суммы (функций): Производная произведения (функций): Производная частного (функций):   Производная сложной функции:

5.

6. Таблица производных основных функций

Вычисление производной — важнейшая операция в дифференциальном исчислении. Эта статья содержит список формул для нахождения производных от некоторых функций.

В этих формулах f и g — произвольные дифференцируемые функции вещественной переменной, а c — вещественная константа. Этих формул достаточно для дифференцирования любой элементарной функции.