7. Жазық-параллель пластинкадағы жарықтың интерференциясы (өткінші және шағылған жарықта)

8.Ньютонның жарық сақиналарының радиустарын анықтау (өткінші және шағылған жарықта) Жазық-дөңес линза мен жазық шыны пластинка арасындағы ауа қабатында пайда болатын бірдей қалыңдық жолақтарының мысалына Ньютон сақиналары жатады. Ньютон заманында сақиналардың пайда болуын түсіндіру өте қиын болды. Мәселен, Гук сақиналардың түзілу себебін интенсивтігі әртүрлі шағылған екі шоқтың болуынан көрді, ал Ньютон сақиналардың пайда болуы линзаның қисықтық радиусына тәуелді болатындығын тағайындады. Тек кейіннен (1802 ж) Юнг интерференция ұғымын енгізіп, осы құбылысты түсіндірді. Ньютон сақиналары қисықтығы аз линзаның дөңес беті шыны пластинаның жазық бетімен қайсыбір нүктеде түйіскен жағдайда, бұлардың араларындағы түйісу нүктесінен шеттеріне қарай біртіндеп өсетін, сына пішіндес ауа қабатында пайда болады (2-сурет).

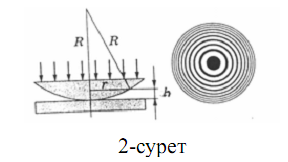
Линзаға монохроматты жарық ағыны тік түсетін болсын. Сонда жарық толқындарының ауа қабатының үстіңгі және астыңғы шекараларынан шағылуы нәтижесінде интерференция байқалады. Шағылған жарықта бақылағанда түйісу нүктесінде қараңғы дақ болады да, ал оны ені кеміп отыратын жарық және қараңғы концентрлік сақиналар жүйесі қоршап тұрады. Орталық қараңғы дақ геометриялық жүріс айырымы нөлге тең болатындықтан және жазық пластина бетінен шағылған кезде жарты толқынның жоғалуы нәтижесінде пайда болады. Өткен жарықтағы интерференциялық көрініс шағылған жарықта байқалатын көрініске қосымша көрініс, яғни бір жағдайдағы жарық жолақтар екінші жағдайда қараңғыға ауысады. 2-суреттен тиісті сақина радиусы үшін өрнекті алуға болады. Ауа қабатының m -і сақинаға сәйкес келетін hm қалыңдығы осы сақинаның rm радиусы және линзаның R қисықтық радиусымен мына қатынаспен байланысқан

= (1)

Δ= 2nh + формуладағы =1 (жарық тік түседі) және n=1 (линза мен пластинка арасында ауа) деп алып, m -і қараңғы сақинаның түзілу шартын табамыз

=2 + = 𝝀 (2)

(2) формулаға (1)-дегі hm мәнін қойып, сақина (шеңбер) радиусы үшін өрнекті аламыз:

= (3)

(3) формуладан m=0 және болғанда, яғни центрде, қараңғы дақ болатындығы келіп шығады. Бұдан кейін интерференция реті неғұрлым үлкен болса, көрші сақиналардың радиустары арасындағы айырмашылық соншалықты аз болады, яғни сақиналар жиірек орналасатын болады. m және R белгілі болса, rm -ді өлшеп, толқын ұзындықты жеткілікті дәл анықтауға болады. Егер түсетін жарық монохроматты болмаса, онда шағылған жарықта әртүрлі толқын ұзындықтарына әртүрлі rm сәйкес келеді де экранда түрлі-түсті сақиналар жүйесі байқалатын болады. Өткен жарықта, әрине, шағылған жарықтағы түске қосымша түстер көрінетін болады.

9.Ньютон сақиналары көмегімен жарық толқынының ұзындығын анықтау. Егер жазық, шыны пластинканың үстіне жазық-дөңес линза қойылса, онда олардың арасында сына пішіндес ауа қабаты пайда болады (16, а-сурет). Енді осындай системаға, пластинка бетіне шамада перпендикуляр бағытта, монохромат жарық түссе, сонда жарық толқындары осы сына пішіндес ауа қабатының үстіңгі және төменгі шекараларында шағылады да өзара интерференцияланады, осының нәтижесінде лннза мен пластинка тиісіп тұрған нүктеде қара коңыр дақ пайда болып, оны концентр жарық және кара коңыр шеңберлер қоршап тұрады, олар центрден қашықтаған сайын жиі тарта береді. Осы шеңберлер бірдей қалындық жолақтары болып табылады. Бұларды бірінші рет Ньютон зерттеген, сондықтан олар Ньютон сақиналары деп аталады. Ньютон сақиналарының өлшемдері мен орынын анықтау қиын емес. 16, б-суретте жазық пластинканың үстіне қойылған жазық-дөңес линзаның кимасы кескінделген. Линзаның кисықтық радиусы R мен берілген қара коңыр шеңбердің   радиусы арасында қатынас бар. Суретке қарағанда

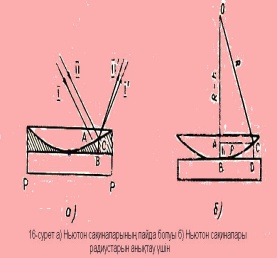
                             немесе 

һ — өте аз шама болғаңдықтан һ-ты елемесе де болады, сонда жуықтап алғанда  бұдан

Жоғарыда айтылғандай жарық пластинканың бетіне перпендикуляр бағытта түскенде соsr = 1 болады, ауаның n'=1. Сонда  формула бойынша жолдың оптикалық айырмасы мынаған тең:

 

Енді һ- тың орнына,  формула бойынша онын мәнін қойсақ мынау шығады:

 

Ал қара қоңыр шеңберлер түзілу үшін      болуға тиіс, сонда бұл шеңбердің радиусы былай өрнектеледі:

мұндағы к=1, 2, 3... Жарық шеңберлер түзілу үшін  болғуа тиіс, сонда мұндай шеңбердің радиусының өрнегі мынадай болады:

 

мүнда да к =1, 2, 3...

Формулаларға карағанда неғүрлым жарық толқыны қысқа болса, соғүрлым Ньютон сақиналарының радиусы кысқа болады. Егер ақ жарық түсірілсе, онда сақиналар түрлі түсті болады да, олардың ішкі жиектері күлгін түсті болады. Шағылған жарықта бақылағанда орталық дақ қара коңыр болады, өйткені интерференциялану нәтижесінде сәулелер бірін-бірі жойып жібереді. Өткінші жарыкта бақылағанда орталық дақ жарық болады.

Жоғарыда айтылғандай тәжірибе жасап, Ныотонның сақиналарының біреуінің   радиусын өлшеп тауып, R-дің мәні мәлім болса, монохромат жарық толқынының ұзындығын, мысалы формула бойынша, есептеп табуға болады.

Ақшыл сақиналардың радиустары:

Қара қоңыр сақиналардың радиустары:

Интерференцияны өткінші жарықта да бақылауға болады. Бұл жағдайда өткінші жарықтың интерференциалық максимумдары шағылған жарықтың интерференциалық минимумдарына сәйкес келеді және керісінше.

10.Интерференциялық аспаптар. Интерференция құбылысының өндірісте қолдануы . Жарықтың интерференция құбылысы мөлдір орталардың сыну көрсеткіштерін,спектрлік сызықтардың толқын ұзындықтарын,бұрыштарды т.с.с. дәл өлшеулер үшін қолданылатын оптикалық құралдар,яғни интерферометрлер электромагниттік сәуленің негізгі сипаттамаларын зерттеу үшін пайдаланылады. Сондықтан интерферометрлердің оптикалық схемасы кейбір қосымша талаптарды қанағаттандыруы тиіс. Мәселен,өлшеу дәлдігін арттыру үшін жүріс айырымын едәуір өсіру керек болады,яғни интерферометрлердің жоғары реттері жағдайында жұмыс істеуге тура келеді. Барлық белгілі интерференциялық аспаптарды негізінен екі топқа бөлуге болады: екі сәулелік және көп сәулелік. Пластинканың алдыңғы және артқы беттерінен шағылған екі сәуленің интерференциясы іске асырылғанда, бұл екі сәулелік интерферометр болады. Егер пластинка қалың болса,онда интерференцияланатын бір және екі сәулелер едәуір қашықтыққа ажыратылады және бұлардың кез−келгеніне зерттелетін затты ендіруге болады. Екі сәулелік интерференцияны іске асыру үшін жиіліктері бірдей екі монохроматты толқын болуы қажет. Екі сәулелік интерферометрге Жомен интер−і, Рождественский, Майкельсон интерферометрлері жатады. Көп сәулелік интерференциялық құралдар көп жарық шоқтарының интерференциясы негізінде құрастырылған және бұлардың түрлері онша көп емес. Оған Фабри−Перо, Люммер−Герке интерферометрі жатады. Оптикада интерференцияны іске асыру үшін толқындарды алу екі жолмен орындалады: 1) толқын амплитудасын бөлу; 2) толқын шебін (фронтын) бөлу.

Жамен интерферометрі. Бұл интерферометр бірдей екі жазық параллель қалыңдығы және сыну көрсеткіші шыны пластинадан тұрады. жарық көзінен жарық бірінші пластинаның алдыңғы бетіне түседі де жартылай шағылу және сыну нәтижесінде, бірінен бірі қайсыбір қашықтықта болып, екінші пластинкаға баратын, 1 және 2 сәулелері пайда болады. Екінші пластинада шағылып және сынғаннан кейін, одан төрт сәуле шығады; бұлардың екеуі интерференцияланады. Бұлардың арасындағы жүріс айырымы: .

Интерферометрдің бірінші пластинасын монохроматты жарықтың параллель шоғымен жарықтандырғанда кез-келген қос сәуле үшін бірдей жүріс айырымы пайда болады. Сәулелер пластиналардың екеуінен шағылғаннан кейін біркелкі жарықтанған интенсивтігі жүріс айырымының мәніне тәуелді өріс алынады. толқын ұзындықтардың бүтін санына тең болған жағдайда интенсивтік максимум, жүріс айырымы ұзындықтардың тақ санына тең болған жағдайда-интенсивтік минимум болады. Жолақтар арасындағы бұрыштық қашықтық бұрышының өзгерісіне тәуелді. Сонда жүріс айырымы -ға өзгереді, яғни

немесе

Жамен интерферометрінің пластиналары арасындағы 1 және 2 сәуле шоқтарын үлкенірек қашықтыққа ажырату үшін пластиналар қалың етіліп (2см-ге дейін) жасалады. Бұл шоқтардың біреуінің жолына қоршаған ортаның сыну көрсеткішіне қарағанда сыну көрсеткіші басқаша қандай бір зат қабатын ендіруге, сөйтіп бұлардың арасында қосымша жүріс айырымын туғызуға мүмкіндік береді. Рождественский интерферометрі. Жамен интерферометрінің өзгертілген түрі. Ол төрт айнадан тұрады, бұлардың екеуі толық шағылдырушы, қалған екеуі жарық шоқтарын бөлушілер қызметін атқаратын жартылай мөлдір. айналарының шағылдыру коэффициенті 50% шамасында болады, өйткені 1 және 2 жарық шоқтарының интенсивтіктері шамамен бірдей болғаны жөн.

Рождественский интерферометрі негізінен газдар мен булардың жұтылу сызықтары маңайындағы сыну көрсеткішіне дәл өлшеулер үшін қолданылады.

Майкельсон интерферометрі. Бұл интерферометр ғылым мен техниканың дамуында іргелі роль атқарды. Оның көмегімен жарық толқынының ұзындығы алғаш өлшенді, спектрлік сызықтардың нәзік түзілісіне бірінші жүйелі зерттеулер жүргізілді, спектрлік сызықтардың толқын ұзындықтарын эталондық метрмен тікелей салыстыру бірінші орындалды. Осы интерферометр көмегімен Майкельсон-Морлидің-жарық жылдамдығының Жер қозғалысына тәуелсіздігі дәлелденген атақты тәжірибесі іске асырылды.

11.Френельдің аумақ әдісі. Аумақ пластинасы. Векторлық диаграмма әдісін Гюгенс-Френель дифракциялық интегралын есептеу үшін қолданамыз. Ол үшін Френель аумағын көптеген концентрлік сақиналарға бөлеміз. Бөлуді аумақшалардың аудандары шаамамен бірдей болатындай, ал аумақшалар саны жеткілікті үлкен болатындай етіп іске асыруға болады. Осы жағдайда аумақшалардың үлестері ұзындықтары бірдей, бірақ абсцисса осіне көлбеулік бұрыштары әртүрлі векторлармен кескінделеді. Бірінші ж/е соңғы векторлар бір-біріне қатысты π бұрышқа бұрылған. Радиус өскен сайын аумақша үлесі , ∑ бетіне нормаль мен бақылау нүктесіне бағыт арасындағы бұрыштың өсуі себепті аздап кемиді. Френельдің бірінші аумағының ,ж/е нөлінші ж/е бірінші аумақтаррының бірігіп кескіндейтін вектор тұрғызылады.

Френель дифракциясы деп бөгетке сфералық н/е параллель толқын түседі, ал дифракциялық сурет бөгеттен шектеулі қашықтықта орналастырылған қалқада бақыланады.

S нүктелік жарық көзінен шығатын ∑ жарық толқыны дөңгелек тесігі бар ММ' қалқаға түседі. (сурет2). Р нүктесіндегі интенсивтік тессік ауданына Френель аумағының тақ н/е жұп саны сыюына байланысты, толқындық шептің толық ашық болғандығы интенсивтігінен үлкен н/е кіші болады.

Толқындық шепті тақ ж/е жұп Френель аумақтарына бөлуге болатындығы қалаған аумақтарды бөліп алуға жарайтындай дифракциялық экран жасауға мүмкіндік береді. Тек тақ н/е тек жұп аумақтардың қосынды әрекеті толық ашық толқындық шептің жасайтын әрекетінен артық болады. Егер экранда тек тақ Френель аумақтарын ашса, онда осы аумақтардан қоздырылатын тербелістердің амплитуда векторларының бәрі бағыттас болады да, бұлардың қосындысы модулі б/ша ж/е векторларынан көп есе басым түсетін векторды береді. Осындай қалқаны аумақтық пластинка деп атайды

12.Гюйгенс-Френель принципы, оның интегралдық түрі мен мәні. Зоналық пластиналар. Дөңгелек саңылаудағы Фраунгофер дифракциясы. Жарық толқынының геометриялық көлеңке аймағына өтуін Гюгенс принципі түсіндіреді. Бірақ оның принципі амплитуда жайлы дерек бермейді,яғни әр түрлі бағытта таралатын толқындардың интенсивтігін сипаттамайды. Гюгенс принципін Френель екінші реттік толқындардың интерференциясы жайындағы көрініспен толықтырды. Осылай Гюгенстің енгізген екінші ретті толқындары интерференциялануы арқасында қорытқы толқынның интенсивтігі максимум болатын бет болды. Екіші реттік толқындардың амплитудалары мен фазаларын ескеру кеңістіктің кез−келген нүктесіндегі қорытқы толқынның амплитудасын табуға мүмкіндік берді. Осылай толықтырылған Гюгенс принсипі Гюгенс−Френнль принципі д.а. Ол толқынның интенсивтігінанықтағанда,дифракцияны есептегенде қолданылады. Ол толқындық оптиканың негізгі принципі болып табылады. Фраунгофердифракциясының Френель дифракциясынан негізінде айырмашылығы жоқ. Егер дифракциялаушы қалқадан бақылау нүктесіне дейінгі қашықтық оның мөлшерлеріне салыстырғанда өте үлкен болса, онда бақылау нүктесіне дейінгі екінші реттік толқындарды жазық деп санауға болады. Фраунгофер әдісі бойынша дифракциялық сурет мөлдір емес қалқамен біраз бөлігі бөгелген жазық жарық толқындары жиналатын линзаның бас тоғыстық жазықтығында бақыланады. Сонымен мұнда параллель сәулелер түзетін Фраунгофер дифракциясы деп аталатын дифракциялық сурет қарастырылады. Фраунгофер дифракциясы оптикалық аспаптардың жұмыс істеуіне қатысты көптеген мәселелерді шешкен кезде кең түрде қолданылады. Фраунгофер дифракциясы жағдайларына жақын жағдайларды жарықтың нүктелік көзін линза тоғыстығына орналастырып және жарықты екінші линза көмегімен, оның тоғыстық жазықтығына орналастырылған қалқаның қайсыбір нүктесіне жинап, іске асыруғаболады. Бұл нүкте жарық нүктесінің кескіні болады. Линзалардың аралығына әртүрлі тесіктері бар қалқалар қойып, дифракциялық суреттің сипатын өзгертетін боламыз. Тесіктердің пішіні мен мөлшеріне қарай жарықтың бір бөлігі жарықтың бастапқы бағытымен түрліше бұрыш жасап таралады да бақылау қалқанының әртүрлі нүктелерінде жиналатын болады. Осының нәтижесінде қалқадағы кескіннің жарықталуы нүктеден нүктеге өзгеретін дақ түрінде болады. Фраунгофер дифракциясын бақылыу схемасы 1-суретте көрсетілген.

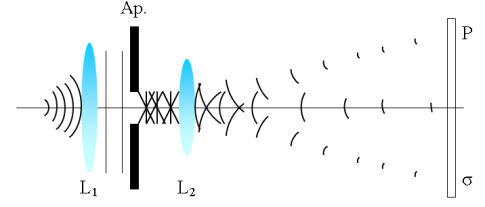
S нүктелік жарық көзінен шығарылған жарықты L1 линза жазық толқынға айналдырады, ол мөлдір емес қалқадағы тесік арқылы өтеді. Линза өзінің бас тоғыстық жазықтығының әртүрлі бөліктеріндегі тесіктен өткен барлық сәулелерді, соның ішінде дифракция нәтижесінде бастапқы бағытынан ауытқыған сәулелерді де жинайды. L2 Линзаның тоғыстық жазықтығындағы жарықталудың үлестірілуін зерттеп дифракциялық суреттің көрімділігін анықтауға болады. Диф/я құбылысын жарықтың толқындық теориясы б/ша толық түсіндіруге болады.Толқындық беттің әрбір нүктелерінің айналасында пайда болған элементар толқындар бір-бірімен қосылысып интерференцияланады, сонда қорытқы сыртқы орауыш бетте толқынның едауір интенсивтігі болады. Элементар толқындар мен интерференция жайындағы идеялардан жарықтың толқындық теориясының негізгі принципі –Гюгенс-Френель принципі шығады. Бұл принцип б/ша толқындық беттің алдыңғы жағындағы бір нүктедегі тербелісті табу үшін сол нүктеге толқындық беттің барлық элементтерінен келген тербелістерді тауып, одан соң олардың амплитудалары мен фазаларын есепке ала отырып, оларды өзара қосу керек.

Френенль зоналар методын қолданды. Бұл метод толқындық бетті ойша дөңгелек зоналарға бөлуге ж/е олардан таралып бір-біріне қосылысып интерференцияланған элементар толқындардың амплитудалары мен фазаларын есепке алуға негізделген. S жарық көзінен жарық толқындары таралып сфералық толқындық беттер түзілсін , сонда олардың біреуі ∑-мен белгіленген бет болсын. Жарық толқынының P нүктедегі әсерін анықтау үшін Френельше сол ∑ толқындық бетті ойша дөңгелек зоналарға бөлеміз. Көршілес зоналардың сәйкес нүктелерінен P нүктесіне келген жарық тербелістерінің жол айырмасы тең. Гюгенс-Френель интегрлы: : .

P нүктесіндегі толық өріс ∑ бетінің барлық элеметтерінен келетін екінші реттік толқындар өрістерінің суперпозициясы.

Фраунгофер н/е параллель сәулелер дифракциясы деп бөгетке жазық толқын түседі, ал дифракциялық сурет бөгет арқылы жарық жолына қойылған жинағыш линзаның фокалдық жазықтығына орналастырылған қалқада бақыланады.

Шексіз ұзын, ені b саңылауға жазық жарық толқыны нормаль түсетін болсын. Саңылаудан кейін линза, ал оның фокалдық жазықтығында L бақылау қалқасы қойылған. Тербелістердің нүктедегі амплитудасын есептеу үшін толқындық беттің ашық бөлігін ендері бірдей саңылау нүктелеріне параллель жіңішке жолақтар түріндегі аумақтарға бөлеміз, осы аумақтардың әрқайсысы нүктесіне келіп жететін толқындар көзі ретінде қарастырылуы тиіс, ж/е көрші аумақтардан шығарылатын толқындардың фазалары бірдей шамаға өзгеше болады. Қалқаның кез-келген нүктесіне барлық аумақтардан келетін тербелістер амплитудаларының алгебралық қосындысын арқылы белгілеп: .

Дөңгелек тесіктегі Фраунгофер дифракциясының практикада маңызы зор, оптикалық аспаптардағы линзалар мен объективтердің оправалары ж/е диафрагмалар дөңгелек пішінді. Дифракциялық сурет кезектесіп келетін қараңғы ж/е жарық сақиналармен қоршалған орталық жарық дақ түрінде болады. Ең бірінші қараңғы сақинаның минимумы дифракцилық суреттің центрінен мынадай бұрыштық қашықтықта болатындығы алынады: . тесік диаметрі неғұрлым үлкен б/са, соғұрлым дифракциялық суреттің мөлшері кіші болады. Тесік арқылы өтетін жарық ағынының басым бөлігі орталық жарық дақ аймағына түседі.