Формы текущего, промежуточного и итогового контроля

Текущий контроль:

• Самостоятельные работы

• Индивидуальные задания

• Опрос студентов

Промежуточный контроль:

• Индивидуальная работа

• Домашняя контрольная работа

• Тестирование по курсу

Итоговый контроль:

• Экзамен

Методические указания к самостоятельной работе студентов

Студенты испытывают некоторые проблемы в усвоении курса “Теория алгоритмов” в целом, а именно в усвоении подхода Тьюринга к формализации понятия алгоритма по причине того, что в настоящее время снизилось количество часов отводимых на аудиторную работу. Упор приходится делать на самостоятельную работу студентов.

В программе курса приведено минимально необходимое время для работы студента над темой. Самостоятельная работа включает в себя чтение лекций и рекомендованной литературы, решение задач домашнего задания, предлагаемого студентам на лекциях и практических занятиях, разбор проблемных ситуаций, написание курсовых работ. Руководство и контроль за самостоятельной работой студента осуществляется в форме индивидуальных, консультаций

Для активизации самостоятельной работы студентов и экономии времени отводимого на лекционный курс, ряд тем выносится на самостоятельное изучение. Самостоятельная работа со студентами проводится в часы самостоятельной работы в форме консультаций. Распределение часов руководства самостоятельной работой учитывает важность рассматриваемой темы и возможную сложность при освоении ее студентами.

Индивидуальные занятия

Индивидуальные занятия заключаются в самостоятельном выполнении студентами домашней контрольной работы, а также домашних заданий по соответствующим разделам дисциплины.

Темы курса, по которым предусмотрена домашняя контрольная работа:

1. Построение алгоритмов и их реализация в машине Тьюринга.

2. Примитивно рекурсивные функции.

3. Примитивно рекурсивные предикаты.

4. Примитивно рекурсивные отношения.

5. Примеры алгоритмов в математике.

Примерная тематика курсовых работ

1. Формальные грамматики. Классификация Хомского. Грамматики типа 2 и их использование при построении трансляторов.

2. Понятие неоднозначности в теории грамматик. Привести примеры неоднозначных грамматик и неоднозначного вывода в них.

3. Алгоритмические проблемы в теории грамматик.

4. Основная идея доказательства существования универсальной машины Тьюринга и блок-схема ее построения.

5. Общая схема доказательства эквивалентности машин Тьюринга и рекурсивных функций.

6. Связь формальных грамматик и конечных автоматов.

7. Сравнение сложности вычислений на одноленточной и многоленточной машинах Тьюринга на примере распознавания палиндромов в двухбуквенном алфавите.

Методические рекомендации по организации изучения дисциплины

Контрольные и самостоятельные работы

Контрольная работа №1

По теме «Примитивно рекурсивные функции, отношения и предикатыы»

ВАРИАНТ 1

1. Пусть f – примитивно рекурсивная n-местная функция, а n-местная функция g, такая, что "x₁, x₂, x₃, x₄,…, x_nN g(x₁, x₂, x₃, x₄,…, x_n)=f(x₃, x₁, x₂, x₄,…, x_n). Докажите, что функция g примитивно рекурсивная.

2. Функция y=f(x) определена «с перебором случаев»:

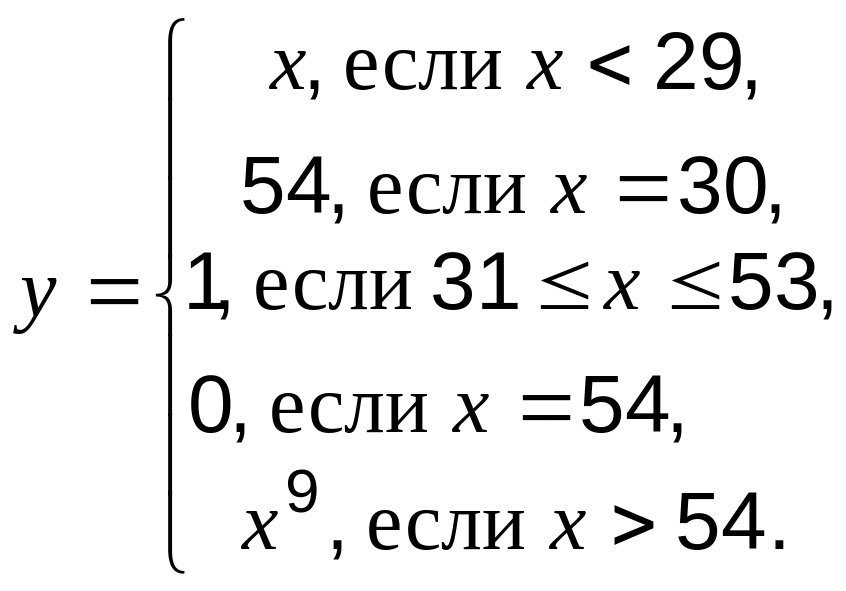
Докажите, что функция y=f(x) примитивно рекурсивная.

3. Предикаты P(x) и Q(x) примитивно рекурсивны. Определим: (PQ)(x)P(x)Q(x) для всех xN, где логическая связка  задана следующей таблицей истинности:

P	Q	PQ
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Докажите, что предикат (PQ)(x) тоже примитивно рекурсивный.

4. Определите последовательности, заданные по схеме рекурсии

a) b)

ВАРИАНТ 2

1. Пусть f – примитивно рекурсивная 4-местная функция, а 7-местная функция g, такая, что "x₁, x₂, x₃, x₄, x₅, x₆, x₇N g(x₁, x₂, x₃, x₄, x₅, x₆, x₇)=f(x₂, x₄, x₄, x₂). Докажите, что функция g примитивно рекурсивная.

2. Функция y=f(x) определена «с перебором случаев»:

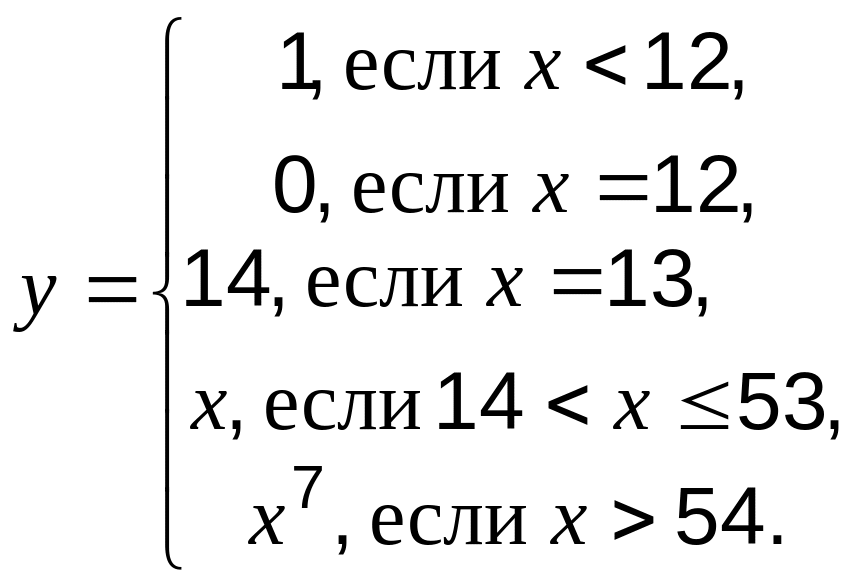
Докажите, что функция y=f(x) примитивно рекурсивная.

3. Предикаты P(x) и Q(x) примитивно рекурсивны. Определим: (PQ)(x)P(x)Q(x) для всех xN, где логическая связка  задана следующей таблицей истинности:

P	Q	PQ
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Докажите, что предикат (PQ)(x) тоже примитивно рекурсивный.

4. Определите последовательности, заданные по схеме рекурсии

a) b)