14.Идентификациялау әдістері: тура әдістері, параметрлі және параметрлі емес идентификация.
Сызықты объекттің динамикалық сипаттамаларын тәжірибелі жолмен анықтау әдістерін үшке бөлуге б/ы.Тура әдістер кірістегі арнайы сигналдарды қолданады:өтпелі ф-мен идент-ға сатылы сигнал, импульсті – өтпелі ф-мен идент-ға импульсті сигнал, жиілік сипаттаманы анықтауға гармоникалық сигнал. Және келесідей сипаттамалармен анықталады: жиілік аймағында – амплитудалық және фазалық сипаттамалары, уақыт аймағында – импулсты өтпелі және өтпелі функциялары. Бұл сигналдардың ішінде сатылы сигнал қолдануға қарапайым б/п келеді. Импульсті сигналды қолдану біршама техникалық қиындықтарға тіреледі. Сонд-н бұл әдіс сызықтандырылған жүйелерге қолдануға б/майды.
Параметрлік әдіс- модельдің белгісіз параметрлерін анықтауды айт-з. Бұл әдіспен есепті шығаруда сәйкессіздік критерийді минимумдау к/к. Параметрлік емес әдіс- белгісіз функцияларды анықтауды айт-з.
17.Сызықты динамикалық объекттерді параметрлік идентификациялау.
Параметрлік
идент модель параметрлерімен анықталады.
Және оны процесс кезінде бағалау к/к.
Ал бағалау үшін сәйкессіздік функционалын
минимумдау к/к. Оны екі жағдайда
қарастыруға б/ды: статикалық сызықты
объект ж/е динамикалық сыз об. Статикалық
сыз об-те 1-ші модль құрылымы таңдалады:
.
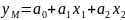2-ші тәжірибе жүргізгендеобъект туралы
ақпаратты
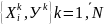анықтау к/к.
-
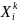кірістің күйі,
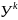-реттелетін
шама,
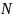-тәжірибелер
саны.Tәжірибелік
нәтижелерді қолданып, теңдеуді шешміз:
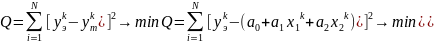
Әр
бір коэффициенттері б/ша туындыларын
тауып, нөлге теңестіреміз:
.
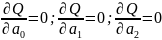Динамикалық
сыз об дифференциалдық теңдеулер
қолд-ды.
.
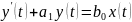Сәйкессіздік
фунцияны құрастырамыз:
Осыдан
орта квадратты шығарамыз: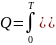
.
яғни
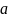ж/е
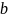б/ша минимумдаймыз. Мұнда барлық белгісіз
параметрлердің туындыларын тауып,
сызықты теңдеулер жүйесін аламыз:
.
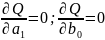Бұл жүйенің шешімі минимумдау есебінің
шешімі б/п т/ды.
18. Сызықты динамикалық объекттерді параметрлі емес идентификациялау.
Параметрлі емес үлгі көбіне үздіксіз функциямен анықталады. Бірақ ол нүктелеремен немесе белгілі функциялар жүйесі бойынша қатармен берілуі мүмкін.Сызықты динамикалық нысанның спецификасы оның бірлік импульсты әсерге реакциясымен анықталады.Сондықтан параметрлі емес үлгі импульсты өтпелі функ-мен анықталады.Стационарлы жағдайда бұл функция тек қана бір айнымалыга – уақыттан тәуелді: g = g(t), 0 <= t <∞.
Жүйеге x(t) әсер берілгенде сызықты жүйенің y(t) сипаттамасы осы функция көмегімен біртекті келесідей анықталады
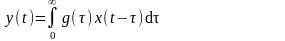
t< 0 болғандаx(t) = 0 болады.Бұл өрнек жиймаинтегралы д.а
g(t) импульсты өтпелі функцияны анықтау үшін нысанның x(t) кірістерінің өлшеулерін оның өмірінің барлық уақытында, яғни t=0 –ден t=∞ дейін өзгергендеалуымыз керек екендігін формуласынан көреміз. Салмақты функциясының қасиеті lim g(t) = 0.
t∞
бұл шарт тұрақты жүйенің импульсты әсерден кейін өзінің бастапқы қалпына оралад. Сонда, t>Tg болғанда |g(t)| <= α*gmax,
Tg уақыт моментінен бастап, салмақты функция 100α-пайызды диапазоннан шықпайды (әдетте α = 0.05).
жийма
интегралын келесі түрде жазамыз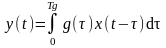
Бұл әдістерді көп қолдана алмаймыз:
нысандағы процестердің кәдімгідей тәртібінің бұзылу себебінен нысан кірісне арнайы түрдегі әсерлерді беру мүмкін емес;
көбіне осы әсерлерге бақыланбайтын бөгеттер қосылады, сондақтан нысанның динамикалық сипаттамаларын типтік кіріс сигналдары бойынша анықтау мүмкін болмайды.