4)Переход к равенствам в задаче использования сырья и задаче составления рациона.

Задача составлении рациона

При откорме каждое животное ежедневно должно получить не менее 9 ед питательного вещества S1 .Не менее 8 ед питательного вещества S2. Не менее 12 ед питательного вещества S3

Для составления рациона используются два вида корма.Содержание количества единиц питательного вещества в 1 кг корма привидено в таблице

Питательные вещества	кол-во ед питательного вещества в 1 кг
	корм 1	корм 2
S1	3	1
S2	1	2
S3	1	6
Стоимость 1 кг	4	6

Составить дневной рацион нужно питательного вещества, затраты---min

Обозначим через X1,X2 соответсвтующее количество кг корма 1 и 2 вида в дневном рационе .Если корм 1 не используется, то корм 1 X1=0.В противном случае X1>0 (аналогично для X2).

Задача является многовариантной , так как X1 и X2 могут принимать бесконечное множество решений.

Z=4X1+6X2-min

3X1+X2>=9

X1+2X2>=8

X1+6X2>=12

Обобщенная задача составления рациона

Пусть в рационе ‘m’-видов питательные вещества в кол-ве не менее чем B_i (i=1,n) используется ‘n’-видов кормов.

Обозначим через A_ij(i=1,m; j=1,n) кол-во ед i-питательного вещества содержится в ед j-корма.

Cj-( j=1,n) стоимость единицы j-го корма

Xj- ( j=1,n) кол-во j-го корма в дневном рационе.

Задача min стоимости затрат на дневной рацион

Z=С1X1+C2X2+….+CjXj-min

A11X1+A12X2+…..+A1mXn>=B1

A21X1+A22X2+….+A2mXn>=B2

Am1X1+Am2X2+….+AmnXn>=Bnn

Xj>=0 (j=1,n)

В математических моделях если сырье используется или в дневном рационе должно должно содержаться точное количество питательного вещества , то ограничение можно выразить в виде равенства. Перейдем к равенствам в задаче:

Задача составления рациона .Все неравенства содержащие знаки >=,= для перехода к равенству необходимо из левых частей вычесть неотрицательные дополнительные переменные

Z=C1X1+C2X2+…+CjXj+0*X _n+1 0*X_n+2 +….+0*X _n+m -min

A11X1+A12X2+…..+A1nXn-Xn+1=B1

A21X1+A22X2+…..+A2nXn-Xn+2=B2

………………………………………….

Am1X1+Am2X2+…..+AmnXn-Xn+m=Bm

Правые части неравенства\уравнения для любой системы ограничения можно считать неотрицательными, если для любого неравенства Bk<0 то (*(-1)) поменяем знаки неравенства.

Задача составления сырья

Пусть при выпуске ‘n’-видов продукции использовать ‘m’-видов сырья.

Обозначим через Si(i=1,m) виды сырья

Bi-запасы сырья i-вида

Pi (j=1,n)- виды продукции

Aij (i=1,m)-кол-во ед i-го сырья идущее на изготовление j-продукции.

Cj-величина прибыли , полученная от реализации единицы j-ой продукции.

Пусть Xj-это кол-во j-продукции , которую нужно произвести , тогда математическая модель задачи имеет вид

Виды сырья	Запасы сырья	кол-во ед i-сырья идущ на производство j-продукции
		P1	P2	…..	Pn
S1	B1	A11	A12		A1n
S2	B2	A21	A22		A2n
S3	Bm	Am1	Am2		Amn
Прибыль		C1	C2		Cn

В математических моделях если сырье используется или в дневном рационе должно должно содержаться точное количество питательного вещества , то ограничение можно выразить в виде равенства.Перейдем к равенствам в задаче:

задача использования сырья

Z=C1X1+C2X2+…+CnXn+0*X _n+1 0*X_n+2 +….+0*X _n+m -max

A11X1+A12X2+…..+A1nXn+Xn+1=B1

A21X1+A22X2+…..+A2nXn+Xn+2=B2

………………………………………….

Am1X1+Am2X2+…..+AmnXn+Xn+m=Bm

Где Xj>=0 (j=1,n,n+1,….n+n)

Где Xn+i,( i=1,n)-дополнительная переменные и соответствующии им коэффициенты в целевой функции =0.

Правые части неравенства\уравнения для любой системы ограничения можно считать неотрицательными, если для любого неравенства Bk<0 то (*(-1)) поменяем знаки неравенства.

5. Оснавная задача линейного программирования

 

Основная задача линейного программирования состоит в следующем. Задана система 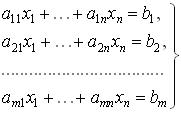(6.10) m линейных алгебраических уравнений с n неизвестными x₁,...,x_n и линейная форма относительно этих же неизвестных: F = c₁x₁ + ... + c_nx_n. (6.11) Требуется среди всех неотрицательных решений системы (10) выбрать такое, при котором форма F принимает наименьшее значение (минимизируется). Определение: Система (6.10) называется системой ограничений данной задачи. Сами равенства (6.10) называются ограничениями-равенствами. Отметим, что кроме ограничений-равенств в основу задач входят также ограничения-неравенства x₁≥0,...,x_n≥0 Определение: Всякое неотрицательное решение x₁⁽⁰⁾,...,x_n⁽⁰⁾(x_i⁽⁰⁾≥0; i=1,...,n) системы (6.10) назовем допустимым. Допустимое решение часто называют планом задачи линейного программирования. Определение: Допустимое решение системы (6.10), минимизирующее форму F, назовем оптимальным. Рассмотрим следующие ограничения системы (6.10). Задача имеет смысл лишь в том случае, когда система (6.10) совместна, то есть когда (согласно теореме Кронекера-Капелли) ранги основной и расширенной матриц системы совпадают. Этот общий ранг r не может превосходить числа n неизвестных. При r= n решение x₁⁽⁰⁾,...,x_n⁽⁰⁾ системы (6.10) единственно. Если это решение допустимо, то оно является оптимальным, так как никаких других решений вообще нет. Если же среди чисел x_i⁽⁰⁾ имеется хотя бы одно отрицательное, то задача не имеет решения. Таким образом, интерес представляет лишь случай r < n, и только он будет нами рассматриваться в дальнейшем. Каждую задача линейного программирования можно свести к форме основной задачи. Для этого нужно: 1. Уметь сводить задачу максимизации к задаче минимизации. 2. Уметь переходить от ограничений, заданных в виде неравенств, к некоторым им эквивалентным ограничениям-равенствам. Покажем, как это сделать. 1. Очевидно, что форма F достигает наибольшей величины при тех же самых значениях неизвестных x₁⁽⁰⁾,...,x_n⁽⁰⁾, при которых форма F₁ = -F достигает наименьшей величины. Следовательно, максимизация формы F равносильна минимизации формы F₁ = -F. Тем самым задача максимизации сводится к задаче минимизации. 2. Допустим теперь, что среди ограничений задачи имеется некоторое неравенство. Его всегда можно записать в виде a₁x₁ + a₂x₂.+ ... + a_nx_n + β ≥ 0 (6.12) Введем новую, так называемую добавочную, неизвестную, связанную с неизвестными x_1,...,x_n уравнением x_{n+1 =} a₁x₁ + a₂x₂.+ ... +a_nx_n + β. (6.13) Очевидно, что условие неотрицательности величины x_n+1 эквивалентно выполнимости неравенства (6.12). Иными словами, если система x₁⁽⁰⁾,...,x_n⁽⁰⁾,x_n+1⁽⁰⁾ неотрицательных значений x_1,...,x_n,x_n+1 удовлетворяет уравнению (6.13), то система x₁⁽⁰⁾,...,x_n⁽⁰⁾ удовлетворяет неравенству (6.12). И обратно, если величины x₁⁽⁰⁾,...,x_n⁽⁰⁾ неотрицательны и удовлетворяют неравенству (6.12), то величина x_{n+1 =} a₁x₁ + a₂x₂.+ ... +a_nx_n + β, найденная из уравнения (6.13), окажется неотрицательной. Итак, ограничение-наравенство (6.12) эквивалентно ограничению-равенству (6.13). Следовательно, ценою введения в задачу добавочных неизвестных удается все ограничения-неравенства заменить ограничениями-равенствами. При этом число добавочных неизвестных равно числу ограничений-неравенств в исходной задаче.