1. Интерполяционная формула Лагранжа.

Пусть известны значения некоторой функции f(x) в n различных точках , .

Например, эти значения получены из эксперимента или найдены с помощью достаточно сложных вычислений.

На отрезке [a, b] надо проинтерполировать функцию f(x)

Часто для решения этой задачи строится алгебраический многочлен степени (n-1), который в точках принимает заданные значения, т.е. , и называется интерполяционным. Точки , , называются узлами интерполяции.

Приближенное восстановление функции f по формуле называют интерполяцией функции f.

- интерполяционная формула Лагранжа.

Найдем :

=> ; … .

Формулу Л. можно записать следующим образом:

Погрешность интерполяции:

, где - остаточный член, т.е. погрешность интерполяции.

По оценке можно найти минимальное значение , гарантирующее нужную точность интерполяции. Две такие оценки следуют из приводимой теоремы.

Теорема:

Если функция непрерывна на [a,b], имеет внутри этого отрезка непрерывную , и , то для любого существует по крайней мере одна такая точка , что

Из теоремы следует:

(1) ;

(2) , где

Оценка (2) значительно грубее, но удобнее для вычисления.

Из теоремы или из оценок не следует, что интерполяционный многочлен всегда равномерно сходится к приближаемой функции.

Если для существует такое , что на отрезке , то на указанном отрезке интерполяционный многочлен равномерно сходится к рассматриваемой непрерывной функции .

П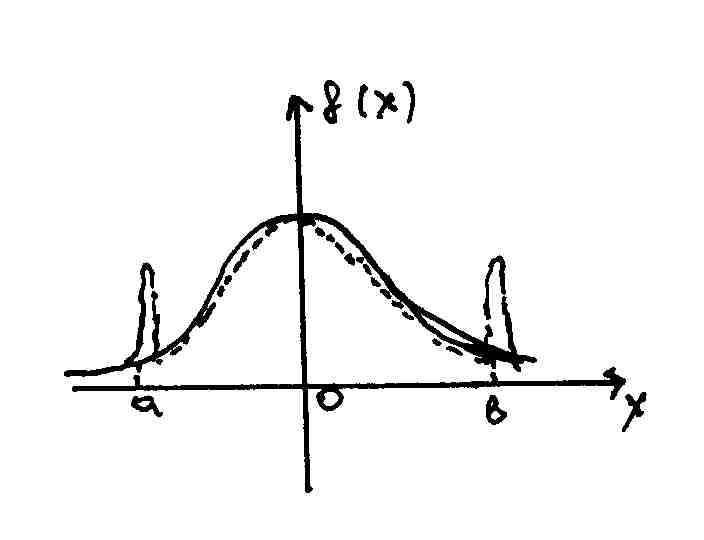 ри отсутствии равномерной сходимости на всем рассматриваемом отрезке такая сходимость многочлена к может иметь место на части этого отрезка.

Например, при x_i+1-x_i=h рассмотрим функцию .

Данная функция имеет все производные. Однако, интерп. многочлен не сходится на отрезке [a,b] при условии и .

Чтобы обеспечить сходимость ряда, можно в качестве узлов интерполир. брать узлы полиномов Чебышева для .

Для общего случая , где - узлы интерполирования полиномов Чебышева для , , . В этом случае будет иметь место равномерная сходимость. Пример:

2. Интерполяц. Формула Ньютона с пост. Шагом (для начала таблицы).

Пусть функция задана таблицей с постоянным шагом. Разности между значениями функции в соседних узлах интерполяции называют конечными разностями первого порядка:

.

Из конечных разностей первого порядка образуются конечные разности второго порядка:

Конечные разности любого порядка могут быть представлены через значения функции. Действительно, для разностей первого порядка это следует из определения. Для разностей второго порядка имеем:

.

Для разностей 3-го порядка

Методом математической индукции можно доказать, что:

Будем искать интерполяционный полином в виде:

Это полином степени n. Значение коэффициентов a₀,a₁,...,a_n найдем из условия совпадения значений исходной функции и полинома P_n(x) в узлах интерполяции. Полагая х =x₀, находим:

Далее, придавая х значение х_ и х₂ последовательно, получаем:

Найдем коэффициенты а₀, а₁, а₂:

a₀ = y₀ , ,

Аналогично можно найти и другие коэффициенты. Общая формула имеет вид:

, k=0,1,2,…,n

Подставляя эти выражения в исходную формулу, получим следующий вид интерполяционного полинома:

Полученное выражение называется интерполяционной формулой Ньютона для начала таблицы.

Если ввести новые узлы, то в данную формулу просто добавится одно слагаемое, тогда как в интерполяционной формуле Лагранжа необходим перерасчет всех коэффициентов.

Погрешность интерполяции:

, где - остаточный член, т.е. погрешность интерполяции.

По оценке можно найти минимальное значение , гарантирующее нужную точность интерполяции. Две такие оценки следуют из приводимой теоремы.