Тема 2.3. Сетевые модели

Изучается понятие и особенности сетевой модели, знакомятся с понятием сетевой график.

Практические задания: Решение задач.

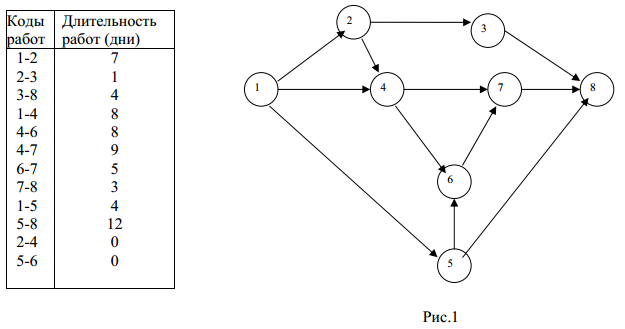
Задача 1. (критический путь)

Для заданной сетевой модели некоторого комплекса работ определить время и критический путь. 

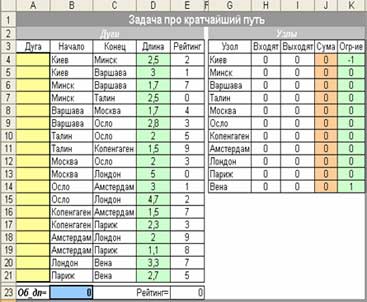
Задача 2. (кратчайший путь)

Задана сеть у виде ориентированного графа с 11 узлов и 18 дуг. Нужно найти кратчайший путь от узла-источника (Киев) к узлу-стоку (Вена). Начальные данные, ограничение и результат представим в виде двух таблиц: узлов с 11 элементов и дуг с 18 элементов.

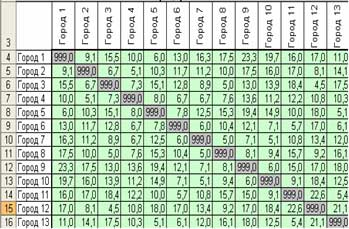
Задача 3. (Коммивояжер)

Задано полный граф из 13 городов, который описывается квадратной матрицей (13х13) расстояний между каждой парой городов. Коммивояжер должен выехать с определенного начального города (Город №1), объехать все города, побывавши в каждом городе по одному разу, и вернутся в тот же город так, чтобы общая длина была минимальной. 

Тема 2.4. Динамические модели

Изучается понятие и особенности динамической модели.

Практические задания: Решение задач.

Задача 1. Планируется деятельность четырёх предприятий на очередной год.

Начальные средства: S ₀ ус/ед. Размеры вложений в каждое предприятие кратны 1ус/ед.

Средства Х выделенные предприятию приносят в конце года прибыль F k (Х). Функции F k (Х) заданы таблично.

Принято считать, что:

• прибыль F k (Х) не зависит от вложения средств в другие предприятия;

• прибыль от каждого предприятия выражается в одних и тех же единицах;

• суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.

Задача 2. (Замена оборудования)

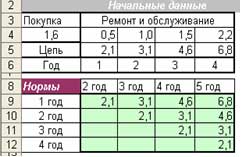
Найти такой план замены, чтобы общие затраты →min. При ограничениях: Сума по строкам первого года = 1 (Покупка в первый год); Сума по столбцам последнего года = 1 (эксплуатация до последнего года); Сума по строкам промежуточных годов = Сума про столбцам промежуточных годов; План >= 0.

Тема 2.5. Нелинейные модели

Изучается понятие и особенности нелинейной модели.

Практические задания: Решение задач.

Задача 1. (План производства)

Предприятие имеет запасы 4-х видов ресурсов (мука, жиры, сахар, финансы), с которых производится 2 виды продуктов (хлеб и батон).

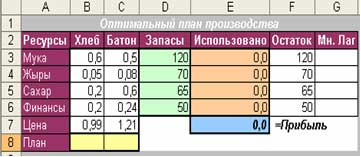
Известны:

• нормы расходов ресурсов на производство единицы продукции;

• запасы ресурсов;

• цены продуктов;

• спрос на хлеб.

Найти оптимальный план производства, при котором прибыль от реализации произведенной продукции должна быть максимальный. При чем прибыль равна выручка – затраты = цена ед. продукции * план ед. продукции – план ед. продукции^0,7

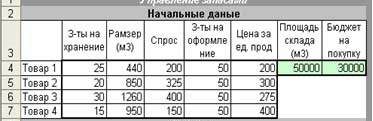
Задача 2. (Управление запасами)

Нужно определить оптимальный размер заказа четырех товаров, для каждого и них известны цены для покупки, спрос, затраты на оформление и хранение единицы продукции, а также ограничении на размер склада и суму финансирования покупки.

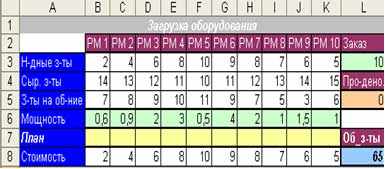
Задача 3. (Загрузка оборудования)

Заказано 10 ед. продукции, которая производится на десяти рабочих местах (машинах). Для каждой машины заданная квадратичная функция затрат на производство единицы продукции. Нужно определить оптимальный план загрузки машин, то есть, на какой машине и сколько продукции нужно произвести, чтобы выполнить заказ и при этом общие затраты были минимальными. Дополнительно могут быть заданы ограничения на: а) целочисленный план; б) максимально допустимая продуктивность машин за смену.