35). Корпускулярно-волновой дуализм. Соотношение между волновыми и корпускулярными свойствами света.

Корпускулярно-волновой дуализм – свойство любой микрочастицы обнаруживать признаки частицы (корпускулы) и волны. Наиболее ярко корпускулярно-волновой дуализм проявляется у элементарных частиц. Электрон, нейтрон, фотон в одних условиях ведут себя как хорошо локализованные в пространстве материальные объекты (частицы), двигающиеся с определёнными энергиями и импульсами по классическим траекториям, а в других – как волны, что проявляется в их способности к интерференции и дифракции. Так электромагнитная волна, рассеиваясь на свободных электронах, ведёт себя как поток отдельных частиц – фотонов, являющихся квантами электромагнитного поля (Комптона эффект), причём импульс фотона даётся формулой р = h/λ, где λ – длина электромагнитной волны, а h – постоянная Планка. Эта формула сама по себе – свидетельство дуализма. В ней слева – импульс отдельной частицы (фотона), а справа – длина волны фотона.

Дуализм электронов, которые мы привыкли считать частицами, проявляется в том, что при отражении от поверхности монокристалла наблюдается дифракционная картина, что является проявлением волновых свойств электронов. Количественная связь между корпускулярными и волновыми характеристиками электрона та же, что и для фотона: р = h/λ (р – импульс электрона, а λ – его длина волны де Бройля).

Корпускулярно-волновой дуализм лежит в основе квантовой физики.

Найдем связь между волновыми и корпускулярными характеристиками света. По формуле Планка энергия фотона равна

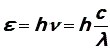
С другой стороны, по формуле Эйнштейна, выражающей эквивалентность массы и энергии, эта же энергия может быть связана с массой фотона:

Приравнивая значения энергии и выражая длину волны фотона, получим:

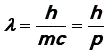(14) где p = mc – импульс фотона.

В 1924 г. Луи де Бройль (L. de Broglie) в своей диссертации “Исследования по теории квантов” предположил, что двойственная корпускулярно – волновая природа присуща не только свету, но и всем материальным частицам. Соотношение 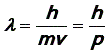(15)

аналогичное уравнению (14), где p = mv – импульс частицы, определяет длину волны любой частицы, движущейся со скоростью v. Волна, длина которой определяется уравнением (15), называется волной де Бройля. Формула (15) справедлива для любых материальных тел.

36). Спектральные серии в спектре излучения атома водорода.

Накаленные твердые тела испускают сплошные спектры. У газов (наряду со сплошной областью) наблюдаются линейчатые и полосатые спектры. Линейчатый спектр состоит из ряда закономерно расположенных более или менее узких спектральных линий. В полосатом спектре полосы кажутся сплошными при наблюдении в спектроскоп малой разрешающей силы. При применении спектрального аппарата высокой разрешающей силы они распадаются на множество тесно расположенных спектральных линий.

К началу 20-го века было выяснено, что линейчатые спектры газов испускаются атомами и ионами, а полосатые — молекулами. Поэтому их называют также атомными и молекулярными спектрами. Атомный спектр водорода удается наблюдать при электрическом разряде в вакуумной водородной трубке только тогда, когда большая часть молекул водорода диссоциировала на атомы.

Важно отметить, что каждая линия в спектре не представляет собой строго монохроматическую волну, а имеет некоторую конечную ширину.

Линии атомных спектров образуют закономерные группы, называются спектральными сериями. Промежутки между линиями в серии убывают в сторону коротких длин волн, и линии сходятся к границе серии.

Самым изученным является спектр наиболее простого атома — атома водорода.

Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:

(209.1)

где R'=1,1010⁷ м^–1 — постоянная Ридберга.* Taк как  = c/, то формула (209.1) может быть переписана для частот:

(209.2)

где R=R'c=3,2910¹⁵ с^–1 — также постоянная Ридберга.

* И. Ридберг (1854—1919) — шведский ученый, специалист в области спектроскопии.

Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями п, образуют группу или серию линий, называемую серией Бальмера. С увеличением n линии серии сближаются; значение n =  определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.

В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:

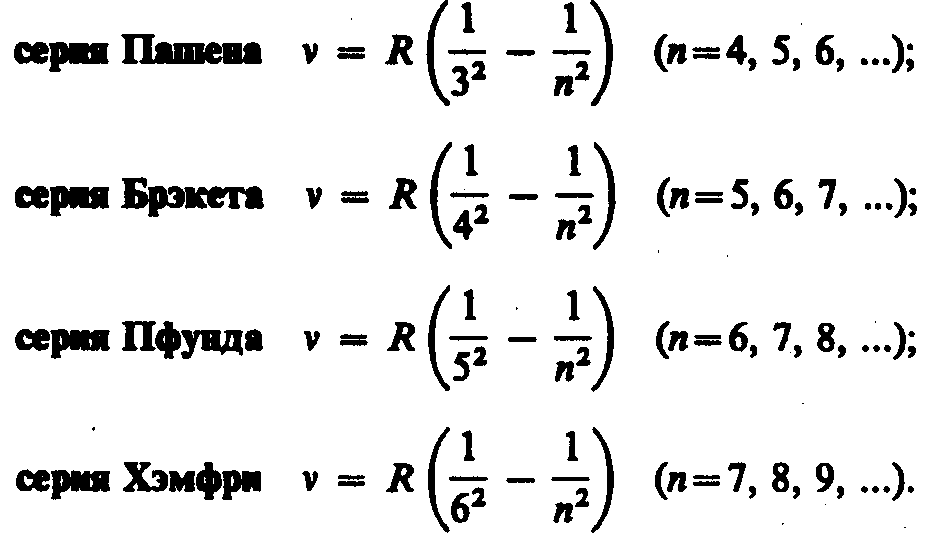
В инфракрасной области спектра были также обнаружены:

В се приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенном формулой Бальмера:

где т имеет в каждой данной серии постоянное значение, m = 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).