2.2 Примеры решения типовых задач

 

Задача 2.1 В интегродифференцирующем контуре постоянного тока (см. рисунок 2.3), применяемом для коррекции ЭЦ и САУ, определить напряжение , построить его график, если: , ,  мкФ, мкФ.        

Решение: Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало: .

Эквивалентная операторная схема после коммутации имеет вид (см. рисунок 2.4).

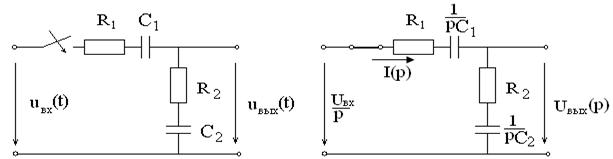
        Рисунок 2.3                                         Рисунок 2.4      

Находят изображение выходного напряжения :

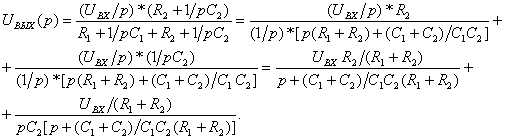                   (2.6)

         После подстановки числовых значений, получают:

                                                                          (2.7)

         Оригинал определяют по теореме разложения:

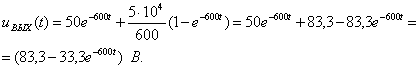
         График напряжения  построен в среде Mathcad  (см. рисунок 2.5).

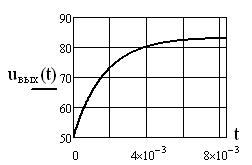
 Рисунок 2.5

 

         Задача 2.2 Электрическая цепь (см. рисунок 2.6), в которой действует источник постоянной ЭДС = , находится в установившимся режиме.        Параметры цепи: Ом, Ом, Ом, мГн, С=0,7 мкФ. В момент времени t=0 путем замыкания ключа К в цепи осуществляется коммутация. Определить ток  после замыкания ключа.

Рисунок 2.6

         Решение: 1) Определение независимых начальных условия (ННУ):  и .ННУ определяют путём расчета установившегося режима в цепи до коммутации. Установившийся режим до коммутации создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко замкнутым участком, а ёмкость размыкается (см. рисунок 2.7).

         Ток в индуктивности и напряжение на ёмкости до коммутации найдём по формулам:

А;   В.

             

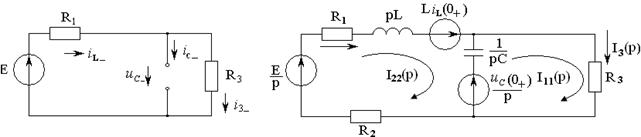
Рисунок 2.7                                                        Рисунок 2.8

 

       Независимые начальные условия определим по законам коммутации:

 

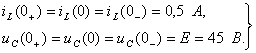                                                                     (2.8)

 

         2) Составление эквивалентной операторной схемы.

         Эквивалентная операторная схема (см. рисунок 2.8) составляется для цепи после коммутации. При составлении операторной схемы i(t), u(t), e(t) заменяют их операторными изображениями:        Индуктивность и ёмкость заменяют эквивалентными операторными схемами:

,  

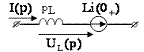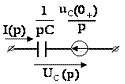
3) Определение изображения искомой величины  

         Изображение  можно определить, используя законы Ома и Кирхгофа в операторной форме, МКТ, МУП, МЭГ и т.п.

         Изображение тока проще всего определить методом контурных токов:

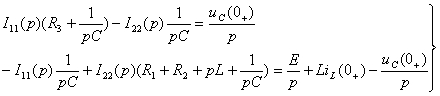                                        (2.9)

  

Из системы (2.9) находят:

 

 

= ;

 

 

.

 

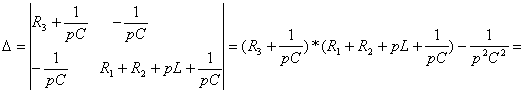
         Изображение тока  вычисляют по формуле:

                          (2.10)

 

         где

         Определяют корни характеристического уравнения 

         Корни характеристического уравнения комплексно-сопряженные, ток  находят по теореме разложения:

                       .                          (2.11)

        

         Рассчитывают:

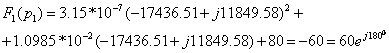
Подставляют значения  в формулу (2.11):

         Переходный ток равен:

.

 

Примечание.

         Если в рассматриваемой схеме требуется найти напряжение на ёмкости , то для определения изображения  более рационально применить метод двух узлов.

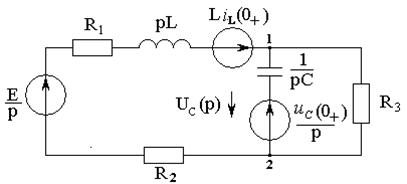
                                                        Рисунок 2.9

 

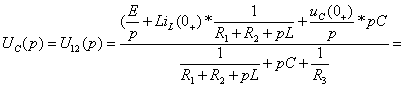
                                                                   (2.12)

 

 

Задача 2.3 Электрическая цепь (см. рисунок 2.10) содержит источник синусоидальный ЭДС , резистивные сопротивления, индуктивность, емкость и находится в установившимся режиме. В момент времени  в цепи происходит коммутация (ключ замыкается). Определить ток  после коммутации.

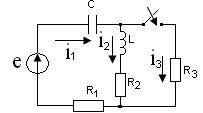
Рисунок 2.10

         Значения ЭДС и параметров цепи: В, ,   , Ом, Ом, Ом.

Решение: При расчёте переходных процессов в электрической цепи с синусоидальным источником ЭДС операторным методом целесообразно применить метод наложения: принужденные токи и напряжения определяются путем расчёта установившихся режимов в цепи после коммутации комплексным методом (как в классическом методе), а свободные токи и напряжения определяются операторным методом.

1) Определяют независимые начальные условий (ННУ): , .

         Независимые начальные условия определяются путём расчёта установившегося режима в цепи до коммутации. Установившийся режим до коммутации создаётся источником синусоидальной ЭДС и при расчёте применяется комплексный метод (см. рисунок 2.11).

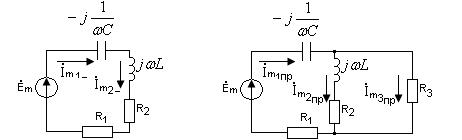
                          Рисунок 2.11                                      Рисунок 2.12

 

         Комплексная амплитуда ЭДС: ;

         Индуктивное и ёмкостное сопротивления: Ом;

Ом;

         Комплексное сопротивление всей цепи до коммутации равно: Ом .

         Комплексную амплитуду тока  и напряжение  определяют по закону Ома.

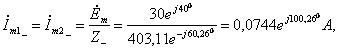                                                     (2.13)

                                  (2.14)

         Записывают мгновенные значения тока на индуктивности и напряжения на ёмкости до коммутации:

;      .

         Определяют значения тока на индуктивности  и напряжение на ёмкости в момент

(4)

 

         Независимые начальные условия ,  определим по законам коммутации:

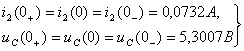                                                                               (2.15)

2) Рассчитывают установившийся режим в цепи после коммутации, создаваемый  источником синусоидальной ЭДС В, комплексным методом (см. рисунок 2.12).Определяют принужденный ток , а также принужденного тока в индуктивности  и принуждённого напряжения на ёмкости .

         Комплексная амплитуда ЭДС: =22,98+19,84 В.

         Комплексное входное сопротивление цепи после коммутации, токи  и напряжение  равны:

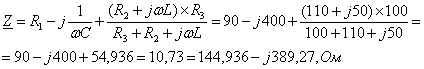                                  (2.16)

                                                  (2.17)

                                     (2.18)

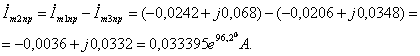                                    (2.19)

                                             (2.20)

         Мгновенные принуждённые токи , и мгновенное напряжение    соответственно равны:

                                                                          (2.21)

                     (2.22)

                                                                                      (2.23)

3) Определение свободного тока .

         Свободный ток  определяют операторным методом.

         а) Составляют эквивалентную операторную схему для определения , которая содержит только внутренние (расчётные ) ЭДС:    и не содержит изображение внешнего источника ЭДС . Направление ЭДС  совпадает с направлением тока в ветви, направление ЭДС  противоположно направлению тока в ветви.         Эквивалентная операторная схема представлена на рисунке 2.13.

                                     

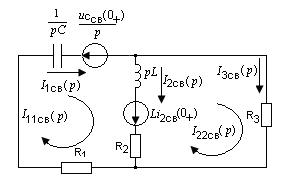
Рисунок 2.13

 

         Находят и :

,

         где  

 

         б) Определение изображения. .

         По эквивалентной операторной схеме (см. рисунок 2.13) определяют изображение тока , используя метод контурных токов:

 

 

         Из системы контурных уравнений находят изображение :

     =

 

 

             =

 

 

                                                                                                      

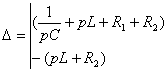
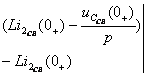                               (2.24)

 

         где

 

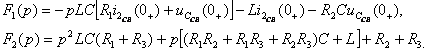
         в) Определение свободного тока  по его изображению .       Вычисляют корни характеристического уравнения :

 

                                                                            (2.25)

         Корни характеристического уравнения комплексно сопряжённые:

 

         Свободный ток  находят по теореме разложения:

 

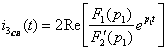                                                 .                                        (2.26)

 

         Вычисляют: , , :

 

 

 

 

         Подставляют , в формулу (2.26) и вычисляют :

         Переходный ток записывают в виде