Задачи на условный экстремум. Метод множителей Лагранжа. Необходимое условие существования условного локального экстремума функции

Пусть и , — дважды непрерывно дифференцируемые скалярные функции векторного аргумента . Требуется найти экстремум функции при условии, что аргумент удовлетворяет системе ограничений: , (последнее условие называют также условием связи).

Наиболее простым методом нахождения условного экстремума является сведение задачи к нахождению безусловного экстремума путем разрешения уравнения связи относительно s переменных и последующей их подстановки в целевую функцию.

В более сложных случаях выразить переменные удается не всегда. Соответственно, описанный выше подход применим не ко всем задачам. Более универсальным методом решения задач отыскания условного экстремума является метод множителей Лагранжа. Он основан на применении следующей теоремы. Если точка является точкой экстремума функции в области, определяемой уравнениями , , то (при некоторых дополнительных условиях) существует такой s-мерный вектор , что точка является стационарной точкой функции:

Алгоритм метода множителей Лагранжа

1 . Составить функцию Лагранжа:

где — множитель Лагранжа, соответствующий i-му ограничению.

2. Найти частные производные функции Лагранжа и приравнять их к нулю

3. Решив получившуюся систему из n + s уравнений, найти стационарные точки.

Заметим, что в стационарных точках выполняется необходимое, но не достаточное условие экстремума функции. Анализ стационарной точки на наличие в ней экстремума в данном случае достаточно сложен. Поэтому метод множителей Лагранжа в основном используют в тех случаях, когда о существовании минимума или максимума исследуемой функции заранее известно из геометрических или содержательных соображений.

При решении некоторых экономических задач множители Лагранжа имеют определенное смысловое содержание. Так, если — прибыль предприятия при плане производства n товаров , — издержки i-го ресурса, то — оценка этого ресурса, характеризующая скорость изменения оптимума целевой функции в зависимости от изменения i-го ресурса.

Необходимые условия существования локальных экстремумов

Из леммы Ферма вытекает следующее:

Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .

Тогда либо производная не существует, либо .

Задача выпуклого программирования. Теорема Куна-Таккера

В теории выпуклого программирования в качестве основной рассматривается задача минимизации выпуклой функции  (1.1) при условиях   (1.2)  (1.3) где функции   предполагаются выпуклыми. Если   и   являются вогнутыми функциями, то имеем задачу максимизации   при ограничениях   и  [5] Составим функцию Лагранжа для данной задачи: 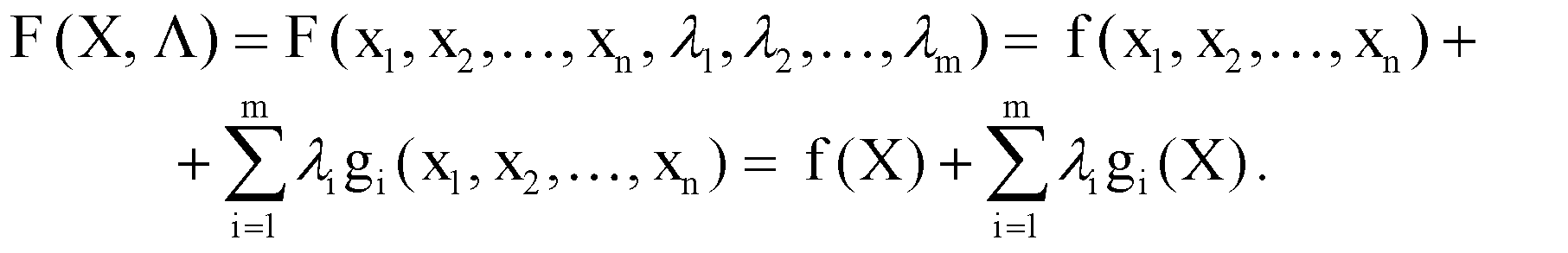 (1.4) Точка   называется седловой точкой функции (1.4), если точка   является точкой минимума функции  , а точка   - точкой максимума функции  . Другими словами, для седловой точки при всех   и   выполняется соотношение  (1.5) Теорема Куна-таккера. Пусть существует по крайней мере одна точка  , для которой  . Тогда необходимым и достаточным условием оптимальности вектора  , принадлежащего области допустимых решений задачи (1.1)-(1.5), является существование такого вектора  , что для всех   и   имеют место неравенства (1.5). Теорема Куна-Таккера также называется теоремой о седловой точке.