Сущность процесса моделирования:

I Выбор объекта исследования. Построение модели. Вопрос о необходимой и достаточной мере сходства объекта оригинала и его модели. Изучение одних сторон моделируемого объекта осуществляется ценой отказа от изучения других сторон. Любая модель замещает объект лишь в строго ограниченном смысле. Результатом первого этапа является создание модели.

II изучение модели. Сама модель выступает объектом исследования – проведение модельных экспериментов при изменяющихся внешних условиях функционирования. Знания систематизируются и в результате мы получаем систему знаний о модели.

III перенос знаний – знания переносятся по принципу адекватность / неадекватность модели исследуемому объекту - результат переноса необходимо связан с признаками модели и объекта оригинала. В результате мы получаем систему знаний об объекте.

IV проверка и применение. Практическая проверка полученных с помощью модели знаний . практическая проверка направлена на построение обобщающей теории объекта, его преобразование и управление ним.

В методологии моделирования заложена возможность саморазвития т.к. это многоэтапный процесс.

№5. Линейное программирование. Предмет. Характерные особенности линейного программирования.

Первые постановки задач линейного программирования были сформулированы известным советским математиком Л.В.Канторовичем, которому за эти пионерские работы была присуждена Нобелевская премия по экономике. Значительное развитие теория и алгоритмический аппарат линейного программирования получили с изобретением и распространением ЭВМ и формулировкой американским математиком Дж. Данцингом симплекс-метода В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений.

Суть - сформировать допустимое множество решений->найти наиболее подходящее решение; все задается линейно.

Предмет – вычисление экстремума линейной функции при условии, что все переменные, подлежащие определению, удовлетворяют линейным ограничениям.

Процесс построения модели ЗЛП условно можно разбить на  этапы:

1.выбор объекта исследования и идентификация переменных;

2.определение цели исследования;

3.определение критерия оптимальности и записи его в формализованном виде как целевую функцию модели ЛП;

4.выявление и построение основных ограничений задач, позволяющих сформировать множество допустимых вариантов.

№6. Структура общей задачи линейного программирования. Допустимые и оптимальные решения задачи.

Дана система m линейных уравнений и неравенств с n переменными.

a 11x1+a12x2+…+a1nxn< либо =b1

a12x2+a22x2+…+a2nxn<либо <=b2

………………………………………

ak1x1+ak2x2+….+aknxn<либо=bk

ak1+1,1x1+ak1+1,2x2+…+ak+1nxn=bk+1,

ak+2,1x1+ak2,2x2+…+ak+2nxn = bk+2,

…………………………………………..

am1x1+am2x2+…+amnxn=bm.

И линейная функция : F=c1x1+c2x2+…+cnxn

Необходимо найти такое решение системы X=(x1,x2…,xj…,xn),

где xj>=0 (j=1,2,…,L; L<=n)

при котором линейная функция F принимает оптимальное значение (то есть максимальное или минимальное значение).

Система называется системой ограничений, а функция – линейной функцией. Более кратко задачу линейного программирования можно представить в виде:

∑ cjxj  max ( или min)

Допустимые решения задачи ЛП - множество решений, одновременно удовлетворяющих все ограничения модели.

Оптимальным решением задачи линейного программирования называется решение системы ограничений, удовлетворяющее условиям, при которых линейная функция принимает оптимальное значение.

№7. Область определения задачи линейного программирования. Зависимость между областью определения задачи линейного программирования и ее решением.

Теорема 1.

Область определения задачи ЛП представляет собой замкнутое выпуклое множество.

Множество называется замкнутым, если ему принадлежат все граничные точки.

Множество называется выпуклым, если ему вместе с двумя произвольными точками принадлежит и отрезок их соединяющий.

Угловые точки-вершины области допустимых значений.

Теорема 2.

Целевая функция задачи ЛП всегда достигает своего экстремального значения в угловой точке многогранника допустимых решений. Если целевая функция достигает экстремального значения более чем в одной угловой точке, то она достигает того же значения в любой точке соединяющего их отрезка.

Область допустимых решений задачи ЛП может быть:

1.замкнутым ограниченным множеством; задача имеет либо одно, либо бесконечное множество оптимальных решений;

2.замкнутым неограниченным множеством; задача имеет либо одно, либо бесконечное множество оптимальных решений, либо не имеет оптимальных решений в силу неограниченности множества;

3.пустым; задача не имеет оптимальных решений.

№8. Задача об использовании ресурсов(об ассортименте продукции). Ее модель.

Небольшая фабрика выпускает два вида красок; краску для наружных(1) и внутренних(2) отделочных работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используется два исходных ресурса. Ресурс А и Б. Расходы исходных ресурсов А и Б на изготовление 1т краски представлены в таблице:

Исходные ресурсы	Расход исходных ресурсов в тоннах на производство 1т краски		Max возможный суточный запас исходных ресурсов,т
	Краски 1,т	Краски 2,т
А	1	2	6
Б	2	1	8

Изучение рынка сбыта показало, что суточный спрос на кр.2 никогда не превышает суточный спрос на кр.1 более чем на 1т. Также спрос на кр.2 никогда не превышает 2т в сутки. Оптовые цены 1т краски составляют:$3000-кр.1-1т; $2000-кр.2-1т.

Какое количество краски каждого вида должна производить фабрика с тем, чтобы доход от реализации продукции был максимальным.

Объект исследования: планирование объемов выпуска краски каждого вида с использованием ограниченных ресурсов А и Б. Х1-суточный выпуск краски 1; Х2-2.

Цель: составление плана выпуска продукции, приносящего фабрике максимальный доход.

Критерий оптимальности: максимизация дохода от реализации.

3х1+2х2-max

Ограничения задачи:

Х1+2х2<=6

2х1+х2<=8

х2<=2

х2-х1<=1

х1>=0 x2>=0

№9. Задача о диете. Ее модель.

Бройлерное хозяйство птицеводческой фермы насчитывает 20 тыс цыплят, которые выращиваются до восьминедельного возраста и после соответствующей обработки поступают в продажу. Каждый цыпленок за 8 недель должен съесть 1 фунт корма(445гр). Для того, чтобы цыплята достигли необходимых весовых кондиций кормовой рацион должен удовлетворять определенным требованиям по питательности. Корм: известняк, зерно, соевые бобы. Требования по питательности должны соответствовать 3-м видам питательных веществ: кальций, белок, клетчатка.

Содержание питательных веществ в каждом из ингредиентов корма.

ингредиенты	Содержание питательных веществ в фунтах на фунт ингредиента			Стоимость в $ за фунт
	Кальций	Белок	Клетчатка
Известняк	0.38	-	-	0.04
Зерно	0.001	0.09	0.02	0.15
Соевые бобы	0.002	0.5	0.08	0.4

Кормовая смесь должна содержать не менее 0.8% но не более 1.2% кальция; не менее 22% белка; не более 5% клетчатки. Составить смесь для кормления цыплят, удовлетворяющую требованиям по клетчатке с минимальными затратами на приобретение ингредиентов.

Объект исследования: составление смеси для кормления цыплят, удовлетворяющую требованиям по питательности.

Х1-содержание известняка в фунтах в смеси;Х2-зерна;Х3-соевых бобов.

Цель: составление смеси, удовлетворяющей требованиям питательности с минимальными затратами на приобретение ингредиентов.

Критерий оптимальности: минимизация затрат на покупку ингредиентов.

0.04х1+0.15х2+0.4х3-min

Ограничения задачи:

x1+х2+х3>=20000

0.372x1-0.007x2-0.006x3>=0

0.368x1-0.011x2-0.01x3<=0

0.22x1+0.13x2-0.28x3<=0

0.05x1+0.03x2=0.03x3>=0

x1>0 x2>0 x3>0

№10. Задача о раскрое или минимизации обрезков. Ее модель.

Продукция бумажной фабрики выпускается в виде бумажных рулонов стандартной ширины 20м. По специальным заказам фабрика поставляет рулоны и других размеров, для чего производится разрезание рулонов стандартной ширины. Типичные заказы на нестандартные рулоны:5,7,9м. Фирме поступил заказ на рулоны нестандартных размеров:5м-150 заказов;7м-200з;9м-300з. Требуется найти сочетание вариантов установки режущей кромки, при которой поступившие заказы на нестандартные рулоны будут удовлетворены с минимальными потерями.

Объект: сочетание вариантов установки режущей кромки для выполнения заказов на нестандартные рулоны.

Требуемая ширина рулона	Вариант установки режущей кромки
	1	2	3	4	5	6
5	4	2	2	1	-	0
7	-	1	0	2	-	1
9	-	-	1	-	2	1
Потери	0	3	1	1	2	4

Х1-количество рулонов, разрезанных по 1-му варианту;Х2-по 2-му;Х3-по3-му;Х4-по 4-му;Х5-по 5-му;Х6-по 6-му.

Цель: найти сочетание вариантов установки режущей кромки для выполнения заказов при минимальных потерях.

Критерий оптимальности: минимизация обрезков.

(3х2+х3+х4+2х5+4х6+5у1+7у2+9у3)*l-min

У1-колчество лишних рулонов шириной 5м

У2-7м

У3-9м

l-длина рулонов

Ограничения задачи:

4х1+2х2+2х3+4х4-у1=150

х2+2х4+х6-у2=200

х3+2х5+х6-у3=300

Xi>=0 (i=1,6)

Yj>=0 (j=1,3)

№11. Задача о сменно-суточном планировании работы автобусного парка. Ее модель.

Исследуются возможности более рационального использования городского транспорта с целью снижения интенсивности внутригородского движения.

0-44 авт; 4-8 8 авт; 8-12 10авт; 12-16 7 авт; 16-2012 авт; 20-24 4 авт.

Было решено, что с учетом необходимых затрат времени на текущий ремонт и обслуживание, непрерывное использование автобуса на линии должно быть 8 часов. Определить расписание и количество автобусов в каждой из смен, при котором будет удовлетворена потребность в перевозках, при условии, что общее количество автобусов в течение всей работы минимально.

Объект: составление расписания автобусов, выходящих на линии города в сутки, с условием удовлетворения потребностей в перевозке.

Цель: составление расписания, при котором количество автобусов на линии в течение суток будет минимальным.

Х – количество автобусов в смену.(6 смен)

Критерий оптимальности: минимизация количества автобусов на линии в течение суток.

Х1+Х2+Х3+Х4+Х5+Х6min

Ограничения:

Х1+Х6>=4

X1+X2>=8

X2+X3>=10

X3+X4>=7

X4+X5>=12

X5+X6>=4

Xi>=0 (i-1,6)

№12. Графический метод решения задач линейного программирования.

1 шаг - геометрическое представление множества допустимых решений задачи, в котором одновременно выполняются все ограничения модели.

2 шаг – нахождение оптимального решения.

Вектор «С» задает направление возрастания целевой функции задачи и строится по коэффициентам целевой функции(выходит из (0,0)). Графически увеличение целевой функции задачи соответствует параллельному сдвигу вектора «Х» в направлении заданном вектором «С». Полученные положения вектора «Х» называются линиями уровня. Особенность линии уровня состоит в том, что целевая функция на ней принимает одинаковые значения(то есть, координаты любой точки подставляем в целевую функцию и получаем одинаковые значения). Чем выше линия, тем больше значение. Последняя точка соприкосновения самой высокой линии уровня с областью допустимых решений задачи и дает нам оптимальное решение задачи.

№13. Первая задача анализа на чувствительность. Дефицитный и недефицитный ресурсы.

Позволяет ответить на вопрос: на сколько можно сократить или увеличить запасы исходных ресурсов; при этом необходимо проанализировать следующие 2 аспекта:

1. на сколько можно увеличить запас некоторого исходного ресурса с тем, чтобы улучшить полученные раннее оптимальные решения задачи.

2. на сколько можно снизить запас некоторого исходного ресурса, при сохранении полученного раннее оптимального решения задачи.

1-ая задача анализа на чувствительность носит название анализ на чувствительность к правой части ограничения.

Первоначально необходимо классифицировать ограничения задачи на связывающие (активные) и несвязывающие (пассивные). Прямая, представляющая связывающие ограничения должна проходить через оптимальную точку. В противном случае ограничение будет несвязывающим. После классификации ограничений проводят классификацию исходных ресурсов. Если ограничение является связывающим, то соответствующий ему ресурс относится к разряду дефицитных ресурсов (и наоборот, несвязывающее ограничение – недефицитный ресурс). Дефицитный ресурс – это ресурс, который используется полностью. Недефицитные ресурсы – ресурсы, находящиеся в некотором излишке.

Теперь можем изменить или модернизировать аспекты задачи анализа на чувствительность:

1 аспект: на сколько можно увеличить запас некоторого дефицитного ресурса с тем, чтобы улучшить полученные раннее оптимальные решения задачи.

2 аспект: на сколько можно снизить запас некоторого недефицитного ресурса с тем, чтобы найденные раннее неоптимальные решения не изменились.

№14. вторая задача анализа на чувствительность

Отвечает на вопрос: увеличение какого из ресурсов наиболее выгодно.

Для ответа на этот вопрос вводятся дополнительные переменные, обозначающие характеристику ценностей каждой дополнительной единицы дефицитного ресурса (yi (игрек i-ое)).

Max приращение целевой функции задачи

yi= -------------------------------------------------------------------------------

Max допустимый прирост объёма i-ого дефицитного ресурса

Данные Max приращение целевой функции задачи и Max допустимый прирост объёма i-ого дефицитного ресурса берутся из первой задачи анализа на чувствительность. Считаем yi для каждого дефицитного продукт. И делаем след вывод: увеличение дефицитного продукта 1 на 1 ед чего-то (смотря что в задаче, тонны или кг) приводит увеличение целевой функции на y1 (то, что нашли по формуле).

В результате проведения 2-ой задачи, можно сделать вывод:

Чем больше характеристика ценностей каждой дополнительной единицы ресурса, тем более эффективным является увеличение данного ресурса.

Смотрим у какого дефицитного продукта показатель yi больше, следовательно его и надо увеличивать.

№15. 3-я задача анализа на чувствительность.

Вопрос: в каких пределах допустимо изменение коэффициентов целевой функции задачи.

Имеет 2 аспекта

1-ый аспект: каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменение оптимального решения.

2-ой аспект: на сколько следует изменить тот или иной коэффициент целевой функции с тем, чтобы изменилось оптимальное решение и статус ресурсов, т.е. некоторый недефицитный ресурс стал дефицитным и наоборот.

1-ый аспект

Общий вид целевой функции C1∙x1+C2∙x2->min/max

Изменение коэффициентов в целевой функции оказывает влияние на положение вектора С и перпендикуляра к нему, который представляет целевую функцию. Т.е изменение коэффициента в целевой функции изменяет линию наклона целевой функции.

Пусть const=C1, а С2-изменяем. Если С2 увеличиваем – увеличение С2 соответствует развороту линии уровня против часовой стрелки. Уменьшение С2- разворот по часовой.

Пусть const=С2, увеличение С1- изменение по часовой стрелке. И делаем вывод:

При стабильном и неизменном С1 равным …, какое бы значение не принимал С2 в диапазоне от … до …. Включительно, точка Е (точка оптимального решения задачи) по прежнему останется оптимальным решением и следовательно статус ресурса останется неизменным.

2-ой аспект

Как только значения коэффициентов целевой функции выйдут за диапазон, указанный в 1-ом аспекте 3-ей задачи на чувствительность, оптимальное решение задачи изменится и автоматически изменится статус ресурсов.

№16. Симплекс-метод. Решение задач линейного программирования с использованием Excel.

В Excel существуют дополнительные возможности, которые представлены надстройками. Надстройки – это особое приложение, способное расширить основные возможности Excel. Наиболее часто используемые в бизнесе и управлении надстройки, это – «пакет анализов» и «поиск решения». Пакет анализа – это надстройка, котроая представляет собой набор программ по статистической обработке данных и прогнозированию. Поиск решения – предназначена для оптимизации линейных и нелинейных моделей. Любую надстройку необходимо активировать. Excel – сервис – надстройки – поиск решения. Дальше вбиваем туда всю информацию – целевая ячейка, максимум или минимум, какие ячейки изменяем и все ограничения. Когда закончили – ок. Дальше: параметры – параметры поиска решений – и выделяем галочкой линейная модель, неотрицательные решения, автоматическое масштабирование. И нажимаем на Поиск решения. Результаты поиска решения – решения найдены, все условия выполнены – сохранить решение – тип отчёта: результаты, устойчивость, пределы.

№17 Классическая постановка транспортной задачи (дальше - ТЗ). Модели транспортной задачи.

Имеется m поставщиков однородного груза. Каждый поставщик обозначается a; А_i – объем груза; n – число потребителей; b_j - потребитель. Стоимость перевозки единицы груза от i-ого поставщика к j-ому потребителю – транспортный тариф, c_ij. Необходимо составить такой план перевозки груза, при котором будут минимальные транспортные издержки.

Транспортная таблица:

	b1	B2	…	bn
a2
a1
…
am

Строка верхняя b₁ … b_{n –} потребность в грузе данного потребителя.

Левый столбец а₁ … а_{n –} наличие груза у данного поставщика.

Модель ТЗ

1) Объект исследования – составление плана перевозки груза.

x_ij – количество груза, перевозимого от i-ого поставщика к j-ому потребителю.

2) Цель исследования – составить такой план перевозки груза, при котором издержки будут минимальными.

3) Критерий оптимальности: минимизация транспортных издержек.

№18 Сбалансированная и несбалансированная модели транспортной задачи.

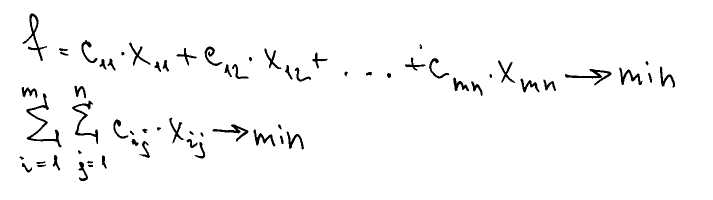
Приведение открытой модели транспортной задачи к закрытой. Метод запрещения перевозок.

(продолженение предыдущего вопроса и одновременно следующий)

При постановке конкретных задач перевозки грузов может возникнуть одна из задач:

a) сумма количества груза у всех поставщиков равна сумме потребности в грузе всех потребителей.

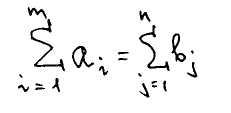
b) общее количество груза у всех поставщиков больше суммы потребности в грузе всех потребителей.

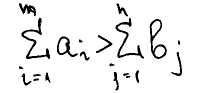
c) общее количество груза у всех поставщиков меньше суммы потребности в грузе всех потребителей.

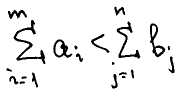
Каждой ситуации соответствует определенная модель ограничений ТЗ. Бывают ограничения по потребителям и по поставщикам.

Для первой ситуации:

Весь груз, который есть у поставщика, будет вывезен.

Такая модель ТЗ называется ЗАКРЫТОЙ моделью, а задача, ей соответствующая – СБАЛАНСИРОВАННОЙ.

Для второй ситуации:

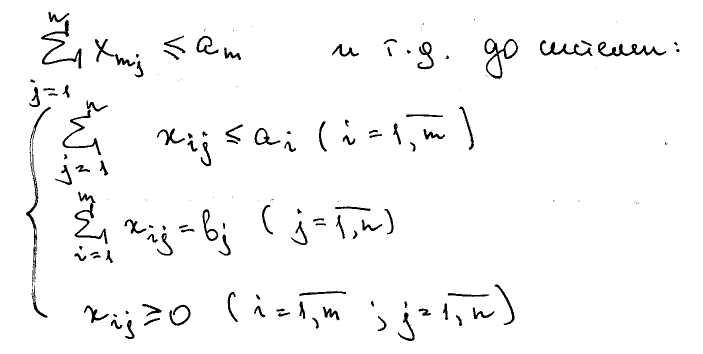
Для третьей ситуации:

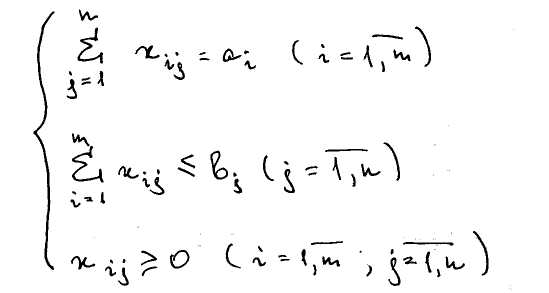
Такие как 2-ая и 3-я модели ТЗ называются ОТКРЫТЫМИ МОДЕЛЯМИ ТЗ, а соответствующие им задачи – НЕСБАЛАНСИРОВАННЫМИ.

Разрешимой является только сбалансированная задача. Для того, чтобы модели, соответствующие 2-ой и 3-ей ситуации были разрешимыми, задачи необходимо привести к закрытому сбалансированному виду.