Создать процедуру, позволяющую вычислять коэффициенты разложения в ряд Тейлора и старший член погрешности.
Вычислить отрезок ряда Тейлора с точностью
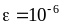
Найти точное решение задачи (1) и составить процедуру его вычисления. Если возможно, с помощью пакета, выполняющего символьные преобразования, вычислить его разложение в ряд Тейлора.
Вычислить отрезок ряда Тейлора с точностью в случае, когда в начальные условия внесена случайная ошибка.
Сравнить полученные разложения, вычислив значения погрешности приближенного решения в точках
,
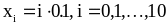либо вычислив погрешности коэффициентов.Вариант 2.
Предлагается задача Коши
,
.
(1)
Требуется:
Создать программу, реализующую алгоритм метода Predictor–Corrector, использующий методы Адамса третьего порядка. Число итераций t считать фиксированным (t=3).
Вычислить приближенное решение
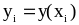задачи (1) в точках
,
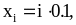
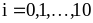с точностью
.
Шаг
для расчета положить равным
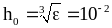.Найти точное решение задачи (1).
Проанализировать результат расчета, вычислив соответствующие погрешности
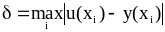.Вариант 3.
Предлагается задача Коши
,
.
(1)
Требуется:
Создать программу, реализующую алгоритм вложенного метода Рунге – Кутты – Фельдберга с автоматическим выбором. Расчет одного шага метода RKF 2(3) выполняется по формулам
,
,
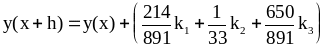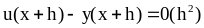
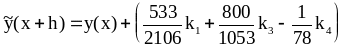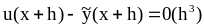
где
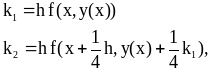
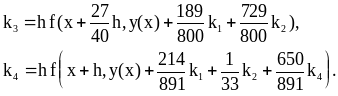
Вычислить приближенное решение задачи (1) в точках , с точностью .
Найти точное решение задачи (1).
Проанализировать результат расчета, вычислив соответствующие погрешности .
Задание №2.
Тема: Решение задачи Коши для уравнения первого порядка с параметром.
На примере задачи Коши для уравнения с параметром
,
(1)
сравнить качество (реальную погрешность вычисленного решения и время расчета ) выбранного метода (или методов) приближенного решения задачи Коши.
В варианте задания желательно, чтобы при одном значении параметра задача была устойчивой относительно ошибок округления, а при другом неустойчивой
Примеры вариантов задания
Вариант 1.
Предлагается задача Коши
,
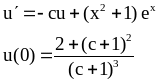, (1)
для значений
параметра
и
.
Требуется:
Найти точное решение задачи (1).
Вычислить приближенное решение
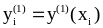задачи (1) в точках
,
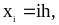h=0.1
с
точностью
,
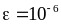используя метод Эйлера с автоматическим
выбором шага.Вычислить приближенное решение
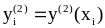задачи
(1) в точках
,
h=0.1
с
точностью
,
используя метод Рунге- Кутты порядка
не менее третьего с автоматическим
выбором шага.Сравнить используемые методы, вычислив соответствующие погрешности
,
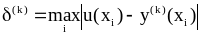k=1,2, и
количество вычислений правых частей
задачи (1), необходимых для получения
заданной точности.
Вариант 2
Предлагается задача Коши
,
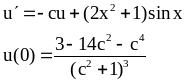, (1).
для значений
параметра
и
.
Требуется:
Создать программы, реализующие алгоритм метода Рунге – Кутты с автоматическим выбором шага и разностного метода с постоянным шагом
.
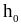Методы должны быть порядк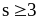а
,
а
.
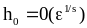Можно также использовать доступные
Вам стандартные программы выбранных
методов.Вычислить приближенное решение задачи (1) в точках , с точностью , используя разностный метод.
Вычислить приближенное решение задачи (1) в точках , с точностью , используя метод Рунге- Кутты.
Найти точное решение задачи (1).
Сравнить используемые методы, вычислив соответствующие погрешности , k=1,2, и количество вычислений правых частей задачи (1), необходимых для получения заданной точности.
Задание №3.
Тема : Решение задачи Коши для уравнений p–ого порядка
методами Рунге — Кутты.
Предлагается найти приближенное решение задачи Коши для уравнения
,
(1)
используя метод Рунге – Кутты, и сравнить с точным решением, которое задается в варианте задания. Результаты представить в виде таблицы или графиков.
Варианты для этого задания аналогичны предыдущим.
Литература.
Бахвалов Н.С. Численные методы.–М.:Наука.1975.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы.–М.:Наука.1987.
Калиткин Н.Н. Численные методы.–М.:Наука.1978.
Самарский А.А., Гулин А.В. Численные методы.–М.:Наука.1989.
Дж. Ортега, У. Пул Введение в численные методы решения дифференциальных уравнений.–М.:Наука.1989.
Современные численные методы решения обыкновенных дифференциальных уравнений, редакторы Дж Холл и Дж Уатт.–М.:Мир.1979.
Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях.–М.: Высшая школа.2000.