28

Министерство Образования Российской Федерации

Ростовский государственный университет

С. Н. ОВЧИННИКОВА

Методические указания

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ

ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

(для студентов 3 и 4 курсов мехмата)

Ростов–на–Дону

2001г.

Современная вычислительная техника позволяет приближенно находить решения больших и сложных задач Коши. Особую важность при таких расчетах имеет гарантированная точность вычисленного решения. Она зависит от точности используемой ЭВМ, а также от устойчивости численного метода и реализующего его алгоритма.

Существуют мощные пакеты программ, предназначенные как для численного, так и для символьного решения обыкновенных дифференциальных уравнений (ОДУ). Уверенному использованию таких пакетов помогают знания вычислительных методов решения ОДУ и их особенностей. Встречаются также задачи, для которых нужно модифицировать старые или создать новые методы и алгоритмы.

В данных методических указаниях рассматриваются несколько наиболее распространенных методов решения нежестких задач Коши, предлагаются упражнения, требующие небольших ручных или компьютерных вычислений, а также задания для курса “Практикум на ЭВМ”. Все задания содержат упрощенные задачи с известными решениями, что позволяет оценить эффективность рассматриваемых методов. Заметим, что задачи с известным решением полезны при различных расчетах как контрольные варианты для более сложных вычислений.

Для выполнения заданий удобен математический пакет Maple, однако можно использовать любой язык программирования, а также стандартные программы, реализующие выбранные методы.

Подавляющее большинство методов и алгоритмов применяются для решения систем обыкновенных дифференциальных уравнений первого порядка. Это объясняется тем, что дифференциальное уравнение любого порядка можно свести к эквивалентной системе ОДУ первого порядка. Как проще всего это сделать, покажем на примере задачи для обыкновенного дифференциального уравнения p-ого порядка, разрешенного относительно старшей производной,

, (1)

с начальными условиями

. (2)

Замена

,

позволяет записать (1) в виде системы ОДУ первого порядка

Теперь задача Коши (1)–(2) эквивалентна векторному уравнению

(3)

,

где вектор – функции и имеют размерность р. Аналогично систему дифференциальных уравнений любого порядка можно заменить эквивалентной системой уравнений первого порядка и не одним способом.

Многие вычислительные методы для задачи (3) можно получить, обобщая методы решения задачи Коши для одного уравнения. Суть такого обобщения состоит в переходе от скалярных равенств и выражений к векторным. Поэтому обычно рассматриваются вычислительные методы на примере решения задачи Коши для уравнения первого порядка

. (4)

Далее предполагается, что выполнены условия теоремы существования и единственности решения задачи Коши, причем решение имеет достаточное число непрерывных производных.

Разложение решения в ряд Тейлора.

Такой метод нахождения приближенного решения применяется тогда, когда есть возможность вычислять нужное число производных правой части системы (4) вручную или с помощью пакета программ, выполняющих символьные преобразования (например, с помощью пакета Maple).

Пусть задача (4) имеет решение u(x), у которого существует достаточное число непрерывных производных на . Тогда u(x) можно разложить в ряд Тейлора в окрестности точки

где .

Коэффициенты этого разложения легко вычислить, если известны значения u(x) и ее производных в точке . Значения первых коэффициентов и заданы в постановке задачи. Вручную или с помощью пакета, позволяющего выполнять математические операции на ЭВМ, можно найти следующие k производных

,

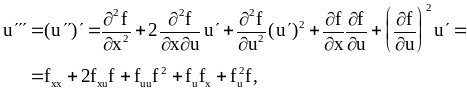
и так далее. Вычислив их значения в точке , получим приближенное решение

,

и главный член погрешности

.

Если известен радиус сходимости r ряда Тейлора, и , то при некотором значении k отрезок ряда приближает точное решение с заданной точностью. Если же , то разбивается на отрезки такие, что . На каждом отрезке вычисляется с заданной точностью приближенное решение

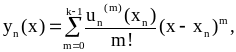
где , – рассчитанное на предыдущем отрезке решение.

Ошибка приближенного решения на имеет порядок . К последнему отрезку, как правило, накопится ошибка, и погрешность будет иметь порядок , если .

При практическом счете контроль сходимости можно заменить условием , –точность расчета. Если это условие не выполняется для выбранного числа k, то надо либо уменьшить шаг h либо увеличить k. Очевидно, значение k не должно быть очень большим, а шаг h очень малым. Большое число слагаемых k в разложении означает высокие требования к гладкости решения и трудности использования такого разложения. Очень малый шаг h соответствует плохой сходимости, то есть предположение о порядке гладкости решения, по-видимому, было неверным.

Алгоритм вычисления отрезка ряда Тейлора для

решения задачи Коши с помощью компьютера.

При разработке алгоритма сначала надо продумать организацию входных и выходных данных. Один из вариантов такой организации может быть следующим.

Информация о задаче (входные данные):

1. — отрезок, на котором разыскивается решение задачи Коши, — точность расчета, 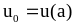—начальные условия;

2. f(x, y) — правая часть задачи (4), где , y — искомая функция (или вектор–функция в случае задачи Коши для системы ОДУ первого порядка). Для вычисления 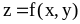, нужно написать процедуру ;

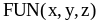3. n —максимально допустимое число членов разложения, h— минимально допустимый шаг, необходимые для достижения точности .

Результаты (выходные данные):

Для сообщения о результатах вычислений удобно ввести выходной параметр ih. Если после окончания расчета ih=0, то точность была достигнута на всем отрезке и выдается массив, содержащий n коэффициентов разложения. Если , то выдаются несколько массивов коэффициентов с указанием границ отрезков, на которых соответствующее им разложение верно с точностью . Если при минимальном шаге h или при максимальном числе членов разложения n не будет выполнено условие , то выдается информация о том, что точность не может быть достигнута.

Если написаны процедура и вспомогательная процедура , в которой вычисляется k–ая производная , то блок–схема может иметь вид, изображенный на рисунке 1. Предложенная блок– схема годится только в случае одного уравнения. При решении задачи Коши для системы дифференциальных уравнений вычисление правой части заменяется вычислением значений её компонент, а для коэффициентов разложений требуются многомерные массивы.

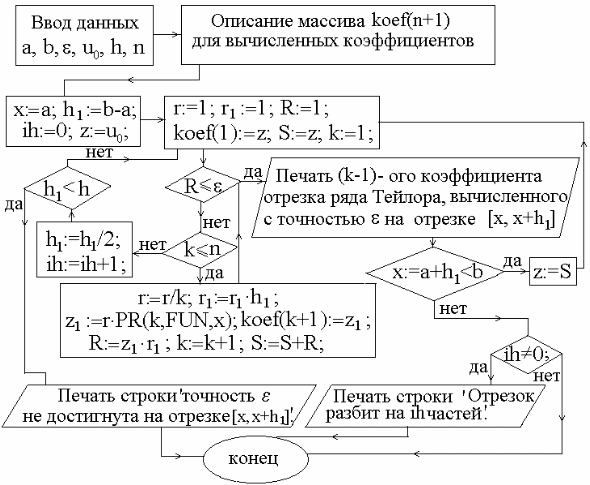
Рис. 1

Методы Рунге– Кутты

В начале 20 века Рунге, а затем Хойн и Кутта предложили подход, основанный на построении формул для численного расчета решения задачи Коши (4), не содержащих производных от функции f(x, u).

Если в некоторой точке x известно решение y(x)=u(x) задачи (4), то решение u(x+ h) разыскивается в виде

(5)

где

.

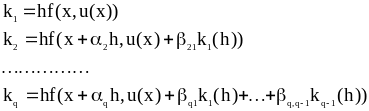Константы , и выбираются так, чтобы была мала невязка , т.е. чтобы при малых h. Так построенный метод называется явным методом Рунге– Кутты порядка s. Способ выбора констант изложен в литературе (см., например, [1] или [2]). Заметим, что знак шага h может быть любым, поэтому вычислять решение на отрезке можно, начиная с x= a, двигаясь к x= b с положительным шагом, и наоборот – двигаясь от x= b с отрицательным шагом.

Как правило, наибольшее время (наибольшее число операций) тратится на вычисление правых частей f(x, u(x)), поэтому желательно использовать расчетные формулы (5) с большим s и малым q. При q=1 существует только один метод Рунге – Кутты, который совпадает с методом Эйлера. Если , то существует семейство соответствующих методов Рунге – Кутты одинакового порядка.

Оценка погрешности.

Если в точке x известно точное решение y(x)=u(x) задачи (4), то локальная погрешность приближенного решения y(x+ h) может быть записана в виде

= ,

где s – порядок метода, C(x) зависит от значений u(x) и его производных. При малом h и достаточно гладком решении u(x) можно считать D константой. Выделение старшего члена погрешности позволяет получить приближенную оценку

Значение рассчитано по формуле (5), а вычислено по той же формуле за два шага h/2. Сначала вычисляется y(x+h/2), которое используется на втором шаге в качестве u(x+h/2) для расчета по формуле (5). Такой способ практической оценки погрешности называется правилом Рунге.

Малые локальные ошибки не гарантируют малые глобальные погрешности. Это можно увидеть, сравнивая приближенную оценку погрешности с реальной, которая вычисляется с помощью точного решения. Особенно хорошо это видно, если проводить расчет с малой точностью (с малой длиной мантиссы в операциях с плавающей запятой). Пакет Maple это позволяет. Глобальная погрешность метода зависит от свойств устойчивости задачи (4) и для неё имеется оценка

где , , C – некоторая константа, – погрешность начального условия, – вычислительная погрешность, связанная с ошибками округления.

Алгоритм расчета с автоматическим выбором.

Учитывая оценку локальной погрешности метода Рунге– Кутты s–ого порядка, начальный шаг разумно выбрать , – заданная точность расчета. Алгоритм расчета с автоматическим выбором шага начинается с вычисления решения в точке , где , и точное решение . Если

,

то шаг выбран верно, и можно продолжать расчет для , , считая с заданной точностью . Если же

, (6)

то присваивается вычисленное значение , шаг h делится пополам, повторяется расчет с новым шагом и проверяется условие (6). Деление шага продолжается до тех пор, пока не будет выполнено (6), причем делить шаг надо ограниченное число раз, так как метод Рунге– Кутты может расходиться (это может означать, что при выводе правила Рунге предположения о гладкости или другие оказались неверными). Если

,

то на этой части отрезка шаг можно удвоить. Так автоматически выбирается шаг, обеспечивающий заданную точность расчета. Как правило, шаг h<<1. Печать вычисленного приближенного решения разумно организовывать с шагом печати (например, ), то есть шаг можно удваивать, если он меньше .

Блок – схема алгоритма

метода Рунге–Кутты с автоматическим выбором шага

Входная информация о задаче может быть организована следующим образом:

1. — отрезок, на котором разыскивается решение задачи Коши;

2. — точность расчета;

3. f(x, y) — правая часть задачи (4), где , а y — искомая функция (или вектор функция в случае задачи Коши для системы дифференциальных уравнений первого порядка). Среди формальных параметров должна быть процедура для вычисления .

4. It — максимально допустимое число, указывающее сколько раз можно делить шаг пополам для достижения заданной точности (обычно It=10);

5. hp — шаг печати таблицы значений вычисленного решения;

Результаты (выходные данные):

Результаты расчета приближенного решения задачи Коши могут требоваться в различном виде. Например, требуется таблица значений решения в некоторых точках отрезка , или только значение y(b), или значение некоторого выражения, зависящего от этого решения и т.п. Для организации выдачи результатов удобно создать процедуру и объявить её формальным параметром. Процедура должна вызываться после каждого вычисленного с заданной точностью значения решения. Её формальными параметрами могут быть x – точка, в которой вычислено y= y(x), b – конец интервала, hp– шаг печати, n– порядок системы (размер массива у), – признак: если ipr=0, то надо продолжать счет, а если — прекратить.

Пусть написаны процедуры , и вспомогательная процедура , в которой вычисляется значение приближенного решения по известному и по выбранной формуле Рунге–Кутты. Тогда блок– схема метода Рунге–Кутты с автоматическим выбором шага может иметь вид, изображенный на Рис.2.

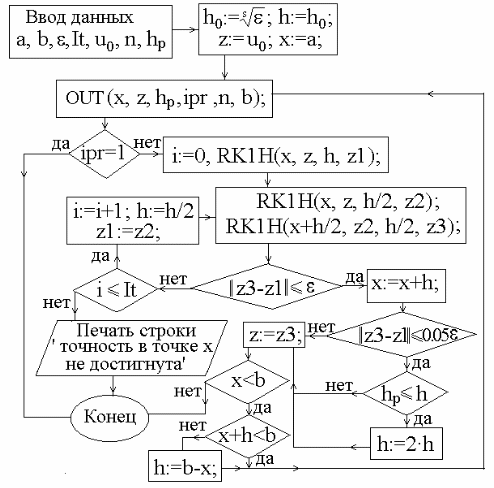
Рис.2.

Вложенные формулы Рунге– Кутты.

С 1957 года появились формулы Рунге–Кутты, с помощью которых можно вычислить приближенные значения и разных порядков точности. Сначала строился метод р– ого порядка

с таким набором коэффициентов , что

.

Далее выбирались коэффициенты так, чтобы при тех же значениях формула Рунге–Кутты

,

имела погрешность порядка ( обычно )

.

Один из этих методов получается как «побочный продукт» при построении другого. Тогда имеем

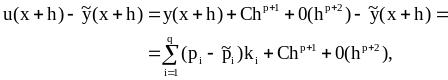
и для практической оценки погрешности получается выражение

Построенные таким образом вложенные методы позволяют уменьшить число необходимых операций для вычисления практической оценки погрешности. Заметим, что эти методы называются “фамилия автора p(s)”, где p означает порядок , а s – порядок , причем произвольные постоянные в формулах Рунге-Кутты выбираются так, чтобы минимизировать коэффициенты в выражении для погрешности результатов с порядком p.

В качестве примера вложенного метода приведем наиболее используемый в настоящее время метод Фельберга 4(5)

,

,

где

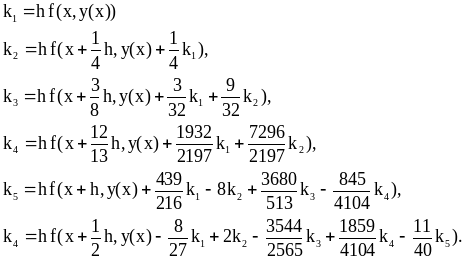
Блок схема для вложенных методов проще предложенной выше, напишите её сами. Во вспомогательной процедуре удобно по выбранной формуле и известному вычислять значение приближенного решения вместе с его погрешностью .