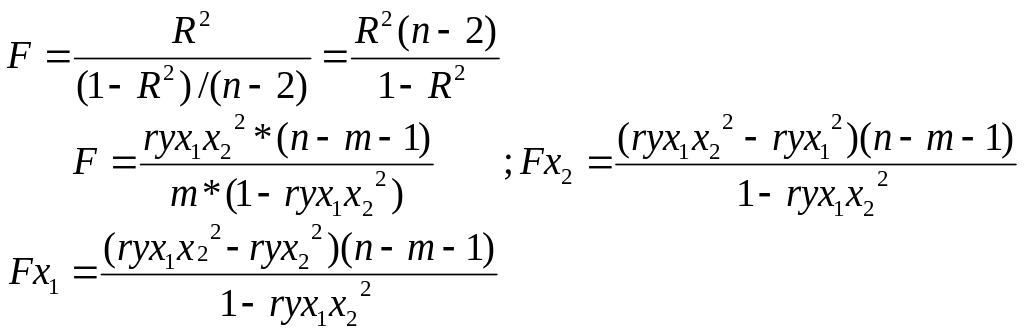І және іі түрдегі қателер.

Регрессиялық талдау жүргізгенде гипотезаны тексеру барысында І,ІІ жақты критерийлер қарастырылады. Тексерілетін гипотеза Но: белгіленіп, нөлдік гипотеза деп аталады. Нөлдік гипотезамен қатар, оған қарама-қарсы альтернативті Н1: гипотеза қарастырылады. Но: Екі мүмкін болатын таңдауды білдіреді. Но: қабылдау немесе қабылданбау білдіретін ереже- статистикалық критерий деп аталады. а- мәндік деңгейін беріп в-ның мәнін в1 сол жағы, в2 оң жағы жату ықтималдылығы а болатындай во қатысты симметриялы [в1;в2] интервалын құрайды. а әдетте, 1% немесе 5% алынады. Егер Но: орындалса, в во манайында жатады, яғни [в1;в2] интервалына тиісті. 2 мүмкін жағдай: 1)қабылданады 2)интервалдвн тыс жатса, Но: қабылданбайды. Гипотезаны тексеру барысында қателер: Ақиқат Но: қабылданбауы 1-реттік қатеге әкеледі. Жалған Но: қабылдасақ 2-реттік қате орын алады.

	Ақиқат	Жалған
Қабылданады	Дұрыс	2-реттік
Қабылданбайды	1-реттік	Дұрыс

Көптiк регрессия теңдеуi және оның матрицалық жазылуы.

Кез келген әкономикалық көрсеткішке бір ғана емес, көбінесе бірнеше факторлар әсер етеді. Мысалы, кейбір тауарға сұраныс тауар бағасымен ғана емес, басқа оны алмастыратын және толықтыратын тауарлармен, тұтынушы табысымен және көптеген басқа факторлармен анықталады. Бұл жағдайда екі айнымалының сызықтық регрессиясының заңды жалғасы - көптік регрессия моделі қарастырылады:

уі- тәуелді айнымалы (предикатор) - і-ші бақылаудың қорытынды белігісінің мәні; хji - і-ші бақылауға сәйкес j-ші фактордың мәні (тәуелсіз немесе түсіндіруші айнымалы) ( j = 1,2,...,m);

i- і-ші бақылауға сәйкес қорытынды белгінің кездейсоқ құраушысы; βо- бос мүше, ол х1 = х2 = ... = хn =0 болғандағы у-тің формальды мәнін көрсетеді. βі, і = 1,2,...,к параметрлері, егер i-ші тәуелсіз айнымалылары 1-ге өскенде, тәуелді айнымалы орташа қанша бірлікке өскендігін көрсетеді. Тәуелсіз айнымалылар кездейсоқ шамалар емес, ал тәуелді айнымалы шама - кездейсоқ, шама себебі оның құрамына кездейсоқ шамалар кіреді. Байланыс моделі ретінде сызықты функцияны таңдап алғаннан кейін, регрессия параметрлерін бағалау қажет. х = (х1, х2,..., хn) түсіндіруші векторының n бақылауы және Ү тәуелді айнымалысы берілсін делік: (хі1,хі2...,хim,уi), і = 1,2,...,n. β0,βІ...,βn параметрлерін есептеу есебін бір мәнді түрде анықтау үшін (яғни кейбір ең жақын β векторын табу) n≥m+1 теңсіздіктің орындалуы міндетті. Егер бұл теңсіздік орындалмаса, параметрлердің мәндеріне көптеген әртүрлі векторлар сәйкес келеді. Бұл жағдайда X пен Ү арасындағы байланыс бар бақылауларға дәлме-дәл сәйкес келеді. Бұл жағдайда, егер n=√m+1 болса, онда β векторының коэффициенттері бір ғана жолмен - m+1 сызықты теңдеулер жүйесі арқылы есептеледі:

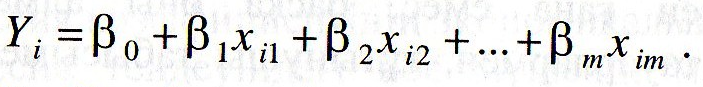
Матрицалық жазылуы:

Бағалардың ығыспағандығы,  тиiмдiлiгi және орнықтылығы.

Кездейсоқ шама сипаттамасының бағасы ығыспаған деп аталады,егер оның математикалық үміті осы сипаттаманың ақиқат мәніне тең болса.Мысалы, μ математикалық үміттің бағасы ретінде таңдамалы орташа алынсын. Таңдама элементтері бас жиынтықтан кездейсоқ түрде алынатындықтан, олардың әрқайсысы үміт қасиеттерінен алатынымыз демек таңдамалы орташа математикалық үміт үшін ығыспаған баға болып табылады.

Параметрдің ығыспаған бағасы тек қана біреу болмауы мүмкін. Осы параметрдің барлық ығыспаған бағалары ішіндегі дисперсиясы ең кіші болатын баға тиімді деп аталады.

Мысалы үшін таңдамалы орташа μ математикалық үміттің тиімді бағасы болып табылатынын көрсетсем. Сонымен қатар кез келген басқа сызықтық ығыспаған бағаны қарастырам:

Кездейсоқ шаманың ықтималдық бойынша шегі сипаттамасының ақиқат мәніне тең болса, онда осы сипаттама бағасы орнықты деп аталады.

Мысалы, X1,X2,...,Xn таңдаманың орташасы үшін таңдамалы орташаның дисперсиясы нөлге ұмтылады. n таңдама өлшемі өскен сайын мәні μ математикалық үмітке барынша жақындай түседі, яғни бағасы μ мәніне ықтималдық бойынша жинақталады: p lim =μ.

Теңдеудің жалпы сапасын тексеру.

Гипотезаны тексеру үшін Фишердің F-статистикасы қолданылады. Fстат.= R²/k / (1-R²)/(n-k-1) яғни, жұптық регрессия үшін Fстат.=R²/1-R². Fкрит. мәні тәуелсіз айнымалылар саны мен еркіндік дәреже санына байланысты. k- тәуелсіз айнымалылар саны, n-k-1- еркіндік дәреже саны. Fстат.<Fкр. болса, Но: қабылданады, R²-мәнсіз. Fстат.>Fкр. болса, Но: қабылданбайды, R²- мәнді, сенімді және сапасы жақсы.