1	Теоретикалық және таңдамалы мiнездемелер.
2	I-шi реттi қалдық автокорреляциясы оны анықтау жолдары
3	Гетероскедастикалық және оны анықтау жолдары
4	Мультиколлинеарлық құбылыс. Жорамал айнымалылар.
5	Детерминация коэффициентi. Түзетiлген детерминация коэффициентi.
6	Нүктелiк және интервалдық бағалар.
7	Модельдер спецификациясы
8	Теңдеудің жалпы сапасын тексеру.
9	I және II реттi қателер.
10	Бағалардың ығыспағандығы,  тиiмдiлiгi және орнықтылығы.
11	Көптiк регрессия теңдеуi және оның матрицалық жазылуы.
12	Регрессия теңдеуiнiң коэффициенттерiн есептеу үшiн кiшi квадраттар әдiсi.
13	Көптiк сызықты регрессияның классикалық моделi.
14	Гаусс-Марков шарттары
15	Регрессия коэффициенттерiнiң бағасының мәнділігін талдау.

Теоретикалық және таңдаулы мiнездемелер.

Таңдамалы сипаттамалар: Таңдамалы ковариация – екі айнымалы арасындағы байланысты көрсетеді және келесі формулалармен анықталады:

cov>0 болса айнымалылар арасында оң байланыс болады, cov<0 болса айнымалылар арасында теріс байланыс болады. cov=0болса, онда байланыс жоқ болады.

Таңдамалы ковариация қасиеттері: 1)y=u+v; Cov(x,y)=Cov(x,u)+Cov(x,v); 2)y=a*u; a=const; Cov(x,y)=a*Cov(x,u); 3)y=a; Cov(x,y)=0. Теоретикалық коварация:

Таңдамалы дисперсия: Cov(x,y)=Var(x).

Таңдамалы дисперсия қасиеттері: 1)y=u+v; Var(y)=Var(u)+Var(v)+2Cov(u,v); 2)y=a*u; a=const; Var(y)=a²Var(u); 3) y=a; Var(y)=0 4)y=u+a; Var(y)=Var(u). Таңдамалы корреляция қасиеті екі айналым арасындағы байланыс тығыздығын көрсетеді. rxy [-1;1]. rxy→1 айнымалылар арасында тығыз оң байланыс бар, rxy→-1 айнымалылар арасында тығыз теріс байланыс бар. rxy →0 айнымалылар арасында байланыс жоқ. Теоретикалық коррелляция:

Бірінші ретті қалдық автокорреляциясы оны анықтау жолдары

Бірінші ретті автокорреляция коэффиценті - бұл лагтары бар қалдықтардың таңдамалы корреляция коэффиценті, яғни:

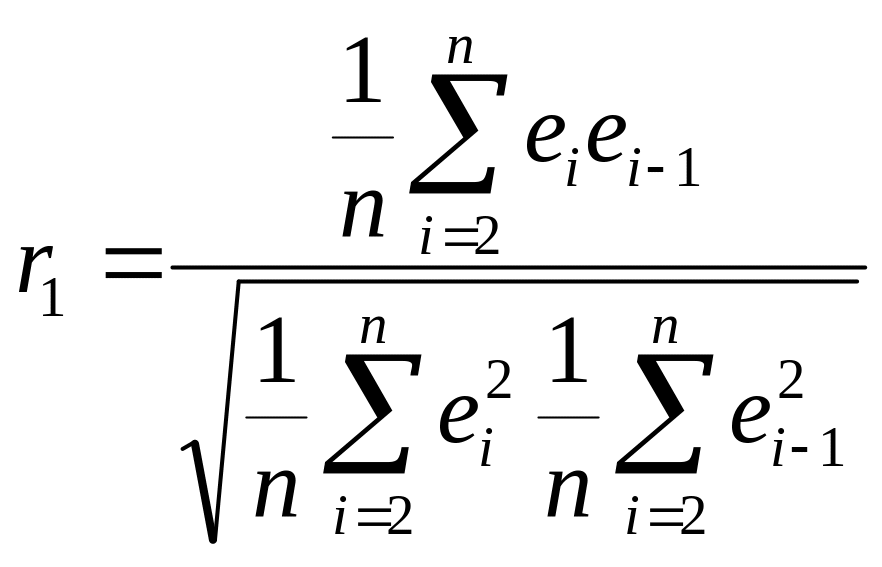
(Мұндағы және үшін таңдамалы орташалары салыстырмалы аз және ыңғайлылық үшін қарастырылмайды).

Болғандықтан, бірінші ретті автокорреляция коэффиценті

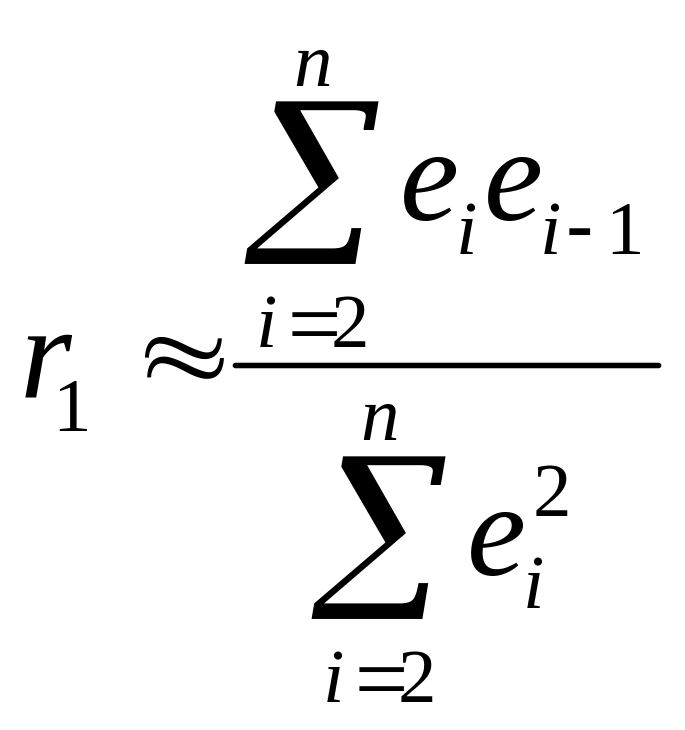
Автокорреляцияны анықтау үшін әдетте Дарбин-Уотсон статистикасы қолданылады:

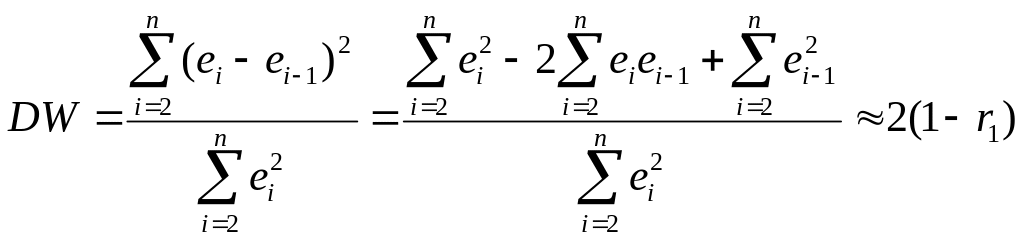
Автокорреляция оң болғанда , яғни оған сәйкес келеді. Теріс автокорреляция кезінде , онда . Автокорреляция жоқ болғанда , сондықтан Дарбин-Уотсон статистикасы .

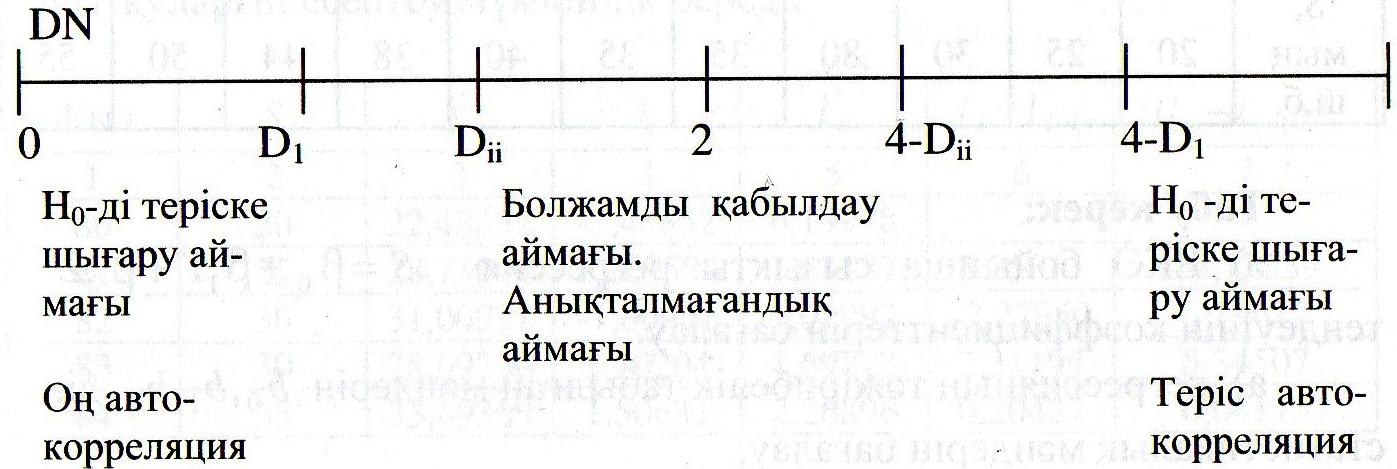
Дарбин-Уотсон статистикасы тек түсіндіруші айнымалылар санынан ғана емес, олардың таңдамадағы қабылдайтын мәндеріне де байланысты болады. Сандықтан t-статистика және F-статистикамен салыстырғанда Дарбин-Уотсон статистикасының критикалық мәндерінің кестесін құруға болмайды. Бірақ үшін жоғары және төменгі шекараларын анықтауға болады. Оларды кесте арқылы табамыз.

Нөлдік және альтернативті гипотезалар ұсынылған: оң автокорреляция жоқ,

оң автокорреляция бар. Егер DW< болса, онда DW<, және гипотезасы қабылданбайды, яғни есебінен оң автокорреляция бар дер қорытынды жасауға болады. Егер DW> болса, DW> ақиқат және гипотеза қабылданады, оң автокорреляция жоқ деген қорытынды жасалады.

Ал ≤ DW ≤ болған жағдайда, DW мен мәндерін салыстыру мүмкін емес және оң автокорреляция бар және жоқ болуы жайлы анық ештеңе айта алмаймыз. (,) интервалы - анықталмаған зона болады. Теріс автокорреляция болуын тексеру де осы жолмен жүзеге асады.

Гетероскедастикалық және оны анықтау жолдары

Гетероскедастикалық құбылыс кездейсоқ мүшенің дисперсиясы байқау саны өзгерген сайын ерекшеленген жағдайда орын алады. Гетероскедастика жағдайында регрессия коэффициенттері ығыспаған, бірақ тиімсіз болады. Гетероскедастикалық құбылыстың математикалық түрде анықталуы: .

Гетероскедастикалықты анықтаудың түрлі әдістері бар. Голдфелд-Кванд тестінде , байқау өсуі бойынша реттелінеді. Алғашқы n’ және соңғы n’ байқаулар алынады да, олар үшін жеке регрессиялар құрылады және және қалдықтар квадраттарының қосындылары бағаланады. Келесі қатынас анықталады:

～F(n’-k, n’-k) мұндағы k- бастапқы регрессия теңдеуінің параметрлерінің саны. n’ шамасын жуықпен -ге тең деп алуға болады. Гетероскедастикалықтың жоқтығы жайлы келесі нөлдік гипотеза тексеріледі:

Егер / қатынас Фишердің үлестірілуінің критикалық мәннен асса, δ мәнділік деңгейінің таңдалған критикалық мәні үшін гипотезасы жоққа шығарылып, гетероскедастикалықтың бар болуы жайлы гипотеза қабылданады. Тәжірибеден бұрын құрылымдық шектеулерге негізделген басқа да тесттердің арасынан Спирменнің рангтік корреляция тесті жәге Глейзер тестін атап көрсетуге болады.

Уайт(White) тесті гетероскедастиканың құрылымы жайлы қандай да болмасын жорамалдар жасамайды. Бұл оның әмбебаптығын көрсетеді. Бұл тест, егер гетероскедастикалық бар болса, қателердің дисперсиясы регрессорларға, олардың квадраттары және жұптық көбейтінділеріне тәуелді деген пікірге негізделеді. Қателердің дисперсиясы белгісіз болғандықтан, регрессияда олардың орнына қалдық квадраттары алынады.

Жоғарыдағы гипотеза қабылданса келесі шарт асимптотикалық орын алатыны дәлелденген ～ мұндағы: - детерминация коэффиценті, m -қалдық квадраттары үшін теңдеудегі регрессорлардың саны. Уайт тестін EVIEWS эконометрикалық пакеті арқылы жүзеге асыруға болады.